We’ve looked at how to find the circumference of the earth, and how far we can see over the horizon. Another kind of question we’ve had about the curvature of the earth is, how much does it curve over a given distance? That has been asked in several different ways, which lead to some intriguing insights.
How high a bulge?
Here’s the first question, from 1997:
Earth's Curvature I am interested in knowing the degree of curvature of the earth's surface. I am attempting to find a method which would allow me to conceptualize and calculate the making of such a depiction on paper. That is to say, if the earth curves from point A to point B, points exactly 10 kilometers apart, if one were to draw a straight line between the two points, then WHAT WOULD BE THE HEIGHT of the highest point the curvature AB would be above the line AB? Moreover, if the point AB were now to be 20 kilometers apart, would the height be 2 times the height calculated earlier or would it be something altogether different? Thank you for your kind consideration and aid. This young artist sincerely and surely appreciates it!
Curvature is technically measured in terms of the angular turn per unit distance, in various ways; as we’ll see throughout this post, trying to measure it in terms of distances only, while it seems to be a natural idea, causes some trouble. But the second question here, about how things change when you double the distance, is just the insight we’ll need at the end.
Doctor Lorenzo answered:
Hi Neha - The first thing to realize is that this problem is about circles in the plane, not about spheres in 3-dimensional space. You are only interested in comparing a curve and a straight line, and they all lie in the same plane. A plane through a sphere yields a circle. So we just have to understand how a circle pulls away from a straight line.
Here’s what that cross-section looks like (exaggerated as usual) as he’ll set it up in a coordinate system:
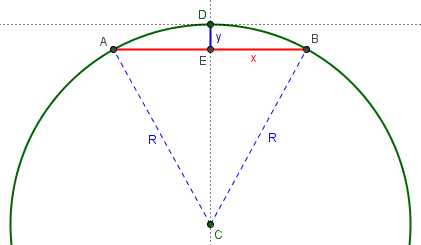
Consider a circle of radius R, tangent to the x-axis at the origin and the center on the negative y-axis. (I set it up this way in order to simplify the calculation of the height which now will go straight up the y-axis from the midpoint of line AB to the origin.) The equation for such a circle is: x^2 + (y+R)^2 = R^2 Equivalently, x^2 + y^2 + 2Ry = 0 Equivalently, y = -(x^2 + y^2)/(2R)
He is using an unconventional trick here; note that he didn’t really solve for y, which is still on both sides of the equation, but that will disappear into an approximation:
Near the origin y is small, and y^2 is smaller still, so this can be approximated by: y = - x^2 / (2R) If 2 points are separated by a distance L, they might be point A at x = -L/2 and point B at x = +L/2. At both A and B we have: y = - L^2 / (8R) That is, while the curve from A to B goes through the origin, the straight line from A to B cuts a distance L^2/(8R) below the origin. Notice that doubling L (say, from 10 miles to 20) means quadrupling this distance.
Here is a picture showing the new labels:
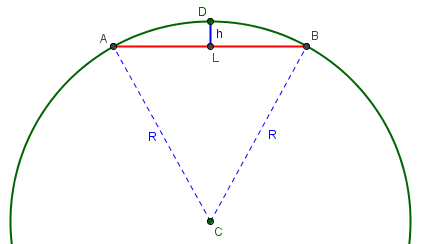
When two points A and B are L units apart (“as the mole digs”, one might say), the straight line joining them is \(h \approx \frac{L^2}{8R}\) below the surface at its midpoint. Keep in mind that this is approximate, applicable only when L (and therefore h) is much less than R.
As for the curvature of the actual earth, you just have to plug in, for R, the radius of the earth, which is about 4000 miles. So, if L = 10 miles, then: y = (100/32,000) miles (about 16 feet)
As we should expect, this is not a very high pile of earth, for distances at this scale; drawings such as ours above have to show huge distances to make the curve even visible.
You can see this effect in real life. If you look across a 10-mile wide lake at the other shore, you can't see the low buildings on the other side! To see a cabin 16 feet high, you would have to climb a ladder so that your eyes are 16 feet above the ground (to be exact you would take into account the effect of the curvature on the angles of the building and your viewing station make relative to the "y-axis", but this effect is negligible at this distance). This is dramatic in Lake Tahoe, where, from the north shore of the lake you can see the tall casinos of Stateline, Nevada, but not the low buildings of South Lake Tahoe, California. (Lake Tahoe is also more than 10 miles from top to bottom).
Relating this bulge to the line of sight we looked at last time, we see that two points 10 miles apart would have to be 16 feet above the water level to (barely) see each other.
By the way, the L^2/(8R) answer is only an approximation, since we ignored the y^2 term in the equation of the circle, and ignored the difference between the straight-line distance between A and B and the distance along the curve. These corrections are negligible, being approximately of size L^4/R^3. If L = 10 miles and R = 4000 miles, these corrections add up to less than 1/1000 of an inch!
We’ll see an exact formula next.
Improving accuracy
In 2004, a student tried out the formula, not on the earth but on a drawn circle, and his question was added to that page (with wording changed accordingly):
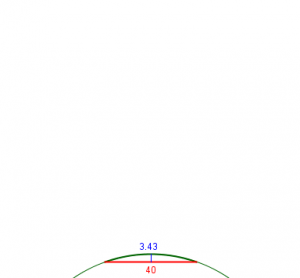
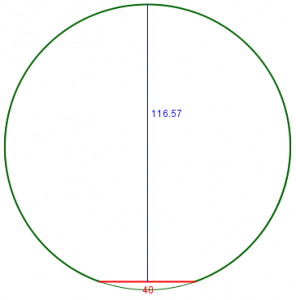
Your reply to this question assures us that the Math is the same for all the calculations and the only things that change are the radius of the circle and the distance from a to b. I have drawn a circle with a 60 mm radius and tried out the calculations. Where "L" (distance between points a and b) is very short, say 40 mm, then the result "Y" is virtually accurate. However, as you lengthen "L" to say 115 mm the result "Y" becomes wholly inaccurate. Instead of a measured result of 42 mm the calculation result is 27 mm. Can you shed any light on this for me please? Am I missing something very simple?
Here is the circle with Martin’s two chords and actual measurements:
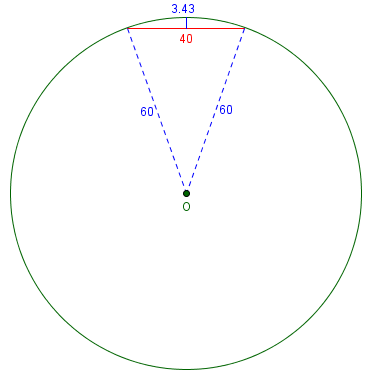
$$h \approx \frac{L^2}{8R} = \frac{40^2}{8\cdot 60} = 3.33$$
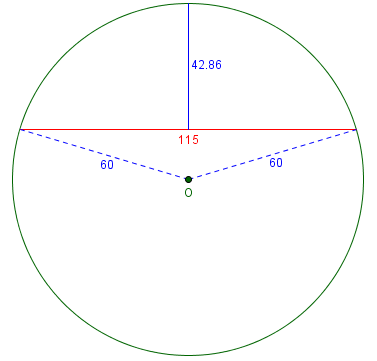
$$h \approx \frac{L^2}{8R} = \frac{115^2}{8\cdot 60} = 27.55$$
Doctor Vogler replied:
Hi Martin, Thanks for writing to Dr Math. The last paragraph in the reply reads: By the way, the L^2/(8R) answer is only an approximation, since we ignored the y^2 term in the equation of the circle, and ignored the difference between the straight-line distance between A and B and the distance along the curve. These corrections are negligible, being approximately of size L^4/R^3. If L = 10 miles and R = 4000 miles, these corrections add up to less than 1/1000 of an inch! So essentially he is saying that when L is small compared to R, then the approximation is very good. In your example, L is not small compared to R; in fact, L is bigger than R.
The formula is, in fact, working as advertised. And the approximation is appropriate for human distances on the earth. But what if we want to handle small circles and big chords?
So let's get a more exact result. You'll recall that the approximation was in neglecting the y^2 term in x^2 + y^2 + 2Ry = 0. So what happens if we DON'T neglect the y^2 term? Then when we substitute x = L/2, we get y^2 + (2R)y + (L/2)^2 = 0 and we solve for y using the quadratic formula: y = -R + (1/2)sqrt(4R^2 - L^2) and y = -R - (1/2)sqrt(4R^2 - L^2), and then the height to the x axis would be -y = R - (1/2)sqrt(4R^2 - L^2) or -y = R + (1/2)sqrt(4R^2 - L^2),
Note that \(-y\) is our h; he’s made it positive.
If you look on the circle, you notice that one of these answers is measuring the height where the curved line around the circle takes the shorter way around the circle (that's the first answer) and the other gives the answer if the curved line takes the long way around the circle.
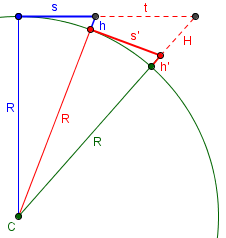
Here are the two solutions:
The exact formula gives, respectively, $$h = R – \frac{1}{2}\sqrt{4R^2 – L^2} = 60 – \frac{1}{2}\sqrt{4\cdot 60^2 – 40^2} = 3.431$$ and $$h = R – \frac{1}{2}\sqrt{4R^2 – L^2} = 60 + \frac{1}{2}\sqrt{4\cdot 60^2 – 40^2} = 116.569$$
In the archived answer, he was looking for the short way, and you'll find that if L is small compared to R then the square root can be approximated by two terms of the Taylor series, sqrt(4R^2 - L^2) is about 2R(1 - (1/2)(L/2R)^2) where the difference will be roughly the size of the third term of the Taylor series, which is (1/8)(L/2R)^4. That approximation gives the same answer as recorded in the archive, L^2/8R. But if (L/2R)^4 is not a small number, then this is certainly not a good approximation, and so you should use the exact answer, R - (1/2)sqrt(4R^2 - L^2).
This is an alternative way to obtain the approximation, and is also the source for the estimate of the error, “being approximately of size L^4/R^3”.
Martin answered,
Thank you very much. Works a treat. Faith in math restored.
How fast a drop-off?
A different perspective was taken by James in 2003, who referred back to that answer:
Earth's Curvature My son and I wondered what would happen if there were no gravity. I jokingly said that you'd take a step and simply float in a straight line forever. That got me to thinking: How far would you have to "walk" this way to get 1 foot off the ground? Scientifically, how far would you have to follow a tangent of the earth to be one foot above the surface of the curvature? Could you use triangulation somehow? Could you use the formula for a circle to calculate the slope? In another discussion: Earth's Curvature http://mathforum.org/library/drmath/view/54904.html you say that the formula for a circle is x^2 + (y+R)^2 = R^2 and that, "if 2 points are separated by a distance L, they might be point A at x = -L/2 and point B at x = +L/2. At both A and B we have: y = - L^2 / (8R)" That leads me off in the general direction, but I'm not finishing the connection.
Doctor Jeremiah had an answer, which is closely tied to our horizon questions from last time:
Hi James,
Imagine a perfectly spherical world with a tangent:
A B
+++++ -------+
+++ | +++ /
+++ | +++
+ | / +
+ | / +
+ | / +
+ R R+1 +
+ | / +
+ | / +
+ | / +
+ |/ +
+ + +
You travel from A to B. Your distance from the center of the Earth at A is R, and your distance from the center of the Earth at B is R+1. This is a simple right angle triangle and can be solved for the distance from A to B with the Pythagorean formula:
(R+1)^2 = R^2 + d^2 where d = the distance from A to B
d^2 = (R+1)^2 - R^2
d^2 = R^2+2R+1 - R^2
d^2 = 2R+1
d = sqrt(2R+1)
This is the distance to the horizon from point B, which is 1 unit above the surface.
The radius of the Earth (R) is 3963.19 statute miles or, more importantly for us, 20925643.2 feet. That means:
d = sqrt(2R+1) where R = 20925643.2 feet
d = sqrt(2*20925643.2+1)
d = sqrt(41851287.4)
d = 6469.26 feet
So you would have to travel along the tangent for over a mile to get one foot off the ground.
We’ll connect this to the bulge formula soon!
8 inches per mile?
I want to include an example of a question we got several times, that was never archived. This is from 2009:
Hi, I've read that the curvature of the earth is approximately eight inches per mile. Here's the problem. If it only curves eight inches per mile, that doesn't seem to be nearly enough to explain things we know about our planet. E.g. sailors can observe ships disappear over the horizon, but if the curvature is only eight inches per mile, then 20 miles (which is the furthest you can see a ship with the naked eye) would only give a curvature of 160 inches, or approximately 13 ft - nowhere near enough for a ship to disappear. More strikingly, at 4000 miles (approximately the radius of the planet) you would have a curvature of less than a mile. Again, that seems far too small a number. I must be missing something but I can't figure out what it is. I'm guessing that the curvature does not merely add up in a linear fashion, e.g. if it has deviated eight inches after one mile it is not correct to assume that it has deviated sixteen inches after two miles. Perhaps the curvature grows in an exponential fashion? But I'm clutching at straws here because, frankly, I'm totally confused!
That was a pretty good guess; in fact, if you’ve been reading observantly, you will have seen a partial answer very similar to his suggestion.
I answered:
That's exactly it (though not literally exponential, as we'll see). It's not appropriate to state the curvature as "8 inches PER mile", because the word "per" implies a proportionality, which is not true here. The earth presumably does curve down 8 inches in each mile, but since the direction of "down" keeps changing, they don't add up so that it goes down 8d inches in d miles. All you should say is that it goes down 8 inches in ONE mile.
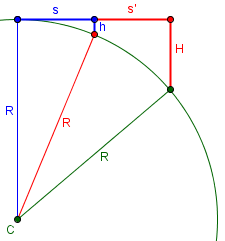
Here is what I mean:
If the drop of the earth over the first mile, h, is 8 inches, then if we dropped to the ground and continued another mile, we would have another drop, h‘, of 8 inches. But that mile would not be in the same direction, nor would the drop at its end. If we actually continued in the same straight line, we would have a considerably longer drop, H.
Let's look at specifics. If we were to graph a cross-section of the earth, life-size, with our location at the origin and the center below us on the y axis, the center would be at about -4000 miles, or -21,120,000 feet, or 253,440,000 inches, on the y-axis. The equation of this circle would be x^2 + (y + r)^2 = r^2 Solving for y, y = sqrt(r^2 - x^2) - r
This is the drop perpendicular to our straight line, not perpendicular to the earth, which has curved away under us:
Clearly, the drop is not just twice h. For the much smaller size we are discussing, the difference will not be so great, but it will still be real.
To check your claim, we can find y when x = 5280*12 = 63360 inches:
y = sqrt(253,440,000^2 - 63360^2) - 253,440,000
= -7.92 in
So the circle does indeed go down about 8 inches in a mile.
This is about what we found before, but is in a different direction this time, so it is a little more.
Let's repeat the process for 2, 3, 4, ... miles out. I'll use a spreadsheet to do it.
X Y
63,360 -7.92 (at 1 mile)
126,720 -31.68
190,080 -71.28
253,440 -126.72
316,800 -198.00
380,160 -285.12
443,520 -388.08
506,880 -506.88
570,240 -641.52
633,600 -792.00 (at 10 miles)
6,336,000 -79,212.38 (at 100 miles)
So in 10 miles the earth drops not 80 inches, but almost 800 inches, or 66 feet -- so it's nearly quadratic (proportional to the square of the distance), which can be explained with a little more algebra. At 100 miles it's dropped 6600 feet, over a mile.
That starts to make a little more sense!
Chris responded with a couple other references:
Many thanks for a superbly comprehensive and informative answer. I really appreciate you taking the trouble. I note that I'm not the only person who was confused about the problem; if you google 'curvature earth' the first hit you get takes you to a maths discussion page not unlike Dr Math, but the answer provided makes the wrong assumption that you corrected in your answer (namely that the earth curves eight inches PER mile, therefore 80 inches for ten miles etc). A later poster corrected this misconception but it's obviously widespread! If you're interested you can find it at http://mathcentral.uregina.ca/QQ/database/QQ.09.02/shirley3.html One of your colleagues at Dr Math does a better job but still comes up with a different figure for how much curvature there would be at 10 miles (he reckons 16 ft rather than 66 ft). http://mathforum.org/library/drmath/view/54904.html Anyway, either way you have done a great job of illuminating this point, and I'm very grateful for the clarity of your explanation and the amount of detail you went into. I hope you have a great weekend - as far as I'm concerned you've earned it!
Here is part of the MathCentral page:
[Question:]
There are 2 six foot men. What would the distance be between them before one could not be seen because of the curvature of the earth?
My grandson, who is stationed in Baghdad, Iraq, asked the question. This is one of the fun problems his unit was discussing. Thanks for your time.
[Original answer:]
In an earlier question on the curvature of the Earth Harley showed that the earth curves approximately 8 inches per mile. Since 6 feet is 72 inches and 9*8 = 72, the Earth curves approximately 6 feet in 9 miles. Thus the two men would have to be approximately 18 miles apart.
This answer was corrected in 2004, by finding each man’s distance to the horizon as about 3 miles, so that the correct answer is about 6 miles, not 18. If we use the approximately quadratic nature of the relationship, we might estimate that the earth will drop 9 times as much in about \(\sqrt{9} = 3\) times as far, so, again, each man walks 3 miles and their total distance is 6 miles.
I replied first to the MathCentral error:
It's an easy thing to do if you don't think carefully!
(By the way, Ask Dr. Math has been known to make errors too. We’ve even made a couple minor errors in our current incarnation as The Math Doctors …)
Then, to the apparent discrepancy in our previous answer, which was the first answer in this post:
I think he does a great job; he filled in what I skipped over by saying "... which can be explained with a little more algebra". As for the numerical discrepancy, he isn't dealing with the amount of dip in 10 miles, but the amount of rise BETWEEN two points 10 miles apart, which (as mentioned in the other page) is equivalent to the amount of dip in only 5 miles. My table shows a dip of 198 inches, or 16.5 feet. So he's got it just right.
It’s definitely a mind-bending problem!
Hi,
I am trying to link the derived equation y = sqrt ( r^2 – x^2 ) – r to a sketch.
I cannot figure it out with the sketch provided below the derivation. That’s where you move the centre and location of the circle. I’d like to have my facts straight when debating the flat earth.
Thank you.
You’re referring to the last section, “8 inches per mile?” It’s unfortunate that I labeled the picture below that equation according to my previous picture, rather than the equation itself. Here is a picture that should be clearer, showing that x is what was called s, and y is the negative of what was called h, since the point below is (x, y) = (s, -h).
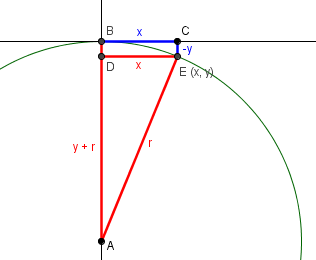
The derivation doesn’t require the picture; we wrote the equation of the circle, whose center is (0, -r), as x^2 + (y + r)^2 = r^2, and then solved for y: subtract x^2 from both sides to get (y + r)^2 = r^2 – x^2, then take the square root and subtract r. The result, y, is the negative of the distance fallen. If you don’t want to use the equation of the circle, you can apply the Pythagorean Theorem to the right triangle in red. (The vertical side could have been called r-h.)
Pingback: A Tunnel Through the Earth – The Math Doctors
I would just like to pose a query. If you say that seeing across Lake Tahoe is evidence of the size of the earth being so large we don’t perceptually see curvature, then I would ask to know how far would we see if there were wasn’t any curve?
Also if we are measuring the “rise” of one point from another and not the “dip”, then what if we saw that same point, say 20 miles away? Would it still be the “rise” between that point and the point of the observer..?
And lastly, what if you were in fact lied to about the *shape of the earth? And how would you know if you were or weren’t? You’re move.
The point about Lake Tahoe is not that the earth is so large, but that it is small enough that it curves enough to observe over such a small distance. If the earth were really large, it would be relatively flat, and you could see farther.
If the earth weren’t curved, then we could conceptually see forever (over water), because the straight line to anything would be entirely above the surface. We could not only see the feet of someone on the opposite shore (as opposed to the tops of buildings); we could see the Alps from Boston. Of course, haze and refraction would eventually get in the way.
“Rise” and “dip” are just different perspectives on the same thing. I don’t know what your point is.
As for being lied to, that cuts both ways. You have to look at the evidence, and decide what explanation fits all of it.
Hey Brian
Why is it here in Australia the moon appears to be upside down to what it appears in say, America or anywhere in the northern hemisphere? Bit weird don’t you think?
Also explain how catching a plane from Sydney Australia to Chile South America is 12 hours 20 minutes? Using your version of the world map I would cross several other countries or take double the time. Just trying to get that whole scale thing right. I’m sure you have the math and equations ready to go for us to all double check and agree.
Because this post is not about whether the earth is round, but about calculations, I don’t normally permit comments that just argue about the former. I’ve approved this just to make that point, and to refer to an earlier post that comes a little closer to this topic: Proving the Earth is Round … or Not. There I talked about Eratosthenes’ measurement of the earth, and pointed out that, in itself, that does not prove anything, since the one measurement could be explained on a flat-earth basis. But at the end, I said,
“Now, if you gathered additional data from different locations, you’d start finding inconsistencies with this model; at the extreme, if you could go 6000 or so miles to the north (to the north pole), you’d find that on the same day, angle A is 90°, and H would become 0.
“But the flat earth model was known to be wrong long before anyone traveled that far.”
Observations from the other side of the world, and from traveling there, are another example of “additional data”. It is from looking at all the data, not just one observation, that one can be convinced. The appearance of the moon in Australia, alone, probably could be explained in some flat-earth model, but it would conflict with other facts.
The waters are full of mud. I wonder why?
Super easy formula for this:
miles squared * 8 inches
For example, 3 miles squared = 9 * 8 = 72 inches … 6 ft drop in 3 miles which under the most basic of observations makes absolutely no sense… thus the mud in the water.
Hi, Jason.
Your formula agrees with what we say here, that the drop is approximately 8 inches at one mile, and approximately proportional to the square of the distance. And we show above that at 3 miles (190,080 inches), the drop is about 71.28 inches, or 6 feet, just as you say. So nothing you say is a surprise.
This also agrees with what we say in the companion post, How Far Can I See?, that the horizon is about 3 miles away if your eyes are 6 feet above water level: If you can just see the feet of a person on shore 3 miles away, so that your eyes are on the horizontal line skimming the water from those feet, then the water at your feet is 6 feet below that horizontal line. The water surface has dropped 6 feet in those 3 miles.
If you have no experience with such a drop, then try it out (from a boat, or across a river or lake). Many people don’t pay attention to what they see (or misunderstand what they are told about the horizon). But if these things weren’t true, then I could see Canada across Lake Ontario from where I live; instead, the lake “bulges up” between the shores, just as we expect.
I think the Squared part of this equation gets people tripped up. When have you ever said, Oh I’m going to my friends house, he lives 10miles Squared away from here. Anything squared is a measurement of Area. Not a measurement of distance. Now I bet if we did a calculation in Linear Feet (Wink wink) we would have an answer more proportional to our expectations.
And you CANNOT ignore refraction. Light travels differently through different elements or densities. Evident by trying to catch a fish with a spear, or Skuba divers change in depth perception; the observer’s interpretation is skewed to what is actually -objectively- occurring.
And you have to also consider Gravity’s affect on photons. Evidenced by black holes or time-space distortions. While I agree that photons have no measurable resting mass, they do have a mass! And anything with mass gets affected by gravity!
In conclusion, factor in gravity, refraction, and possibly more factors like heat (looking through the exhaust of an airplane, the image gets distorted) and think of any errors and geometric progression and you have a huge discrepancy.
Hi, Flash.
I’m not sure what point you are making; perhaps you are referring to the fact that refraction and other effects can cause deviations from values calculated for an ideal sphere, so that people may see something farther away than we predict mathematically, and claim that shows the earth is flat. Of course, gravity is not nearly enough to account for this (except, say, near the sun).
But your first comment is not really relevant. It’s not that the distance is measured in square miles, but that the apparent drop is proportional to the square of the distance, and many people are not familiar with such non-linear proportionality, leading to ideas such as we saw in the post, thinking the curvature is “8 inches per mile”. (Something similar arises in gravitation, where the force of gravity is inversely proportional to the square of the distance. There’s no area involved there, either.)
Hey I was looking for an explanation as to how much curvature is adjusted for when a sr-71 blackbird can fly 3659 miles in under two hours from New York to london.
I don’t know what curvature has to do with that. You’d have to ask the Air Force.
They would have to know the shape of the earth in order to navigate what I assume would be an approximate great circle route, but the amount of curvature would not be directly involved, as far as I can see, since they’d be flying at a set altitude over the curved earth, not in a straight line.
You seem to have added a couple hundred miles to the distance, compared to sources I find, which say it was 3461 (statute) miles. Are you assuming a longer route?
Today I could clearly see an unobscured Isle of Whyte even though it was 45 miles away and the sea looked perfectly flat
I am a retired chartered surveyor and I am now questioning whether the Earth is a sphere
I am very confused! I find no “Isle of Whyte” anywhere; if you are referring to the Isle of Wight in the UK, the map shows no location on land 45 miles away, from which you could have an unobstructed view of the island (which is only a couple miles from the mainland). Is this just a joke?
Please write to us through the Ask a Question link so we can discuss the details: where you are, what you see, and so on. You could even include a photo. (This sort of discussion is not appropriate in our comments.)
By the way, this particular question belongs on a different page, How Far Can I See?, where we find that if you were about 6 feet tall standing at the water’s edge, you could see the opposite water’s edge up to about 3 miles away. If you were a little higher up, you could see farther. (Standing on a road 10 feet above sea level, you might see about 5 miles.)
To resolve a discussion. If I were standing on a hill here in Ireland and assuming my eye level above sea level is approx 546 feet and looking across to Cumbria in England approx 85 miles away. What would the height of a land mass above sea level in Cumbria have to be in order that I could see it? Hoping you can resolve this difference of opinions. Many thanks. Noel
Hi, Noel.
Math can’t fully resolve such a discussion, because effects such as refraction will have an effect on what you can actually see. But the formula you need is found in the related page How Far Can I See?: \(s = \sqrt{2Rh}\), where R is the radius of the earth (about 4000 miles), h is the height above sea level (converted to miles), and s is the distance to the horizon. The total distance you can see is the sum of the distances to the horizon from the two ends.
From a height of 546 feet, the horizon would be about $$s = \sqrt{2\cdot4000\cdot\frac{546}{5280}}=28.8\text{ miles}$$. This leaves \(85-28.8=56.2\) miles for the Cumbrian horizon; solving for the height, $$h=\frac{s^2}{2R}=\frac{56.2^2}{2\cdot4000}=0.395\text{ mi}=2084\text{ ft}$$
Of course, that height probably is not located at the same distance you indicate, so some further adjustments would be needed, in addition to any practical considerations of viewing.
So, what was the discussion?
I was fascinated by this discussion and wanted some numbers, so I wrote a short Python program to calculate the obscured height by horizontal (arc) distance. I took a slightly different approach to the calculation and used the Cosine of the angle subtended at the centre of the earth, rather than Pythagoras, but the results should be the same.
It has no pretties or error checking, I leave that as an exercise for the reader, and I have calculated each stage separately to illustrate the method. Here it is in case anyone else wants to play with it.
#!/usr/bin/env python3
#
# File: curvature.py
# Author: R.D.Jones
# Created: 1st August 2024
#
# Copyright (c) 2024 R.D.Jones all rights reserved, unlimited use is granted for academic purposes only
#
# A Python program to calculate how much of a vertical structure is
# obscured by the curvature of the Earth at a specified distance.
#
# The program makes the following assumptions:
#
# – that the height of the viewpoint above ground is negligible
# compared to the radius of the earth.
#
# – that there is no significant difference in the heights of the
# viewpoint and the base of the structure. If the viewpoint is higher
# than the viewed structure, you can correct by using the program to
# find the distance at which the obscured height is the same as the
# height of the viewpoint, then subtract that distance from the
# distance to the viewed structure. A negative distance means that
# the structure is fully visible.
#
# e.g. for a six foot person standing on a shoreline looking at a
# floating object or a structure on a distant shoreline you should
# subtract about 4.8km from the specified distance.
#
# The results would be wildly inaccurate for, say, a viewpoint on an
# aircraft flying at 25,000 feet. Using the above method to calculate
# the correction shows that anything within almost 200 miles (~310km)
# would be fully visible, subject always to atmospheric effects..
#
# Returns: None
#
#———————————————————————–
from math import *
d = 6378 # approx radius of earth at MSL in kilometres
l = input(“What horizontal distance (in kilometres)? “)
theta = float(l) / d # angle subtended at centre of Earth (in radians)
dprime = d / cos(theta)
height = (dprime – d) * 1000
print (f”Cutoff height is {height:.3f} metres”)
Hi, Rob.
I don’t know why everyone writes about this sort of calculation as a comment on this post, when it is far more closely related to what we say in How Far Can I See? where we calculate distances to the horizon.
Your formula is correct; it can be derived from one in that page, namely $$s = r\cos^{-1}\frac{r}{r+h}$$ where r is the radius of the earth, h is the height above the surface, and s is the distance to the horizon. In your problem, you are finding the height on a distant building, from which you would be seen on the horizon.
Solving that for h, we get $$h=\frac{r}{\cos\left(\frac{s}{r}\right)}-r$$ That is essentially what your program does (with a conversion to meters).
Mostly because this page came up in a search about visibility of distant objects and it prompted me to respond.
I’ve always been fascinated by this since, over half a century ago, I lived for a while in Africa and could clearly see out of our living room window (at about 3,000 feet) a mountain range that rises to about 7,000 feet. The range was about 40 miles away and its base was at about 2,000 feet elevation (i.e. about 1,000 feet lower than our window).
My interest was further piqued on a flight back to the UK where the pilot casually mentioned that he could clearly see the weather over Mount Kenya about 200 miles away.
Also, running the program gave some results that really surprised me and I thought that students might find it fun to play with.
How accurate is this earth curve calculator (using imperial measurements) assuming one is standing on boat, calm day, calm lake, allow 6 feet eye height target distance 37.5 miles and maximum light refraction?:
https://dizzib.github.io/earth/curve-calc/?d0=50&h0=1667&unit=imperial
For both the default input it comes up with, and the example you ask about, it gives a number just a little more than I get using the formulas from the companion page How Far Can I See? (which doesn’t take refraction into account). I can’t say anything about how much refraction would affect it, as that depends on real-world considerations beyond the math. (The differences may be entirely due to my rounding rather than refraction.)