Last time we looked at a couple questions about proving the earth is round, which led into questions about how Eratosthenes measured the earth (though that in itself did not prove the earth is not flat). Let’s look at two questions about that project itself.
Eratosthenes for third graders
The first is from 1995, and comes from some students who probably aren’t ready for all the mathematical details:
Eratosthenes and the Circumference of the Earth Dear Dr. Math, How did Eratosthenes measure the circumference of the earth? Thanks, Our Third Grade Class
Doctor Andrew replied, with a little research:
Well, according to the Encyclopedia Americana and the Encyclopedia Britannica, Eratosthenes observed that at noon on the summer solstice (the longest day of the year) the sun was directly overhead in the city of Syene in Egypt (it is called Aswan now). I've heard elsewhere that he knew this because at that time, no shadow was cast in a well. A well isn't necessary to observe this though, since any container with parallel walls such as a box or a tube will not have a shadow when light comes from directly above it. Try it out yourself.
Here is an image from Encyclopaedia Britannica:
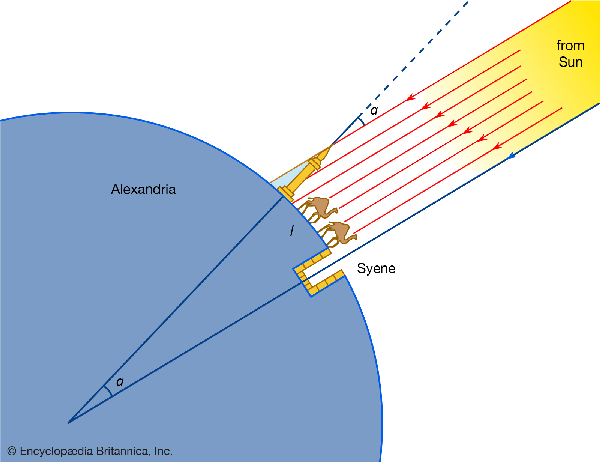
The important thing was that the sun hitting the entire bottom of a (vertical) well gave an accurate indication of a vertical beam of light. This situation will happen on the solstice anywhere on the Tropic of Cancer (the latitude line where the sun reaches farthest north, which was then in the constellation Cancer, the crab), 23.44° north of the Equator.
He then assumed that the sun was so far off that its rays hit the earth in parallel. If you imagine all the lines from the surface of one ball to another, you can see that as the balls get further apart, all the lines become nearly parallel. Parallel means that the lines all go in exactly the same direction. He also assumed that the earth was shaped like a ball.
I mentioned this last time: The calculation is based on the assumption of a spherical earth, rather than in itself proving the latter.
He also knew that Syene was on the same meridian as the city of Alexandria. The earth is a ball that spins around a line called its axis. A meridian, (also called a line of longitude) is a line on the surface of the earth from one end of this axis to the other. I'm not sure how he knew these two cities were on the same meridian; maybe he knew that the sun set at the same time when it was directly between the two cities. If you follow a meridian all the way around the earth you get a circle, like the equator. Finally, Eratosthenes knew that the distance between Alexandria and Syene was 5000 stadia, a Greek unit for measuring length. This was about 500 miles.
So we have here a list of assumptions and facts, all of which are only approximate. In fact, Syene is not exactly due south of Alexandria, nor is it exactly 5000 stadia south, and it was perhaps not exactly on the Tropic. (Neither longitude nor distances could yet be measured exactly, as we can now.) We don’t even know exactly how long a stadium (or stadion, the Latin or Greek singular form of the unit, also translated as “stade” today to avoid confusion!) was. For more details, see Wikipedia.
The important thing is that these were all close enough to being true, that he could make a reasonable approximation.
So, on the summer solstice, at noon, in Alexandria, Eratosthenes measured the angle of the sun's rays. You could do this by finding the angle at which a shape casts the least shadow. Suppose you had a globe that had a metal band around it that could rotate around the globe but could also be completely horizontal (globes usually have bands around them that are vertical). You may have one like this in your classroom. If you take the globe out and then rotate this band until its shadow is only a line, it will be parallel to (in the same direction as) the rays of the sun. Think about what fraction of a whole circle you had to rotate the band. Well, Eratosthenes probably had a device similar to this which he had to rotate 1/50 of a whole circle to get it to line up with the sun's rays.
This measures angle α in the picture above.
Using a little geometry (that is a little tough for 3rd grade) he then knew that 5000 stadia was 1/50 of the circumference of the earth. This means that he needed to use 50 of these lengths to surround the earth. So he multiplied 5000 by 50 to get 250,000 stadia. Then he added 2000 more to make up for what he thought were bad measurements. So he calculated the circumference of the earth to be 252,000 stadia. We know that the distance between Alexandria and Syene is about 500 miles, so using his fraction 1/50, we can get the circumference of the earth to be about 500 * 50 = 25000 miles, which is about right. Since historians aren't sure how long one stadia is, we haven't been able to figure out how close Eratosthenes was to the correct answer, but we do know that the way he tried to solve the problem was correct. In those days they couldn't easily make very accurate measurements of the distance between two places, so this could cause a lot of error.
Wikipedia suggests that the change to 252,000 may have been done so that the resulting number would be “round”, in the sense of being divisible by every whole number from 1 to 10, making fractions easy. Unfortunately, we don’t even have Eratosthenes’ own book, just a popularization of it from perhaps hundreds of years later, so we can’t be sure exactly what he did, or why.
I hope this is all clear, but there are probably some messy points. If you have any questions about this, please send them to us. If you want to know how Eratosthenes used Geometry to show that the 1/50 of a circle on the angle measuring device means that the distance between the two cities was 1/50 of the circumference of the earth, I'd be glad to try to explain it.
Some details for adults
Another question, in 1996, provided the opportunity to go into a little more detail about the geometry:
How Did Eratosthenes Measure the Circumference of the Earth? How did Eratosthenes measure the circumference of the earth? As I understand the process, he measured the lengths of shadows of sticks at different locations on the same day and time of the year, so he had two right triangles, but they weren't similar. So what do I do? - Ed and Roxann
They are missing the specific fact about Syene’s missing shadow, which makes the work easier. But it isn’t essential, as we’ll see.
Doctor Ethan replied (we hadn’t yet worked out how to include pictures in our answers):
This will be a little hard to explain without a picture but I will do my best. Eratosthenes made a few assumptions. One was that the earth was a sphere and the other was that the sun's rays were parallel. Neither assumption is true, but both were close enough. We will make the same assumptions If the earth were flat and the sun's rays were parallel, if you put two sticks straight up a half mile away from each other then their shadow would make the same angle. But if the earth were curved, then the angle made by the shadows would be different. This difference can be used to figure out the circumference of the earth.
Without mentioning Syene (and supposing details that are completely contrary to fact!), he illustrated the idea:
Let's try an example. Let's say you are Eratosthenes in Athens and you have a stick sticking straight into the ground, and at high noon the sun is straight overhead so it leaves no shadow. But your friend is in Rome which is (I'm guessing) 400 miles away, and there at the same time the sun makes a shadow at a 30 degree angle. That means that in 400 miles what appears to be straight up and down is 30 degrees different from what it does in Athens. This means that you have moved 30 degrees around the Sphere (Earth) in those 400 miles. Well, since there are 360 degrees in a circle and 30/360 = 1/12, then 400 must be 1/12th of the total circumference of the Earth. So the circumference of the Earth is 12 * 400 or 4800 miles. Now take note: these numbers are made up and do not reflect Eratosthenes' calculations or the actual circumference of the Earth.
Observe that in this version, several details would be impossible to determine back then: You couldn’t synchronize the two measurements (since they had neither portable clocks nor instantaneous communication); and it would be very hard to measure accurate distances across the Mediterranean. Since Athens is north of the Tropic of Cancer, the sun is never directly overhead there. Yet the mathematics is identical to the real story.
You can see, by comparison, why the data Eratosthenes actually used was better: The (approximately) north-south line was important as a substitute for synchronization, making noon essentially synchronous in the two places; and the distance over that route was relatively easy to measure. And the discovery that Syene was on the Tropic was a matter of good luck; anywhere between the two Tropics would have been usable, but it would be necessary to determine the appropriate date and time on which to measure.
Ed and Roxann responded,
Thanks, it's so easy now. I tend to get myopic when I start down the wrong path.
In fact, their original idea of measuring the shadows of two sticks would work, if synchronization were possible; so today you could just pick two locations far enough apart, and measure the shadows at the same moment. (I have heard of students doing just this.) What you would need to do then would be to use the shadows to calculate the angles of the sun, and work with the difference of those angles much as Eratosthenes did with the single angle at Alexandria. For example, if our two vertical sticks were 500 miles apart, in any direction, then we might find at some moment that one shadow makes an angle of 10.3° from the vertical while the other is 17.5°; the difference of 7.2° would lead to the same calculations we did above: 7.2° is 1/50 of 360°, so our 500 miles is 1/50 of the circumference of the earth, which is therefore \(50\times 500 = 25,000\text{ miles}\):
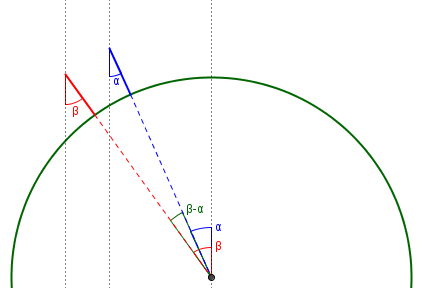
How much was luck?
Nine years later (2005), we got a challenge to the details given in the first answer above, which was added to this page:
I have just read your version of the Eratosthenes story about finding the circumference of the earth and have seen it twice before. If I understand the story appropriately Eratosthenes was in Syene or Aswan and knew when the sun cast effectively no shadow, but how could he figure out the angle of the shadow at that same moment in Alexandria, 500 miles away? Also, the 500 miles is close to the correct distance but not as the crow flies, or not exactly as the arc of the earth. The timing, distance and rough measurements all seem to add up to an inaccurate but ingenious approach. Could you explain how he was so accurate given the margin of error of all the calculations? My thoughts are the timing of the shadow needs to be fairly accurate because the sun is in constant motion so the angle would be constantly changing. The ground and route taken from Syene to Alexandria is not exact either, what if the route was measured by circumventing natural obstacles or by measuring both up and down a hill? He was apparently within 4 percent, but that seems more luck than anything, even given Fermi's reasonableness estimations.
Dr. Rick answered:
Hi, Greg. Here is one site that explains the situation in some historical detail: Measuring the Solar System (Michael Fowler, UVa) http://galileoandeinstein.physics.virginia.edu/lectures/gkastr1.html I can't answer all your questions, but I can at least put one to rest. There is no significant issue with the timing of the sightings. If the sun is directly overhead, it must be noon (well, what navigators call "local apparent noon") when the sun is highest. The sun can't be any higher than straight overhead. It was known that on a certain day (the summer solstice) the sun passed directly overhead at Syene. All that was necessary in regard to timing was to measure the elevation of the sun at its highest point on that day.
That is, we know the angle of elevation of the sun in Syene at noon, 90°; we just need to measure the angle at noon in Alexandria.
In celestial navigation, this is called a "noon sight" and is the easiest way to use a sextant to determine something about your position. Specifically, it tells you your latitude. All you need is a sextant and a table that gives the sun's elevation on each day of the year (or at closer intervals if you need more precision). You take a sight of the sun and continue adjusting the sextant until the sun starts going down. The highest value you found is the sun's elevation at local apparent noon.
So the measurement itself tells you the right moment: Noon is when the measurement you take is greatest.
The important thing about a noon sight is that you don't need a precise timepiece to do it. For other sights you do need to know exactly when you took the sight, because the sun moves east to west a lot faster than it moves north and south, due to the earth's rotation. This is the reason that old maps have much more accuracy in their latitudes than in their longitudes: accurate chronometers had not been developed. Dava Sobel's book "Longitude" tells the fascinating story of how this situation was remedied at last.
This, again, is why Doctor Ethan’s version of the story wouldn’t work back then: Getting the timing right for an east-west measurement would require a good clock, which is what solved the longitude problem.
Back to Eratosthenes, a factor that you didn't mention is the accuracy of the observation that Syene is due south of Alexandria. That's a second-order error, though (the error in the result varies as the square of the error in east-west position); I agree that the error in measuring the distance if the roads weren't straight is probably the major source of error. But I don't know how great his errors were, or even whether we can know. The site I linked above says that the length of Eratosthenes' unit of distance, the stade, is not known for sure, so we can't be sure how accurate his result was.
It is, indeed, considered partly a matter of luck that the measurement was so good; despite the ingenious method, the answer is closer than it deserves to be. Most likely modern tellings tend to choose the length of a stade, and other factors, so as to make the answer as good as possible (though the goal may also be to make the numbers and explanation simple). Wikipedia says that Eratosthenes “estimated that the meridian has a length of 252,000 stadia, with an error on the real value between −2.4% and +0.8% (assuming a value for the stadion between 155 and 160 metres).” Luck or not, that’s pretty good!

Pingback: How Much Does the Earth Curve? – The Math Doctors