We have been looking at questions about the roundness of the earth, starting with the general fact, and then the determination of the size of the earth. A very common question is about how that roundness affects what we can see, sometimes as a challenge (“If I can see this, then how can the earth be round?”), and much more often out of curiosity (“How far can I see if …?). We’ll look at a few of the latter questions here.
Finding the horizon
This question, not the first of its type, is from 1999:
Distance to the Horizon How far is the horizon?
That needs clarification! Doctor FWG offered a specific setting:
Dear Robert, Thanks for sending this interesting question. However, it is difficult to answer exactly because certain conditions must be specified, whether they happen to exist or not. For example, one estimate of the distance to "the" horizon can be made if one assumes a perfectly smooth surface for the earth and an observer looking toward the horizon with his/her eye level exactly 5.28 ft (or "h") above the earth's surface (this height is arbitrary but the value used for it will affect the final answer). The nearest approximation of this condition might exist for a short person standing in a row boat floating in the middle of a very large (calm) lake.
Since the height of the eye above the surface will vary, and the radius of the earth has to be looked up (and will vary depending on how a source interprets it, since the earth is not an exact sphere), it is best to use variables for them. And since we are making a number of assumptions, any answer we give will be approximate.
The assumed eye height of 5.28 feet chosen for a reason we’ll see soon, but is not unreasonable. Because the earth is not an exact sphere, its radius varies; it is 3963 miles at the equator. The mean radius is calculated as 3,958.7613 miles, but at any particular location and direction it can vary from about 3,936 to 3,977 miles (6335 to 6400 km). We’ll be approximating it by a round 4000 miles here.
If you now assume that the distance from the center of the earth to the earth's "perfectly spherical" surface is exactly 4,000 mi (or "R") and that the distance from the center of the earth to the short person's eye level is 4,000 mi plus 5.28 ft (or R + h), you can estimate the distance to the horizon (assuming no other problems, such as refraction or bending of light coming from the horizon to the observer's eyes). Let "s" stand for the actual distance between the observer's eyes and the horizon. You also need to assume that rays of light coming from the horizon to the observer's eyes make a right angle with the earth's radius vector at the horizon. In other words, the light rays coming from the horizon point to the observer's eyes are tangent to the earth's "surface" at the horizon point. You may ignore the actual curvature of the earth and assume that "s" and the actual distance between the observer and the horizon, along the curved part of the earth's surface, are equivalent. From these conditions and approximations, you can draw a "right" triangle and then use the Theorem of Pythagoras to estimate the distance to the apparent horizon.
Here is a picture to illustrate (highly exaggerated so we can see it):
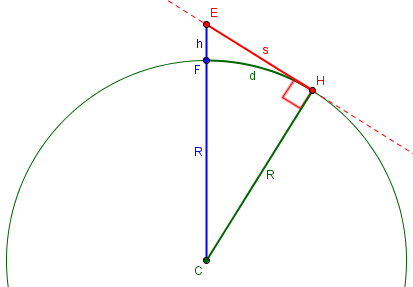
Here, C is the center of the earth, E is your eye, F is your foot, and H is a point on the horizon; s is the straight-line distance to the horizon, d is the walking distance to the horizon, h is your height, and R is the radius of the earth. In the picture h is not very small compared to R; this is a very tall tower! If h were much smaller, you can see that s and d would be essentially the same. We’ll be using that fact.
Using the Theorem of Pythagoras and the conditions above, you can write:
R^2 + s^2 = (R+h)^2 = R^2 + 2Rh + h^2,
or
s^2 = 2Rh + h^2 = h(2R + h).
But 2R is much greater than h, so:
s^2 = h(2R), approximately,
or
s^2 = 2Rh.
This gave us an exact formula, $$s = \sqrt{h(2R + h)},$$ and an approximate but simpler formula, $$s = \sqrt{2Rh}$$ that is applicable as long as our height is significantly less than the earth’s diameter.
Now we can apply this to the assumed measurements, being careful to convert everything to the same unit, in this case miles:
Therefore: s = Sqrt(2Rh) = Sqrt[2(4000 mi)(5.28 ft/5280 ft/mi)] = Sqrt[(8000)(0.001)] = Sqrt[8] = Sqrt[(4)(2)] = 2[Sqrt(2)] = 2(1.414) = 2.8 mi. So, for these conditions, the distance to the horizon is about 2.8 mi. I hope this has been helpful.
You can see now where that assumed height of 5.28 feet came from! It was chosen to produce simple numbers after conversion to miles.
What if we’d used the exact formula? $$s = \sqrt{h(2R + h)} = \sqrt{\frac{5.28}{5280}\left(2(4000) + \frac{5.28}{5280}\right)} = \sqrt{0.001(2(4000) + 0.001)} = \sqrt{8.000001} \approx 2.828\text{ miles}$$ As you can see, it made no difference. This is why the approximation is entirely reasonable.
What if we stood at the top of a cliff, so that our eyes were 100 feet above the water? $$s = \sqrt{2Rh} = \sqrt{2(4000)\left(\frac{100}{5280}\right)} = 12.3\text{ miles}$$
Beyond the horizon
The next question is from 2005, and deals not with the horizon (seeing an object right on the surface), but a tall object beyond the horizon. That is, the first question deals with seeing the waterline of a boat, while this one could be the top of a mast.
Line of Sight Distances between Two Objects An offshore drilling rig is being towed out to sea. What is the maximum distance that the navigation lights can still be seen by an observer standing at the shoreline? The observer's eye height is 5'9", and the uppermost navigation light is 225 feet above the water. Give your answer in miles. I'm confused because I believe there is a lack of direct information to find out the exact answer, like the curvature of earth. That should play a role, but that's what I'm unsure of. How does it play a role, and is there a formula to determine when a line of sight will be lost? I know that the radius of the earth is 3959 miles.
Because the light is above the water level, we will be able to see it past the horizon. In fact, the farthest we can see will just graze the horizon, tangent to the earth. So we can use the same thinking here:
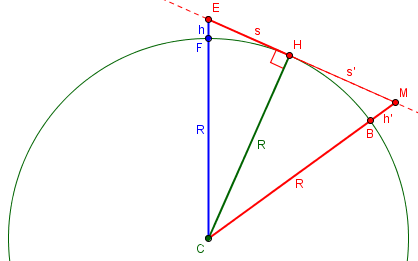
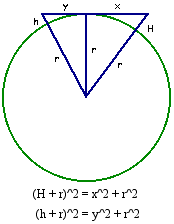
Doctor Jerry responded:
Hi Kenneth-- Thanks for writing to Dr. Math. Imagine a sector of a circle with represents the Earth (like a slice of pie). At one end of the sector's arc erect a tower of height H and at the other end erect a tower of height h. The tops of these are the points between which we want to decide upon the longest line-of-sight distance. Draw a line connecting the tops. We want to adjust the size of the sector so that this sight line is tangent to the circle at a point between the two bases. If the two towers were further apart, they could not see each other.
Imagine a straight wire stretched from our eye at height h and the light at height H, and moving H farther away until the wire just touches the earth at our horizon; that is the farthest it can go.
Now draw a radius from the center of the Earth to the point of tangency between the sight line and the circle, and recall that the radius and the tangent line will be perpendicular. Thus, we have two right triangles, one on either side of the radius to the tangent point. One of these triangles has hypotenuse H + r and the other h + r. So we see that (H + r)^2 = x^2 + r^2 (h + r)^2 = y^2 + r^2 You can see this all set up here:
In effect, we are finding x, the distance from the eye to our horizon, and y, the distance from the light to its horizon, and adding them to find the total distance.
The maximum line-of-sight distance is x + y. Solving the first equation above for x:
x^2 + r^2 = (H + r)^2
x^2 + r^2 = H^2 + 2Hr + r^2
x^2 = H^2 + 2Hr
x = SQRT(H^2 + 2Hr)
Following the same steps to solve the second equation for y, we can then express x + y as:
x + y = SQRT(H^2 + 2Hr) + SQRT(h^2 + 2hr)
Using the values of r, h, and H you gave before, I find the maximum line of sight between the rig and the person to be x + y = 21.3 miles.
This formula will work for any line of sight problem between two objects of known heights (H and h) above the Earth.
We are adding two copies of our exact formula from before, $$D = \sqrt{H^2 + 2Hr} + \sqrt{h^2 + 2hr}.$$ We could also use the approximate form, as long as the heights are not too great (measured in feet rather than miles, say): $$D \approx \sqrt{2Hr} + \sqrt{2hr}.$$ Using the latter for the example, we get the same result: $$h = {5}’ {9}” = 5.75\text{ ft} = \frac{5.75}{5280}\text{ mi} = 0.001089\text{ mi}\\H = 225\text{ ft} = \frac{225}{5280}\text{ mi} = 0.04261\text{ mi}\\D \approx \sqrt{2(0.04261)(3959)} + \sqrt{2(0.001089)(3959)} = 18.4 +2.9 = 21.3\text{ mi}.$$ We can see that our horizon is 2.9 miles, while that of the light is 18.4 miles.
Off-the-wall tall, with trig
Let’s look at one more question, similar to that last one, from 2001:
The Top of the Tower Given a 300-mile-tall tower on the earth, how far away from it can you go before the top disappears below the horizon? (Assume unlimited visibility.) We've drawn diagrams and triangles to try to figure it out using trigonometry, but we're looking for an equation(s) that will help us get the answer.
This time we won’t be able to use a small-height approximation, will we?
From the ground
Doctor Ian answered, starting with a simple case where you are on the tower’s horizon:
Hi Ashley,
It's hard to draw a circle with a keyboard, but let's pretend this is the earth:
.
. .
. .
. .
. .
. .
.
Also, let's pretend the earth is a sphere, and that it's perfectly smooth, even though neither of those things is true.
If your eye is at ground level at some point, then you can look out tangent to the earth:
<------------------
. .
. .
. .
. .
. .
.
If the top of a tower of height h just intersects your line of sight,
<-----------.------
. . .
. . h
. .
. .
. .
.
then you can form a right triangle with you, the center of the earth, and the tip of the tower at the corners:
A C
<-----------.------
. . . .
. . . h
. .
. . .
B
. .
. .
.
This is the same triangle we used to find the distance to the horizon. But he’s going to use trigonometry rather than just the Pythagorean theorem, and for a good reason: With such a tall tower, line-of-sight distance is not the same as walking distance!
If the radius of the earth (in miles) is r, then
AB = r
BC = r + h
and
r
cos(ABC) = -----
r + h
This is the ratio of “adjacent leg” to “hypotenuse”.
On a sphere, the distance along the surface (s) corresponding to a central angle theta is
s = r * theta
So the distance you'd have to walk from point A to the base of the tower would be
s = r * theta
r
= r * arccos( ----- )
r + h
For r = 3950 miles and h = 300 miles,
3950
s = 3950 * arccos( ---- )
4250
= 1493 miles
Our formula this time is $$s = r\cos^{-1}\frac{r}{r+h}$$ The line-of-sight distance from our first answer would be $$s = \sqrt{h(2R + h)} = \sqrt{300(2(3950) + 300)} = 1568\text{ mi},$$ which is considerably longer.
A reality check: the Sears Tower
That seems like a pretty long distance! Is it reasonable? It's tough to visualize something 300 miles tall. Let's think about something more realistic, like the Sears Tower.
The Sears tower is 1450 feet tall, which works out to be about 0.275 miles. So our equation says that we should be able to see it up to
3950
s = 3950 * arccos( -------- )
3950.275
= 46.6 miles
which means that you would just be able to see the Sears tower from the Indiana Dunes State park - if you were lying on the ground. I know for a fact that you can see it from there standing up, because I grew up near there.
This refers, of course, to seeing the top of the tower.
Many of the questions we get arguing for a flat earth are based on personal experience or photos of buildings from a great distance. Sometimes their observations appear to depend on a bad memory or atmospheric bending of light, but the main answer for such people is that if the earth were flat, you should be able to see the base of any building from any distance away …
From above the ground
That was the easy case. How much changes if you stand up (or go to the top of a cliff or a building, or whatever)? We know what to do already, don’t we?
Okay, so what if you're _not_ lying on the ground?
Well, think about this problem. If your eye is height h' above the ground, what's the farthest point you can see?
A'
| h'
| .
. . .
. . . C'
. .
. . .
B
. .
. .
.
Now we have a different right triangle (A'C'B is the right angle), and we know that
r
cos(A'BC') = ------
r + h'
This looks familiar, doesn't it?
This is, of course, the same formula in reverse: the trig version of our horizon formula.
Now extend the line A'C', and you have the same problem we just solved. The central angle is now (A'BC' + ABC), so
s = r * (A'BC' + ABC)
r r
= r *[arcos( ------ ) + arccos( ----- )]
r + h' r + h
As before, we just add two copies of the horizon formula: $$s = r\cos^{-1}\frac{r}{r+h’} + r\cos^{-1}\frac{r}{r+h}$$
More reality
Let's check that again for the Sears Tower. If you're 6 feet tall, that's about 0.0011 miles tall, so
3950 3950
s = 3950 * [arccos( --------- ) + arccos( -------- )]
3950.0011 3950.275
= 49.6 miles
which isn't a lot of difference.
Standing up added about 3 miles – the distance to our horizon.
Now, here's the interesting thing. From Indiana, it seems as though you can see, not just the top of the building, but the top half. The greatest distance from which that should be possible is
3950 3950
s = 3950 * [arccos( --------- ) + arccos( --------- )]
3950.0011 3950.1375
= 35.9 miles
I just checked with maps.yahoo.com, and the driving distance from the house where I grew up in Indiana (just outside the Dunes State Park) to the Sears Tower is 49.7 miles, and the distance from the Dunes State Park to the Sears Tower is a little less than 40 miles (as measured on the map that accompanies the driving instructions). So this appears to work out quite well.
It’s nice when math matches memory.