(A new question of the week)
Last week we looked at a question about a triangle inscribed in a semicircle. Not long after that question, the same student, Kurisada, asked a question about triangle inscribed in a circle, which had some connections to the other. As we enjoy doing, we led the student through several possible approaches to a solution. It also illustrates a situation where different methods can lead to what appear to be entirely different answers, yet they may be identical.
Finding the sides of a triangle in a circle
Here is the new problem, from the very end of last December:
A circle O is circumscribed around a triangle ABC, and its radius is r. The angles of the triangle are CAB = a, ABC = b, BCA = c. When a = 75°, b = 60°, c = 45° and r = 1, the length of sides AB, BC, and CA are calculated as ____, ____, ____ without using trigonometric functions.
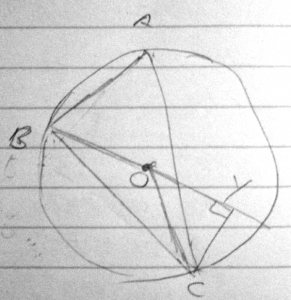
Here is a picture showing all the information we have:
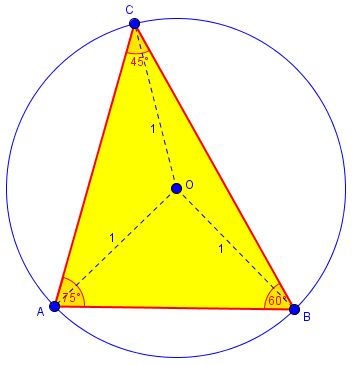
Using trigonometry, we could find the sides if we knew one of them; but the only length we have is the circumradius (the radius of the circumscribed circle). With no formula for this radius, and no trigonometry, how are we to do this?
Since all we were given was the problem, Doctor Rick responded with just a hint, and the usual request to see work:
Hi, Kurisada. This is another interesting problem!
As a start, I suggest constructing the radii OA, OB, and OC, and determining the interior angles of the triangles AOB, BOC, and COA. I can think of several ways to do this.
Many of the angles you will now find in these three triangles will be familiar angles that you know how to work with. The most challenging may bring to mind one of the problems we have discussed with you before. See what you can do now.
Drawing in the radii, as I already did above, is a standard first step, as they must be involved in the solution. Doctor Rick’s work, as suggested, involved a triangle similar to one from last week’s problem, but that is not the only way.
Kurisada replied:
I found that AOB is 90° and thus, AB is √2.
I’ve also found another angle but I wasn’t able to find AC and BC without using trigonometry ratio.
Triangle AOC has the angles 120°, 30°, and 30°.
And triangle BOC has the angles 150°, 15°, and 15°.
Did I miss something?
Here is what we have now:
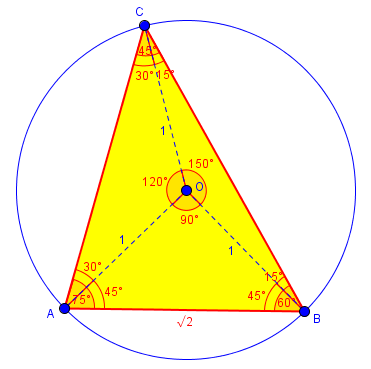
As Doctor Rick said, there are several ways to have found these angles; one is to use the fact that a central angle is twice the inscribed angle, so that for instance ∠AOB = 2∠ACB = 90°. Since the triangle is isosceles, the other angles are both 45°.
Doctor Rick replied, having only started work on actually solving the problem himself, but adding more hints on the harder two triangles:
You’ve done well so far. You’ve got the easiest side, AB.
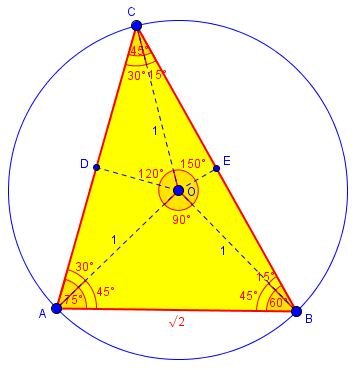
For side AC, consider that triangle AOC is isosceles, and construct the altitude to AC.
Side BC is the most challenging part that I mentioned. Notice that when you construct the altitude to BC, you’ll have the same right triangle that turned out to be the answer in the triangle-in-a-semicircle problem: 15-75-90. Applying things we learned there can help us find the area of triangle BOC pretty easily, but I’m not sure how much that helps. Let’s both work on this!
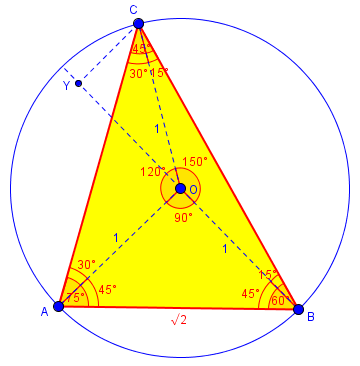
Here is the figure with those two altitudes added; the first yields 30-60-90 triangles, which are easily solved, and the second gives the triangles we saw in the other problem:
I had another idea, and jumped in briefly:
Here is an alternative: Having found AB, construct the altitude from A to BC. Several things work out nicely.
Doctor Rick by now had finished his work, and added:
I found a fairly simple way to complete the work I started … it involves extending BO to the other side of the circle and constructing the perpendicular from C to this line.
Then, recall our work on the triangle in a semicircle, and construct the radius OC as well, which makes another 30-60-90 triangle.
However, my solution has nested square roots, whereas Doctor Peterson’s solution has a sum of square roots. It can be shown that the two solutions are equal, but his is “nicer” — we don’t really like nested roots.
From here on, the actual interaction mingled work on the two approaches in a way that is very hard to follow, so I am going to break with tradition and untangle these into two separate threads. (It was not easy, especially because there were also several typos and consequent confusion to edit out.) First, we’ll follow the discussion of Doctor Rick’s idea.
Method 1
Kurisada now showed his work:
Focusing on the doctor’s statement about 30-60-90, then I thought that there is a fixed ratio of the sides of 30-60-90 triangle.
I searched it and I found the ratio 1 : √3 : 2.
I wrote the perpendicular point from C to line BO after extended as Y (sorry for my bad English in this, but I attached the picture below).
And I take the triangle COY with angles 30-60-90.
Since OC = 1, then OY = (√3)/2, and CY = 1/2.
Then I take triangle BCY.
CY = 1/2 and BY = 1 + (√3)/2.
Then using Pythagoras Theorem, I got BC = √(2 + √3).
The key answer shows that BC = (√6 + √2)/2.
I wonder if I did anything wrong.
I also wonder if what doctor wanted to tell me is as above or not.
I also tried to apply about my previous problem (triangle inside a semicircle), but I can’t find something to apply to this problem especially the non-trigonometry one. Can doctor give me a little more clue?
Nothing is wrong. Kurisada has done well, and as mentioned earlier, the answers are equivalent.
Doctor Rick replied (using a picture I’ve replaced with one of my own to correct an error):
Here is my figure for this solution method:
There are several ways to prove that angle COY is 30°.
“Focusing on the doctor’s statement about 30-60-90, then I thought that there is a fixed ratio of the sides of 30-60-90 triangle
I searched it and I found the ratio 1 : √3 : 2″
I had assumed you were already familiar with this fact, as we used it in discussing the previous problem with you. It is easily derived by starting with an equilateral triangle and constructing an altitude (which is also a perpendicular bisector and an angle bisector). This forms two 30-60-90 triangles. The side opposite the 30° angle is half of a side of the equilateral triangle, and hence half of the hypotenuse of the 30-60-90 triangle. The length of the remaining side follows via the Pythagorean Theorem.
“And I take the triangle COY with angles 30-60-90.
Since OC = 1, then OY = (√3)/2, and CY = 1/2.
Then I take triangle BCY.
CY = 1/2 and BY = 1 + (√3)/2.
Then using Pythagoras Theorem, I got BC = √(2 + √3).
The key answer shows that BC = (√6 + √2)/2.
I wonder if I did anything wrong.”
No, you haven’t done anything wrong. As I said last time, this method results in an answer with a nested square root — exactly what you found, √(2 + √3) — while Doctor Peterson’s method gives a sum of roots — as your answer key does, (√6 + √2)/2. And I said that these can be proved to be equal, but this is far from obvious at first! I suppose, therefore, that the answer in the key was obtained by something more like Doctor Peterson’s method.
“I also wonder if what doctor wanted to tell me is as above or not.”
You did fine using this method. If you finish the work by Doctor Peterson’s method, you should obtain the book’s answer.
We’ll get to the direct route to the answer \(\frac{\sqrt{6}+\sqrt{2}}{2}\); but in order to see that the two answers are equal, that is, that $$\sqrt{2 + \sqrt{3}} = \frac{\sqrt{6}+\sqrt{2}}{2},$$ we can just square both sides (having observed that both sides are positive, so that squaring does not lose information): On the left, $$\left(\sqrt{2 + \sqrt{3}}\right)^2 = 2 + \sqrt{3},$$ while on the right, $$\left(\frac{\sqrt{6}+\sqrt{2}}{2}\right)^2 = \frac{6 + 2\sqrt{6}\sqrt{2} + 2}{4} = \frac{8 + 2\sqrt{12}}{4} = 2 + \sqrt{3}.$$ So the two sides are in fact equal.
Continuing,
“I also tried to apply about my previous problem (triangle inside a semicircle), but I can’t find something to apply to this problem especially the non-trigonometry one. Can doctor give me a little more clue?”
In my non-trig solution to that other problem, I constructed the radius equivalent to OC in this problem. If, in figure (b), we give the name F to the other intersection of BO extended with the circle, and construct FC, then triangle FCB is just the triangle inscribed in the semicircle of the other problem. It is a 15-75-90 triangle; its altitude OE is half the radius of the circle, as we discussed in that problem (as this makes the area of FCB half the maximal area of an inscribed triangle). Thus this new problem is nearly the reverse of the previous problem: there we needed to determine the angle FBC knowing the base and altitude of the triangle, whereas now we know the angles and need to determine the side lengths.
So Doctor Rick’s method gives a correct answer, and ties into what we looked at last week.
Method 2
Now let’s look at the discussion of my method, which was interlaced with that. Kurisada said:
I drew the altitude AD, and found that AD = DC since ADC is 90°, 45°, 45°.
But, I also did : BD x CD = AD^2, resulting BD = AD which I think is impossible as the angles are 90°, 60°, 30°.
I also tried to do AC ÷ AB = DC ÷ AD, but it resulted AC = AB which I think is also impossible due to the same reason as above.
Rick replied:
“I drew the altitude AD, and found that AD = DC since ADC is 90°, 45°, 45°.”
Correct.
“But, I also did : BD x CD = AD^2, resulting BD = AD which I think is impossible as the angles are 90°, 60°, 30°.”
The geometric mean property we discussed earlier [in the semicircle problem] applies only to a right triangle; ABC is not a right triangle. Or am I misunderstanding what you did here? The angles you cite are for triangle ADC.
But that, in fact, is exactly what Doctor Peterson was getting at (in part) — you can use the side ratios for a 30-60-90 triangle to determine your OC, and the side ratios of a 45-45-90 triangle to determine your OB. (This is after you’ve determined AC and AB as you indicated earlier.)
“I also tried to do AC ÷ AB = DC ÷ AD, but it resulted AC = AB which I think is also impossible due to the same reason as above.”
Presumably you are still talking about the theorem about a right triangle, in which there are three similar right triangles. That doesn’t apply here.
Kurisada answered:
I didn’t realise about the fact that the geometric mean is only applicable to right angle so what I did is wrong.
Rick answered (again, I had to replace his picture with one that is labeled correctly):
Doctor Peterson gave you a link to Wikipedia which calls the theorem the “right triangle altitude theorem or geometric mean theorem”. It’s important to be aware of the givens when you seek to apply a theorem!
Here is the figure for this solution:
Here, D is the foot of the perpendicular from A to BC, as Doctor Peterson had in mind. It should be obvious that triangle ABD is a 45-45-90 (right isosceles) triangle, since angle ABD = ABC is given as 45° and ADB is a right angle; and also obvious that triangle ACD is a 30-60-90 triangle since angle ACB = ACD is given as 60°. Now, early on, we discussed finding the lengths of AB and AC, so you should know those — do you? You said AB = √2, which is correct; perhaps you never finished finding AC.
Here’s what I said in my second message about that: “For side AC, consider that triangle AOC is isosceles, and construct the altitude to AC.” What do you find? I hope you’ll recognize two more of those 30-60-90 triangles that I had assumed you already understood.
Then CD = AC/√2, and BD = AB/2, by the side ratios for the two “special triangles”. Add these and you’ll get the length of BC, which is what we’re looking for.
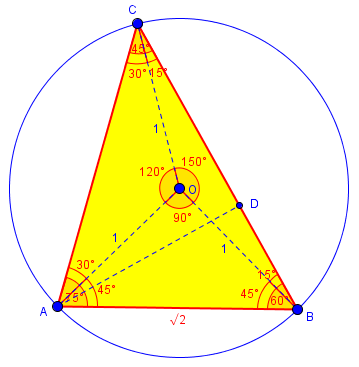
Let’s finish the work. Here is a picture with that altitude to AC, OE:
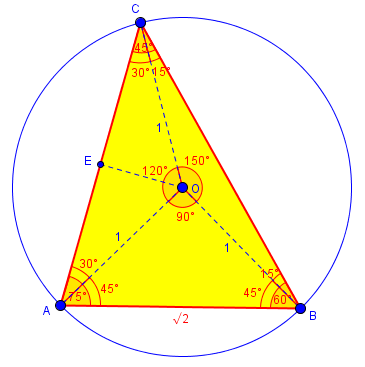
From triangle CEO, we see that \(CE = \frac{\sqrt{3}}{2}\), so $$AC = \sqrt{3}.$$ Then, going back to the previous picture, from triangles CAD and BAD we have \(CD = \frac{\sqrt{3}}{\sqrt{2}} = \frac{\sqrt{6}}{2}\), and \(BD = \frac{AD}{2} = \frac{\sqrt{2}}{2}\), so $$BC = BD + CD = \frac{\sqrt{6}+\sqrt{2}}{2}$$ as before. Those are our final answers.
Now Kurisada was satisfied:
Thank You very much Doctor Rick!
Now I understand about this problem
And sorry because it took too long time
The discussion concluded on January 1.
We do not mind taking time over a problem; we like going deeper to make sure a student understands the concepts fully. Thanks for sticking with this, and have a happy New Year!
…