Finding the Length of a Rolled-up Carpet

One of the more frequent questions we had on Ask Dr. Math was about how to find the length of material (carpet, paper, wire, etc.) on a roll, knowing only the inner and outer diameters and something else: the thickness of the material, or the number of turns, or the original size of the roll. Here we’ll look at several derivations of a formula, and variations of it.

Approximating a spiral

We’ll start with this reverse question from 1995, to establish the concept:

Calculating the Diameter of a Carpet Roll

How do you calculate the diameter of a carpet roll when you have the length and the thickness?

Doctor Andrew answered with some useful ideas:

Hi!  Great question.  For a darn good approximation you could find the cross-sectional area (the area of the circular end of the roll) needed for the roll, assume that the roll is a perfect cylinder, and then calculate the diameter required for that cross-sectional area.  If a carpet has length L and thickness t, the cross-sectional area of the roll is the same as the cross-sectional area of the edge of the carpet when it is lying on the floor, which is the very long rectangle with length L and thickness t.  See if you can take it from here to find the diameter.

Here are the dimensions he has in mind for such a perfect cylinder:

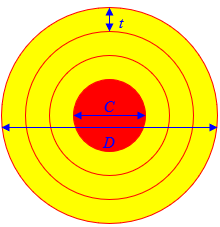
It has two diameters (the core, C, and the outer diameter, D), thickness t, and a length when rolled out, L:

(Not to scale!)

Neither of us has ever seen a carpet roll shaped perfectly cylindrically since it is a spiral with an edge that usually sticks out off the rest of the roll.  I imagine that trying to describe the shape of the spiral could be pretty tough.  You could probably come up with a number of approximations, the most accurate of which would take into account how the spiral begins and what kind of space would be left in the center of the roll due to physical limitations on how the carpet can bend.  You might notice that the approximation in the above paragraph becomes less and less accurate as the ratio of L to t (the fraction L/t) becomes smaller and smaller.  If you think more about it, you'll realize that when a carpet bends it is already changing its shape (stretching on the outside, compressing on the inside) in a way that makes describing it exactly with mathematics very difficult.

Here is a slightly better image of what the roll might look like, though the bend would not really be this smooth:

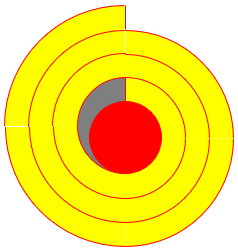
The more layers (and the thinner the carper), the closer we can approximate it with a cylinder.

In what follows, we’ll find the length given the dimensions of the roll, reversing what was said here. Most of the answers will be based on the area idea. Next time we’ll consider the compression issue.

Derivation from cross-section area

Next, from 1996, we get an actual formula:

Length of Material on a Cylindrical Roll

Is there a formula for calculating the length of material on a roll knowing the roll diameter, the core diameter, and the material thickness?

I recently tried using a formula I saw in a newsletter, but it was not even close when I tried a real life example.

The formula was something like (64.54*(D*D)-(C*C))/T*1000 where D is the roll diameter, C is the core diameter, and T is the thickness, all in inches.  The answer was supposedly in feet.

His formula, which is not quite written right, can be written correctly as $$\frac{64.54(D^2-C^2)}{1000T}$$

Doctor Anthony derived that formula, using the area approach and then converting to inches by dividing by 12:

The area of cross-section of the roll can be expressed in two ways.  When stretched out in a straight line it is a rectangle of area L*T where L is the length in inches, and T the thickness viewed edge on.  When rolled on the drum, this same cross-section will be pi*R^2 - pi*r^2 where R = outer radius (=D/2), and r = inner radius (=C/2)

So we have L*T = pi{D^2/4 - C^2/4}

             L = pi/(4T){D^2 - C^2}  inches

        Length = pi/(48T){D^2 - C^2} feet 

               = (0.06545/T){D^2 - C^2) feet  (T,D and C in inches)

Try this in real life.  It will be sensitive to the value of T you use, so measure that carefully.

That’s exactly the formula the anonymous questioner had seen. Without the unit conversion (so that the length is in whatever units you use for the other measurements), the formula is $$L=\frac{\pi(D^2-C^2)}{4T}$$

The last few answers here will look at substitutes for the thickness, making it easier to be accurate.

Derivation by summing the layers

For an alternative derivation of the same formula, consider this 2001 question:

Fabric Left on a Roll

I am going to write a program for my TI-83+ (I can also use a TI89 if necessary) to calculate how many feet of material are left on a roll.  I know the outside diameter of the core (this is the tube around which the film is wrapped, I know the outside diameter of the roll, and I know the thickness (mil thickness) of the material. What I don't know is the formula to use to calculate the feet of material left on the roll.

What I thought I could do is start out with the distance around the core. In this particular case, that would be pi*3.75 (the outside diameter). Then each additional layer of material would be the previous outside diameter plus twice the thickness (1 mil = 0.001").  I'd have a field in which I'd keep a running total of these inches.  I'd set up another field to keep track of the total number of "wraps" of material, which would be a calculated field (outside diameter of the roll/2 - 3.75/2 [this removes the core's dimension] divided by the mil thickness of the film). I'd put a loop in the program to keep adding to the running total of inches until the number of wraps = 0.

This would seem to be the hard way, but as I said, I don't know what formula to use. I know there has to be a formula I can use for this calculation to make things a lot easier. Does anybody out there know the formula I'm looking for?

Doctor Robert answered, using the suggested method and finding the same formula we’ve seen:

I'll take a whack at this one. No guarantee of success.

Let me define the diameter of the tube as Do and the diameter of the roll as D. Let t be the thickness of the material. Then I figure that the number of wraps, n, on the tube, is:

   n = (D-Do)/(2*t)

and we need to find the total length of these n wraps. 

I'll figure the length of a wrap to be the circumference of a circle whose radius is from the center of the tube to the center of the wrap I'm dealing with. In other words, the radius of the first wrap is Do/2 + (1/2)t; the radius of the second wrap is Do/2 + (3/2)t; the radius of the third wrap is Do/2 + (5/2)t.

Each layer add t to the radius, and thus \(2t\) to the diameter, so we divide the difference in diameters by \(2t\) to count the layers.

He is using the radius to the middle of each layer (figuring that each layer is compressed on the inside and stretched on the outside), so he takes the first layer as having radius \(\frac{t}{2}\) more than the core radius, and adds t to the radius for each layer. This makes an arithmetic series:

Now the circumference is 2pi times the radius and we need to sum a bunch of circumferences. Generalizing on the formula above, the radius of the kth wrap is:     

   radius of kth wrap = Do/2 + t(2k-1)/2  where k= 1,2,3,...

   Length of material 

     = sum from k=1 to n of 2*pi*[Do/2 + t*(2k-1)/2]

     = n*2*pi*Do/2 + sum from k=1 to n of 2*pi*t(2k-1)/2)

     = n*pi*Do + pi*t times sum from k=1 to n of (2k-1)

Now the sum of 1+3+5 + ...+2n-1 = n^2

So,  length = n*pi*Do + pi*t*n^2

But   length = n*pi(Do + n*t)

But n = (D-Do)/(2t)  so the formula is

      Length = (D-Do)*pi/(2t)*[Do + (D-Do)/2]

             = (D-Do)*pi/(4t)[Do+D]

             = (D^2-Do^2)*pi/(4t)

I hope that this formula is correct and serves you well.  There is no guarantee.

The summation is $$\sum_{k=1}^n 2\pi\left[\frac{D_o}{2}+\frac{t(2k-1)}{2}\right]=n\pi D_o+\pi t\sum_{k=1}^n (2k-1)\\=n\pi D_o+\pi tn^2=\pi n(D_o+nt)$$ This uses the fact that the sum of n consecutive odd numbers is \(n^2\), which we proved in Inductive Proofs: Four Examples.

So the formula becomes $$L=\pi\cdot\frac{(D-D_o)}{2t}\cdot\left[D_o+\frac{D-D_o}{2}\right]\\=\frac{\pi(D-D_o)}{2t}\cdot\frac{D+D_o}{2}=\frac{\pi(D^2-D_o^2)}{4t}$$

Note that this gives the same formula as before, by adding all the layers in our idealized cylinder.

Derivation from average length of a layer

This question from 2003 provides a slightly different approach equivalent to the same idea:

Determining Length of Material Remaining on a Roll

Many apologies if this is not what you do, but I'm at a loss for where to find this answer.

I need to know the mathematical formula to determine the length of material as it is on a roll.  Specifically; my company supplies rubber and tape, both in rolls on a core.   Without unrolling the roll, we'd like to determine the length of the material with the following information:   Outside diameter of the core, outside diameter of the whole roll and thickness of the material (determined by a micrometer).   

Do you have any such formula?

We do, indeed!

I answered, starting with links to the answers above and below:

Hi, Laura.

We get this question a lot; here are some of the explanations in our archive:

  Length of Material on a Cylindrical Roll
    http://mathforum.org/library/drmath/view/51723.html 

  How Much Carpet is Left?
    http://mathforum.org/library/drmath/view/56481.html 

  Fabric Left on a Roll
    http://mathforum.org/library/drmath/view/54357.html 

Briefly, the length of the material will be the product of the number of layers and the average length of one layer in the roll. Both are easy to find: Number of layers = (Do-Di)/(2t) [total thickness/one layer] Average layer = pi(Do+Di)/2 [circumference at average diameter] where Do and Di are the outer and inner diameters, and t is the thickness of the material. So the length is L = pi(Do+Di)(Do-Di)/(4t) = pi/4 (Do^2 - Di^2)/t

We get the same formula; the idea is that the sum of an arithmetic series is the number of terms times the average of all the terms, which is the average of the first and last.

A small error in the thickness measurement can make a big difference; I would recommend measuring it not with a micrometer, but by measuring the outside diameter of a roll of known length and calculating t from this formula in reverse. That will ensure that the number you use reflects the way the material lies on the roll. But try both measurements to see how they compare.

This last comment has great practical importance. Not only is it hard to accurately measure a small thickness, but that may be changed by compression or by loose wrapping. Measuring the roll itself makes sure we use the real thickness. So let’s do that!

Given the size of a full roll

We’ll turn that last idea into a formula with this 1999 question:

How Much Carpet is Left?

We use rolled carpet in our business and would like to know how much is left on a roll given the remaining diameter.

Given: Beginning OD, core OD, number of layers, length of roll, New OD

Find:  Length of carpet used or remaining.

There’s more information here than we need. We won’t be using the number of layers, but we’ll do that in the next answer.

Doctor Rick answered:

Hi, Zene, welcome to Ask Dr. Math.

I enjoy solving problems from the working world - students often ask us, "Will I ever have a use for this stuff?" The answer is, you'd be surprised how often math comes in handy at work.

Here is a method that will give an approximate length of the carpet roll; the thinner the carpet relative to the diameter of the core, the better the approximation.

Consider a cross-section of the roll. It is an annulus (like a washer - a disk with a hole in the middle). Its area is the area of the outer circle minus the area of the inner circle (the core).

Here is an annulus (yellow), whose area is \(\pi R^2-\pi r^2\):

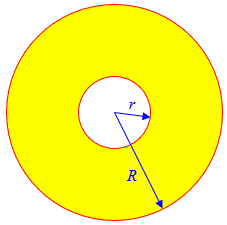
Let C be the core diameter, F the diameter of a full roll, and L the length of carpet on a full roll. Let's also define T, the thickness of the carpet.

The cross-section area of the full carpet is 

  Area = (pi/4)(F^2 - C^2)

(Read F^2 as F squared.) When you unroll the carpet, its cross-sectional area is LT (L times T). This area should be (approximately) the same as the area of the roll, so we can find the thickness T:

  T = (pi/4)(F^2 - C^2)/L

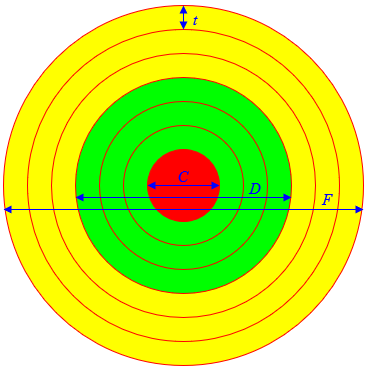
You can check the accuracy of the calculation so far by counting the layers of carpet on the full roll; this should be 

  n = (F - C)/(2T)
    = (F - C)L/((pi/2)(F^2 - C^2))
    = 2L/(pi(F + C))

You can also think of this calculation as dividing the length by the average circumference of a turn.

Now, if the diameter of a partial roll is D, we can use the same area calculations as above, but use the known T to find the length P of the carpet on the partial roll:

  P = Area/T
    = (pi/4)(D^2 - C^2)/((pi/4)(F^2 - C^2)/L)
    = L(D^2 - C^2)/(F^2 - C^2)

So there you have it. The length of carpet on a partial roll is the length on a full roll times the difference between the diameter squared and the core diameter squared, divided by the same calculation for the full roll.

This is $$P=\frac{L(D^2-C^2)}{F^2-C^2}$$ That’s nice: Divide the current difference of squared diameters, by the original, and you get the fraction of the roll that is left.

Given the number of turns

But there’s another way to avoid the sensitivity to the measured thickness, seen in this 2003 question:

Length of Coiled Belt

Working with conveyor belts we use a formula that gives a very close approximation of the length of a coil of belt, but I would like to know the reasoning of it. The outside and inside diameters of the coil (in inches) are added and then multiplied by the number of wraps, this is then multiplied by a constant (.1309), and the result is to be read in feet. 

It works, but I would like to know why. I tried to reason it out but I am stumped.

This turns out to be a valid formula: $$0.1309N(D+d)$$

I answered, starting with the formula we’ve seen:

Hi, Manny.

We have a number of answers to questions about the length on a roll of some material; one of them may give a formula like this based on the number of turns.

The cross sectional area of the coil is the difference between the circle formed by the outer diameter, D, and that formed by the inner diameter, d:

  A = pi (D/2)^2 - pi (d/2)^2 = pi/4 (D^2 - d^2)

The cross-sectional area of the belt straightened out is

  A = TL

where T is the thickness and L is the length. Setting these equal,

  TL = pi/4 (D^2 - d^2)

This is our basic formula.

But T can be found by dividing (D-d)/2 by the number of turns N:

  (D-d)/(2N) L = pi/4 (D^2 - d^2)

Solving for L,

  L = pi/4 2N (D^2-d^2)/(D-d)

Since D^2 - d^2 = (D-d)(D+d), this is

  L = pi/2 N (D+d)

That is your formula; to convert inches to feet we have to divide by 12, and (pi/2)/12 = 0.1309.

The calculation of T here is equivalent to the calculation of N in the previous answer. The new formula is $$L=\frac{\pi}{2}N(D+d)$$ using consistent units, and $$L=\frac{\pi}{2}N(D+d)\cdot\frac{1\text{ foot}}{12\text{ inches}}\approx0.1309N(D+d)$$ to get feet of length given diameters in inches.

Next time we’ll look at further variations in the question, focusing on how reality can change the formula.