Last time we looked at various ways to find tangent lines to a parabola without using calculus. Another standard calculus task is to find the maximum or minimum of a function; this is commonly done in the case of a parabola (quadratic function) using algebra, but can it be done with a cubic function? Yes, if you’re a little adventurous!
Here is a question from 2003:
Max and Min of Functions without Derivative I was curious to know if there is a general way to find the max and min of cubic functions without using derivatives. Our book does this with the use of graphing calculators, but I was wondering if there is a way to find the critical points without derivatives. Any help is greatly appreciated!
I don’t think I’d ever thought about this before, but ideas such as we saw last time suggested a way to do it. I replied:
Yes, there is a way, and it may be very instructive! Look at the graph of a cubic, and recall that if a polynomial has a double root, it will be tangent to the x-axis (at Q here):
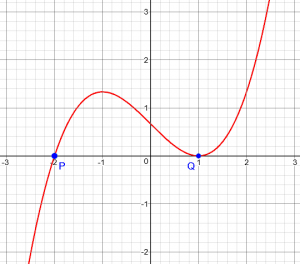
(A double root is one that corresponds to a squared factor.)
So given a general cubic, if we shift it vertically by the right amount, it will have a double root at one of the turning points.
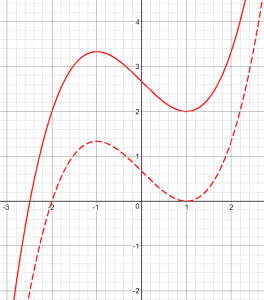
In this picture, the solid line represents the given cubic, and the broken line is the result of shifting it down some amount D, so that the turning point is on the x-axis. D, clearly, is the y-coordinate of the turning point.
So, given an equation y = ax^3 + bx^2 + cx + d any turning point will be a double root of the equation ax^3 + bx^2 + cx + d - D = 0 for some D, meaning that that equation can be factored as a(x-p)(x-q)^2 = 0
Our goal now is to find the value(s) of D for which this is true. We don’t yet know what p, q, or D might be.
(You might have been expecting us to use a discriminant. If so, think about why this is related to that idea …)
Buckle your seatbelt and hang on while we do some algebra:
Equating these and expanding, we have
a(x-p)(x-q)^2 = ax^3 + bx^2 + cx + d - D
a(x-p)(x^2 - 2qx + q^2) = ax^3 + bx^2 + cx + d - D
a(x^3 - (p+2q)x^2 + q(2p+q)x - pq^2) = ax^3 + bx^2 + cx + d - D
ax^3 - a(p+2q)x^2 + aq(2p+q)x - apq^2 = ax^3 + bx^2 + cx + d - D
The left-hand and right-hand sides must represent the same polynomial.
Since these must be equal for ALL x, we can equate coefficients:
a = a
-a(p+2q) = b
aq(2p+q) = c
-apq^2 = d-D
We have three equations (ignoring the first, which is simply the reason I multiplied my factored form by a in the first place) in three unknowns, p, q, and D, so we can solve to find the double root q, which is the location of the turning point.
Note that this is a system of non-linear equations, which many students are unfamiliar with; but they can be solved by substitution just like a linear system. Note also that D appears only in the fourth equation, so we will be leaving that for last.
To do this, we'll eliminate p by solving the second equation above for p:
p = -(b/a + 2q)
and putting this into the third equation:
aq(-2(b/a + 2q) + q) = c
This simplifies to
-2bq - 3aq^2 = c
3aq^2 + 2bq + c = 0
(Note that this is the derivative of the cubic we are working with. The rest of the work is just what we would do if we were using calculus, but with different reasoning.)
That was a surprise! We accidentally recreated the derivative (evaluated for \(x=q\)) without having slopes in mind at all. But this equation, as I said, is just what we’d have written using calculus, setting the derivative at \(x=q\) to zero.
Now we solve this for q using the quadratic formula:
-2b +- sqrt(4b^2 - 12ac) -b +- sqrt(b^2 - 3ac)
q = ------------------------ = ---------------------
6a 3a
This gives both turning points, since there are two ways to make a double root. Our last equation gives the value of D, the y-coordinate of the turning point:
D = apq^2 + d = -a(b/a + 2q)q^2 + d = -2aq^3 - bq^2 + d
= (aq^3 + bq^2 + cq + d) - (3aq^2 + 2bq + c)q
= aq^3 + bq^2 + cq + d
(since 3aq^2 + 2bq + c = 0), as we would expect given that x = q; so we don't really have to carry out this step.
Another surprise — or was it? Once we know q, we find the y-coordinate of the turning point just by evaluating the original equation at \(x=q\). We didn’t really need to use this fourth equation at all.
This is the sort of work that had to be done before calculus was invented. In many cases, calculus is really just a shortcut for algebra. Thanks for asking the question, because I'd never considered approaching it without calculus before!
Roy wrote back,
Thanks for the quick response, Dr. Peterson. That is just what I was looking for! I think my students will definitely benefit from seeing this approach and appreciate it once they get into calculus.
Repeated, concretely
Thirteen years later, Yousuf read that page, and wrote asking for clarification:
In [the conversation above], you said this:
Any turning point will be a double root of the equation
ax^3 + bx^2 + cx + d - D = 0
for some D, meaning that that equation can be factored as
a(x - p)(x - q)^2 = 0
The '- D' is a little confusing to understand as to where you got it from. How (or where?) did you obtain it to form that first equation? What significance does it play in this analogy?
I think I do understand the basic gist of what you're trying to achieve here. I understand the analogy that (I THINK) we picture first a general cubic graph which has no turning points touching the x-axis. If we can translate such a graph by the right amount vertically, what we get is a cubic graph where one of the turning points is touching the x-axis, making the axis a tangent to that point (we get a double root).
So with this said (daft as it may seem, but I may have answered my own question), is the 'D' the difference of the vertical component of the vector used to translate the general cubic graph to attain the second graph, which has at least one turning point on the x-axis?
People do often answer their own questions when they write them out! The fact that I hadn’t included the second picture above in the original probably accounts for his not having quite seen the point. I responded with such a graph to confirm his understanding.
But he wanted to see how it all works in a specific case, which is often a good idea:
For example, given a graph of x^3 - 7x^2 + 15x - 11. If we translated this graph using the vector (0, 2) -- so, 2 units in the positive direction of the y-axis, i.e., upwards -- we would get the equation
y = x^3 - 7x^2 + 15x - 9
= (x - 1)(x - 3)^2
Here, the double root emerges; and therefore, the x-axis is a tangent to the curve at x = 3, producing a minimum. Is the 'D' somehow tied into this analogy? Is D the difference between the original intercept of the graph (-11) and the translated graph (-9)? So would D (in this particular example) be -11 - (-9) = -2?
But having said all that, Doctor Math ... if the above analogy is correct, it was achieved through pure luck: I deliberately chose the equation (x - 1)(x - 3)^2, and just manipulated it. If we had such an equation as, say, x^3 - 7x^2 + 15x - 11, how would you know that translating it by 2 units upwards would achieve a similar graph containing a double root? and therefore a max/min point?
I'm really keen to understand if it is possible to calculate maximum and minimum points of cubic graphs WITHOUT the use of calculus. However easy it is, I want to explore this possibility.
I'd be most grateful if you would be able to please clarify this predicament.
Here is his function, before and after translating it upward:
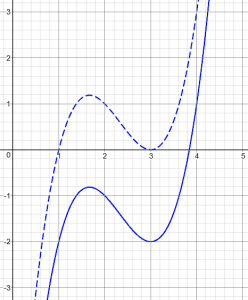
Like my graphs above, he worked backward to find a nice example, and wants to see the forward process actually carried out. I responded further:
Let's do it. The original conversation, above, answers your question didactically, showing how to find D ... eventually; but looking at it concretely would help anyone fully grasp it. We have the cubic equation y = x^3 - 7x^2 + 15x - 11 We translate this downward by an unknown distance D (the y-coordinate of the extremum in question), with the goal of having a double zero: y = x^3 - 7x^2 + 15x - 11 - D That is, we want, for some p and q, (x - p)(x - q)^2 == x^3 - 7x^2 + 15x - 11 - D Here, "==" represents "is identically equal to." That is, they must be equal for all x. Note that our "a" is 1.
So far, this is identical to what I did in the abstract. Our main goal is to find q, the x-coordinate of one of the turning points.
By the way, another way to say this is that we want to take this ... x^3 - 7x^2 + 15x - 11 ... and rewrite it as this: (x - p)(x - q)^2 + D
Now we dig into the algebra, which will be a little easier to follow with ordinary numerical coefficients:
We expand the left side, as I showed, resulting in
x^3 - (p + 2q)x^2 + q(2p + q)x - pq^2
== x^3 - 7x^2 + 15x - 11 - D
We conclude that we need
-(p + 2q) = -7
q(2p + q) = 15
-pq^2 = -11 - D
We solve the first equation for p:
p + 2q = 7
p = 7 - 2q
We put this into the second equation:
q(2(7 - 2q) + q) = 15
q(14 - 3q) = 15
3q^2 - 14q + 15 = 0
We solve this by factoring (since it has rational solutions, we don't need to use the quadratic formula):
(3q - 5)(q - 3) = 0
q = 5/3 or 3
This part was easier this time.
These will be the x-coordinates of the two turning points. To find the amount by which we have to translate to get x = 3, we put q = 3 and p = 7 - 2(3) = 1 into the last of our equations:
-pq^2 = -11 - D
D = pq^2 - 11
= (1)(3)^2 - 11 = -2
This tells us that our original equation ...
y = x^3 - 7x^2 + 15x - 11
... can be written as
y = (x - 1)(x - 3)^2 - 2
This last bit looks quite different from what I did in the general case, because I don't have crowds of letters everywhere and could use a different approach, which makes some parts feel more natural, but hides the fact that D = aq^3 + bq^2 + cq + d.
So we translated the graph up 2 units to touch the x-axis.
Now, the OTHER extremum is found by taking q = 5/3, so that p = 11/3. Then D turns out to be
D = pq^2 - 11
= (11/3)(5/3)^2 - 11
= 275/27 - 11
= -22/27
So we can also write our equation as
y = (x - 11/3)(x - 5/3)^2 - 22/27
You can check this out to see that it is true.
I hope that helps! It was interesting revisiting this old discussion and looking at it from a different direction.
Yousuf replied,
I want to say a HUUUGE thank you for helping clarify this article in the most subtle way. You explained it in the example and it all clicked in perfectly well. Now I can associate the points in the example seamlessly with the algebraic proof -- all thanks to your help!!
