(A new question of the week)
It’s surprising how many questions we get that end up being about problems that are poorly worded or simply wrong. But these can be as illuminating as good problems, by showing ways to catch the error. This is one simple in itself, but will lead us into a common question about the Side-Side-Angle case of triangle congruence.
A parallelogram proof
Here is the question, from October:
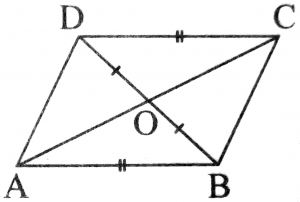
Question: In the figure, prove that ABCD is a parallelogram. Please….
My try:
To prove parallelogram, should show Angle BDC = Angle DBA (alternate angle) and if we are able to show them equal then AB will be parallel to DC and the line joining equal and parallel side are also equal and parallel. But how to prove them equal.
Is there any Method?
This is my try….
Statement Reason In Triangle ODC and OAB 1. DC = AB(s) given 2.DO = OB(s) given Only SS is possible for me. How to prove that ABCD is a parallelogram.
Yadav is following a good strategy, looking for a way to prove the conclusion (the last step), and then working backward. He sees that if he could prove AB and DC are parallel, then the conclusion would follow from a theorem about parallelograms; but he can’t find a way to get from the givens to that. Showing that triangles ODC and OAB are congruent would supply the needed congruent angles, but the only pairs of congruent parts he sees are two sides.
Examining the problem, I saw that he was missing something, but it was not sufficient:
Hi, Yadav.
Thanks for showing your thinking!
There is also an angle shared by the triangles ABO and CDO. This gives you SSA, which as you probably know does not necessarily imply congruence. I wonder if the problem didn’t say to prove it is a parallelogram, but to determine whether it is? Or were you told more than the picture shows?
I would look for a counterexample. Here are two examples of how to find one:
The SSA condition (Side-Side-Angle: two sides and a non-included angle being congruent) is, in general, not sufficient to prove congruence of triangles; in some cases you can in fact prove that the triangles are not congruent by making a counterexample, and in other cases additional data can make the proof possible. I didn’t yet know for sure that the claim was false (since all I knew was that I saw no sufficient basis to prove this congruence); but it was a reasonable thing to suggest.
Why Side-Side-Angle is not sufficient
Let’s take a look at SSA, first at why it doesn’t work, and then at the additions that can correct it. Then I’ll get back to this question.
Here is another question from our archives (1995), besides the two I referred to above:
Congruency Theorems for Triangles Given the three methods of proving two triangles congruent: SSS SAS ASA Using SAS, the angle must be a contained angle, Correct? Then, two triangles, one which has two sides that are of equal length to the second triangle, and both having an angle (not contained) equal, cannot be proved congruent. It seems to me that they are congruent, though. Any thoughts on this?
What looks right is not always right! Although in some cases it seems as if the SSA condition is sufficient, it is not always.
Doctor Ethan responded:
What you are looking for is an SSA postulate. I am afraid that it just isn't there. It is interesting to see why it can't be; and there are a few special cases in which it actually works. First let's look at one special case and then we'll look at why it doesn't work in general. Are you familiar with the HL postulate of congruency? It is for right triangles, and it says that if the hypotenuse and legs of two right triangles are congruent, then the triangles are congruent. That essentially is an SSA postulate, except that we require that the A be a right angle. I know that that is a pretty exclusive restriction, but we actually can get a little broader. Before I tell you how broad, let's look at a triangle for which it won't work.
(Ethan is calling these postulates; as I have previously discussed, in different systems they may be theorems, and it is probably better if only one is called a postulate. For our purposes, it doesn’t matter.) We’ll look later at how to make a valid SSA theorem; a counterexample of the basic SSA is the first task:
Here is an experiment for you to try. This should at least give you one example of a place that it won't work, and then you can write back with what you find out and I'll give you another hint about what you can try.
Get three sticks, one that is three inches long and two that are five inches long. Use them to make an isosceles triangle. It will look something like this:
/\
/ \
/ \
/ \
5/ \5
/ \
/ \
/ \
/________________\
3
Label them like this:
/\
/ \
/ \
/ \
a/ \c
/ \
/ \
/ \
/________________\
b
Now I want you to keep the angle fixed between a and c and move the stick of length 3 in until it forms a triangle again.
If you have followed these instructions, you have constructed two triangles that have congruencies SSA but are clearly not congruent triangles.
Roger apparently never replied, so Doctor Ethan didn’t get a chance to elaborate as promised. I will at least finish the counterexample. Here is the triangle he showed:
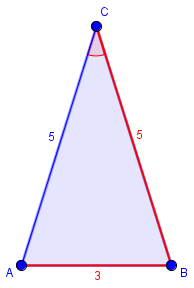
If the expected SSA theorem were true, then any triangle with the angle and sides marked in red would be congruent to this one. The challenge is, can we make a different triangle that fits those requirements? The answer is, yes: swing the 3-unit side around until it touches the blue side in a different place, like this:
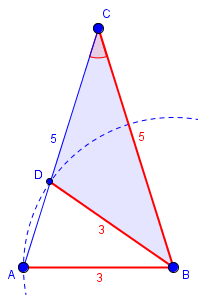The new triangle DCB is not congruent to ACB, though it has the same three red parts. This shows that the SSA conditions are not sufficient to prove congruence.
(Another student, Nathan, wrote in 1999 asking for the answer, and Doctor Rob provided a different example, with all integer sides, and showed how to make others. This is included in the same page.)
We have another such demonstration here:
Why There Is No SSA Congruence Postulate or Theorem
A counterexample for the parallelogram
Back to our original problem, Yadav wrote back answering my question:
Yes Sir. There was a question with a figure.
The question was:
- In the figure, AB=CD and BO=DO. Then prove that ABCD is a parallelogram.
What is the answer sir please reply me?
It appears to be definitely claiming that the statement is provable. Now, can we make a counterexample (so that we don’t need to try to prove the claim)? Or is it in fact true? I used those counterexamples to SSA as a model for what we needed:
The answer, as I suggested, is that ABCD is not necessarily a parallelogram. You can’t prove a false statement!
Here is a counterexample, in which the conditions are met but the conclusion is false. Did you read the links I provided, and trying doing what they said?
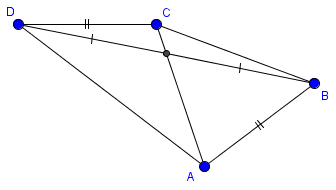
Here, ABCD is a quadrilateral with AB = CD and BO = DO. But it is not a parallelogram, so the claim is false.
Here is how I constructed my counterexample; you should be able to see its inspiration:
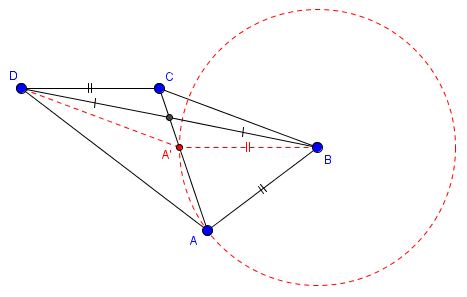
I first made a parallelogram A’BCD, then swung A’ in a circle to find A (which required moving parts around until that circle met line A’C as needed). As a result, triangles ODC and OAB are not congruent (as ODC and OA’B are), so AB is not parallel to DC.
You may notice that in the figure originally given, this can’t happen because of the particular angles used; that could either be intentional, to make it harder for the student to discover that the theorem is false, or accidental, the reason its creator didn’t realize it.
Salvaging Side-Side-Angle
Let’s get back to SSA. What additional conditions would it take to make a valid theorem? This is something Doctor Ethan said he would talk about, but never got the chance.
Here is a question from 2001, asking about such a valid theorem:
SSA Proof How do I prove the hypotenuse-leg congruence for triangles? My professor suggested using the S.S.A. theorem
The HL theorem, as Doctor Ethan mentioned, is a special case of SSA, where the two sides are the hypotenuse and a leg of a right triangle, and the angle is the right angle. This professor is evidently referring to some form of SSA theorem that is valid; what is it?
Doctor Rob discussed such a general theorem:
If two triangles have one angle, one adjacent side, and the opposite side equal, then they may or may not be congruent. That means that using S.S.A. is tricky. Suppose, for example, you were given acute <A and sides b and a. Then the picture might look like this:
This is how you might start out drawing a triangle, given its ∠A, b, and a (not yet drawn).
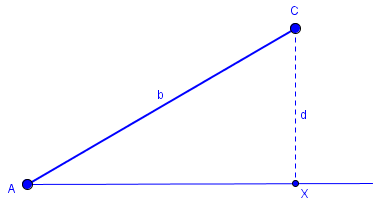
If you know some trigonometry, you'll realize that d = b*sin(<A). Now draw a circle with radius a and center C. Point B must lie on line AX and on the circle. There are several cases: Case 1: a < d. The circle and line don't intersect, and there are no triangles with these parameters.
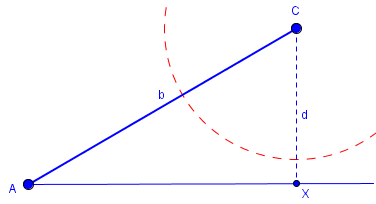
Note that this case will never occur in congruence proofs, because neither triangle exists!
Case 2: a = d. The circle and line are tangent at X, so B = X, and there is just one triangle with these parameters. In this case, <ABC is a right angle.
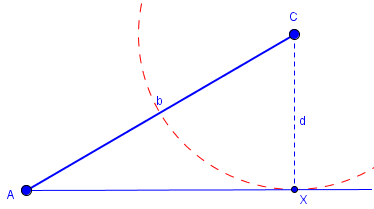
This case will not show up in the typical proof, because it requires information about the relationship between S, S, and A that requires either knowledge of the other angle, or of trigonometry.
Case 3: d < a < b. The circle and line intersect in two points B and B', with B' between A and X, and B to the right of X. Now there are two triangles with these parameters, ABC and AB'C, and you can't prove congruence.
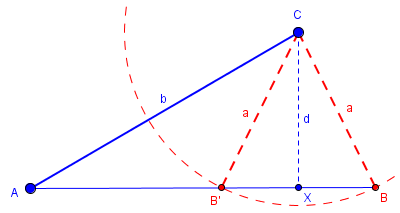
This is often called the “ambiguous case” in trigonometry, and is like our counterexamples above.
Case 4: b <= a. The circle and the line intersect in two points B and B', but B' is at or to the left of A, so the angle drawn above is an exterior angle to that triangle. Thus there is just one triangle with these parameters, and you can prove congruence.
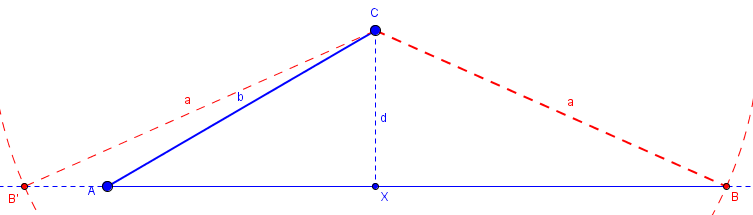
These cases all assumed that ∠A is acute.
If <A is a right angle, and so d = b, the following cases hold: Case 5: a <= b. No triangle.
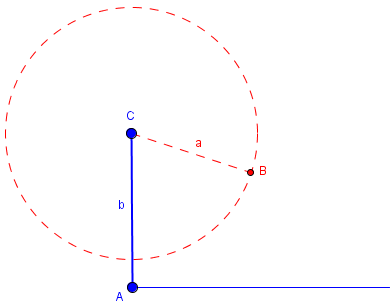
Case 6: b < a. There is just one triangle, and you can prove congruence.
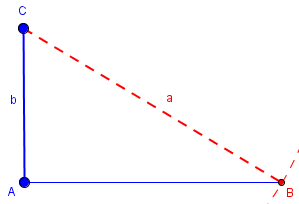
This is the HL case.
If <A is obtuse, then following cases hold: Case 7: a <= b. No triangle.
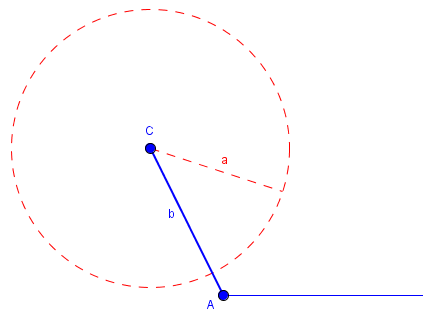
Case 8: b < a. There is just one triangle, and you can prove congruence.
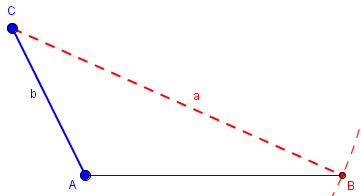
Thus the theorem should say, THEOREM (S.S.A.): If two triangles ABC and DEF have BC congruent to EF, AC congruent to DF, and <A congruent to <D, then: 1. if AC >= BC, the triangles are congruent. 2. if BC = AC*sin(<A), then the triangles are congruent. 3. if AC*sin(<A) < BC < AC, then the triangles may or may not be congruent. In your case, you know that the hypotenuse AC is longer than either leg, including BC, so Part 1 of the above theorem applies.
So, in order to apply SSA to our parallelogram proof, we would need to know that AB > OB (as in the original picture), or that \(\displaystyle \frac{\ \overline{AB}\ }{\overline{OB}} = \sin(\angle AOB)\).