Last time we looked at how to find the length of material on a roll, making some necessary simplifications. Here, I want to look at some variations on that: first, about carpet in particular, and then about wire on a spool.
How does a carpet really bend?
First, a question about carpet from 2008:
Finding the Length of Carpet Left on a Roll I can see the end of a roll of carpet and figure out the approximate square yardage by taking the inside circumference, outside circumference and number of total layers left. I need to see if there is a formula. EX: 12"=inside roll circumference, 24"=outside roll circumference, 12 layers on end of roll. The difference between 24" and 12" is 12", so each layer must be about 1" more than the previous layer (i.e. first layer length = 12", 2nd = 13", 3rd = 14" . . . 24th = 24"). Now, when I add all layers together I get a certain total length. What is the equation for such a problem?
Last time we got a formula using the number of turns and diameter; here we have circumferences rather than diameters. Lee suggests using series, which we also tried last time.
I answered Lee:
We have many answers to this kind of question; you might try searching our archives for the phrase "roll of carpet" to find those that happen to be about carpets.
Here is one, with references to others:
Determining Length of Material Remaining on a Roll
http://www.mathforum.org/library/drmath/view/67031.html
My formula there is
L = pi/4 (Do^2 - Di^2)/t
where
Do = outer diameter
Di = inner diameter
t = thickness of one layer
Now we have to adapt it:
You give the circumferences, which we'll have to divide by pi, and since you know the number of layers, we can make a different formula based on a number of layers N.
Let's say we have
Co = outer circumference [so Do = Co/pi]
Ci = core circumference [so Di = Ci/pi]
N = number of layers [so t = (Do-Di)/(2N) = (Co-Ci)/(2 pi N)]
Then my formula becomes
L = pi/4 (Co^2 - Ci^2)/(pi^2) * (2 pi N)/(Co - Ci)
= (Co + Ci)*N/2
For your numbers this gives
L = (24 + 12)*12/2 = 216 inches
This is essentially the same as the last answer given last time, but using circumference rather than diameter: $$L=\frac{1}{2}N(C_o+C_i)$$
What about his series approach? There’s a little problem there, that will lead to a new idea:
This is exactly what I would get as an approximation using your idea of the linear increase in circumference with each layer. The sum of an arithmetic series like your 12 + 13 + 14 + ... + 23 (note that you counted 13 layers by including both 12 and 24) is the average of the first and last, times the number of terms. In your example, this is 12*(12+23)/2 = 210 inches. But what about the last layer? We only got to a length of 23. If we split the difference and treat the series as 12.5 + 13.5 + ... + 23.5, our length turns out to be 12*(12.5+23.5)/2 = 216. And in fact, we could derive the formula above starting with this idea of the arithmetic series.
He had too many layers, by counting both the inside and outside circumferences. But counting only the 12 layers this way leads to a too-small answer – or does it?
Here I made the adjustment we made in our series derivation last time, by treating the length of a layer as the circumference in its middle. This approach amounts to assuming the carpet bends in such a way that the inside compresses and the outside expands (as if there were an incompressible layer in the middle):
![]()
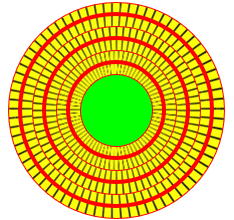
This might apply to, say, a foam mat being rolled up. But this led me to a new speculation:
Actually, I suspect that in the case of carpet it is possible that the backing would be more rigid than the top, so that the actual length would be better estimated by the 210 inch figure; my 216 assumes that the outside of each layer expands and the inside contracts equally when it is rolled up. The formula using your idea turns out to be
L = (Co + Ci - (Co - Ci)/N)*N/2
= ((N-1)Co + (N+1)Ci)/2
I've never looked at it from this perspective before and obtained this particular formula! It's not quite as simple, and considering that the carpet really forms a spiral rather than neat layers, it's still just an approximation; but it has an interesting "elegance"!
Picture the carpet this time with an incompressible backing on the inside of the roll, the rest being expandable fibers:
![]()
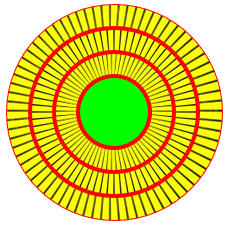
To get this formula, we can take the total length as the sum of the inner circumference of each layer. The first layer has length \(C_i\), and the last is \(C_i+(N-1)\frac{(C_o-C_i)}{N}=\frac{NC_i+(N-1)(C_o-C_i)}{N}=\frac{C_i+(N-1)C_o}{N}\). The sum of these N terms is N times the average of the first and last terms: $$L=\frac{N}{2}\left(C_i+\frac{C_i+(N-1)C_o}{N}\right)\\=\frac{N}{2}\left(\frac{(N+1)C_i+(N-1)C_o}{N}\right)\\=\frac{(N+1)C_i+(N-1)C_o}{2}$$
This formula amounts to averaging the inner and outer circumferences (as in our final formula last time), but weighting the former more heavily than the latter. Using Lee’s numbers, it gives $$\frac{(11)24+(13)12}{2}=210$$ as we found before.
On the other hand, in editing this, I realized that carpet is commonly rolled with the backing on the outside! That makes sense for several reasons. In this case, the formula becomes $$L=\frac{(N-1)C_i+(N+1)C_o}{2},$$ with the outside given greater weight.
Wire on a reel
Now consider this question from 2001:
Calculating the Length of String on a Reel What is the formula for calculating the length of wire that can go on a reel (spindle) where the reels may have different diameters, hub diameters, and widths, and the wires may have different diameters?
This is like the carpet problem, except that each layer is made up of many wires side by side.

I answered:
Hi, Larry. The answer will be similar to that for a similar question we have answered many times, about the amount of material (such as carpet) on a roll: How Much Carpet is Left? http://mathforum.org/dr.math/problems/gillette.03.27.99.html We find the length by equating the volume of material on the roll to its volume laid out flat.
There we talked about the cross-section area, but we could just as well multiply everything by the width to get volumes. With wire, we need to.
There is always a caveat in this calculation, however: we have to assume that the material retains the same thickness as it bends around the roll, and is not either compressed or wound loosely. The calculation is very sensitive to the actual thickness of the material on the roll. The same is even more true in your case. The wire may be wound in different ways that will incorporate different amounts of air space between turns, so it is hard to be sure how much of the volume on the reel consists of wire. The best thing to do would be to measure an actual reel of known length in order to determine this ratio and adjust the formula, rather than blindly trust theory.
This is something we did in the last couple explanations last time. It’s easy to picture winding up the wire very carefully and tightly, or very haphazardly and loosely, giving different amounts in the same diameter. Here, we’ll assume the tightest possible case, and then multiply by a factor to account for reality.
Having said that, let's look at the problem. For simplicity, I'm going to pretend that the wire has a square cross section, since then there would be no need for space between turns. Your measurements will determine how closely this corresponds to reality.
Suppose the reel has hub diameter Di, outside diameter Do, and width W. Then the volume of wire on it is
V = pi(Do^2 - Di^2)W/4
Suppose you have a wire with length L and square cross-section with side Dw (the diameter of the wire). Its volume is
V = LDw^2
Setting these equal, we get
LDw^2 = pi(Do^2 - Di^2)W/4
and we can solve to find
L = pi(Do^2 - Di^2)W/(4Dw^2)
This is the ideal case: $$L=\frac{\pi(D_o^2-D_i^2)W}{4D_w^2}$$
Now suppose you measure an actual reel, and the actual length is X times this calculated length (let's hope not too far from 1). Then you can take X as the typical correction factor, and multiply any calculated length by X to estimate the actual length when you don't know it ahead of time. This correction factor may well be more or less constant for all reels wound by the same method.
If you have questions, they may be answered below.
Reconstructing a handbook formula
A 2003 question asks about a different formula:
Length of Cable on a Reel What is the formula used to determine the length of cable on a reel? Specifically the way to determine the "k" factor if I use the formula L = A*(A+B)*C*k where L = length of wire (in feet) A = diameter of wire (in inches) B = diameter of drum (in inches) C = width of drum (in inches) k = some empirical factor. If I were going to just run a bunch of iterations (can't find k value), and if I were using a 30-inch drum 30 inches wide and winding 2.5 inch cable, would I determine the length of the first layer using a diameter of 30 inches or 31.25 inches (half of the wire diameter)? What do I use for a k value? (My reference book only goes to 1.5" diameter.) What do I use for the initial diameter? If I use a 30"x30" drum and 2.5" cable and run three iterations starting with the first "layer" diameter of 30", I can get 329.87' of cable in three layers. But if I start with a diameter of 31.25" I can get 353.43' of cable in three layers. Which method is correct?
It will turn out that the definition of A is misleading, so we’ll have to clear that up. Skip down to the bottom to see what he really means!
But note that he is doing some good thinking, akin to what we did above, in working out a series derivation of the carpet formula, wisely pondering whether to use the inner radius or the middle radius for each layer.
I answered again:
Hi, Joe. Your formula seems very odd; for example, if you increase the diameter of the cable, that should decrease the amount that will fit on the reel, yet your formula shows an increase. Did you copy the formula and definitions right? Ah! Looking closer at your discussion, I realize that your "diameter of wire" is apparently not the diameter of the cable itself, but the outside diameter of the full reel, while "diameter of reel" is the size of the core around which it is wound. Your "k" apparently incorporates the diameter of the cable, so you have to look it up in a table rather than include the cable diameter in the formula.
This suggests that Joe’s A, B, and C are our \(D_o\), \(D_i\), and \(W\), respectively, and k is a function of \(D_w\). But it will turn out to be a little different.
I referred to the answer above:
The formula I came up with there is L = pi(Do^2 - Di^2)W/(4Dw^2) where L = length of wire (all measurements in the same unit) W = width of reel Di = diameter of core Do = diameter of full reel Dw = diameter of wire As I suggest there, you will probably have to multiply by an arbitrary factor that depends on the nature of the wire and the way it is wound, but will not vary (much) for different sizes of reel and perhaps of wire.
This repeats what we said above. Can this be put into Joe’s form?
Using your variables, plus "d" for the diameter of the wire itself, this would be
L = length of wire (in feet, requiring division by 12 below)
A = diameter of full reel (in inches)
B = diameter of drum [core] (in inches)
C = width of drum (in inches)
L = pi/12 (A^2 - B^2)C/(4d^2)
= pi/(48d^2) (A - B)(A + B)C
Comparing this to your
L = A*(A + B)*C*k
it seems that you are not subtracting B from A (or else I am still misunderstanding what A is), and that k = pi/(48d^2) times whatever adjustment factor is necessary to account for space between turns.
Comparing the forms, you might be able to guess that \(A-B\) is somehow incorporated into the actual meaning of A. We’ll find that to be true.
Using your example, my formula would give, for a 30-inch by 30-inch reel holding three layers of 2.5-inch cable (so that the outer diameter A is 30+6*2.5 = 45), L = pi/(48*2.5^2) (45-30)(45+30)30 = 0.01047*15*75*30 = 353.4 ft If that is not reasonably close to what you actually measure, I would recommend winding several layers, and then use the ratio of the actual length to the calculated length as an additional factor in the equation, in order to make it more realistic.
Not quite.
Why squares?
Joe replied:
Thanks for your help. To clear up what A is. A = 1/2 thickness of all of the wire from the outside of the hub, or the radius of thickness of the wire wound on the drum, or the outside radius minus the drum radius. I got this formula from a pocket reference book; however, the k values they use don't go high enough for my application.
I’ll incorporate this into the formula soon, but Joe had a further question that I answered first:
I understand your formula and agree with your conclusions. However, I have one more question. When you set the volume of the wire equal to the square of the wire thickness dw^2, (assuming a square cross section) the formula works. But if you use the actual circular cross sectional area (pi*r^2)*length of wire and set that volume equation equal to the first equation the answer is wrong. Why do you assume a square cross-section when in actuality it isn't square but rather a circle?
I responded:
Hi, Joe.
I assumed a square cross-section in order to include both the wire itself and the air around it, supposing that the wires lie in this pattern:
***** ***** *****
** ** ** ** ** **
* * * * * *
* * * *
* * * * * *
** ** ** ** ** **
***** ***** *****
** ** ** ** ** **
* * * * * *
* * * *
* * * * * *
** ** ** ** ** **
***** ***** *****
** ** ** ** ** **
* * * * * *
* * * *
* * * * * *
** ** ** ** ** **
***** ***** *****
and not, say, this:
***** ***** *****
** ** ** ** ** **
* * * * * *
* * * *
* * * * * *
** ******* ******* **
****** ******* ******
* * * *
* * *
* * * *
****** ******* ******
** ******* ******* **
* * * * * *
* * * *
* * * * * *
** ** ** ** ** **
***** ***** *****
That is, the assumption we made is that the wires are arranged like this:
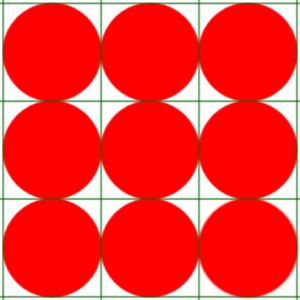
while they could be arranged more tightly as
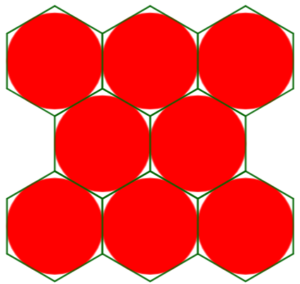
In the former case, each circle can be thought of as included in a square that fits with those around it, filling the whole space. In the second picture, we would have to use hexagons, and then we would still be missing some air at the top, bottom, and sides.
There’s also another effect here. In the second form, the distance between centers of wires in successive layers, rather than \(D_w\), is \(\frac{\sqrt{3}}{2}D_w\approx0.866\):
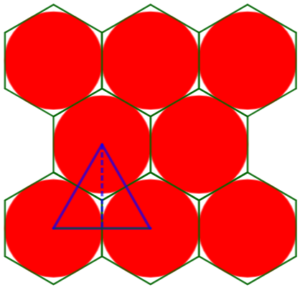
This makes the layers closer together.
So, ignoring the effects at the ends of layers, our answer would be multiplied by about \(\frac{4}{3}\):
$$L=\frac{\pi(D_o^2-D_i^2)W}{4\left(\frac{\sqrt{3}}{2}D_w\right)^2}=\frac{\pi(D_o^2-D_i^2)W}{3D_w^2}$$
But in reality, wires probably lie less neatly than the square arrangement, rather than more, so the actual length would be smaller.
In any case, apart from edge effects that would make our formula inaccurate for small amounts of wire, we are really just multiplying the circular cross-section by some factor related to how the wires lie, which we really have to adjust at the end anyway, since nothing works as well in reality as in the mathematical approximations we're using. The square assumption just keeps things simple.
So the factor k will adjust for whatever the reality is, and, as Joe stated, has to be determined empirically (that is, by measuring actual reels of wire).
Finalizing the formula
Now, let’s get the formula right:
I was wondering if your A might be my (Do - Di); but your calling it a "diameter" kept me from considering that it might be, as you now say it is, (Do - Di)/2. Then my Do - Di is your 2A and my Do + Di is your 2(A+B) [that is, Do + Di = (Do-Di)+2Di = 2A + 2B], so my formula using your variables is
L = length of wire (in feet, requiring division by 12 below)
A = thickness of wire on reel (in inches)
B = diameter of drum [core] (in inches)
C = width of drum (in inches)
L = pi/12 (Do - Di)(Do + Di)W/(4Dw^2)
= pi/12 2A 2(A+B) C/(4d^2)
= pi/(12d^2) A(A+B)C
and your k is pi/(12d^2), times any adjustment factor you need. I'm curious to see how their k's agree with this, and whether they adjust it using more than just a constant factor.
In any case, it sounds like we've got it figured out.
So the formula is now $$L=\frac{\pi}{12}\cdot(D_o-D_i)\cdot(D_o+D_i)\cdot\frac{W}{4D_w^2}\\=\frac{\pi}{12}\cdot2A\cdot2(A+B)\cdot\frac{C}{4d^2}\\=\frac{\pi}{12d^2}A(A+B)C$$ So k is some multiple of \(\frac{\pi}{12d^2}\).
Real-life details
Joe added:
Thanks for all your help, I agree with your version of using a square cross section to include the air spaces. If you're still interested, the k values from the table are .25" = 3.29 .5" = 0.925 .75" = 0.428 1" = 0.239 1.25" = 0.152 1.5" = 0.107 1.75" = 0.0770 Thanks.
Putting this into a spreadsheet to compare it to my “k“, we see this:
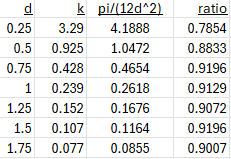
I closed:
Thanks. It looks as if their k is about 0.9 times mine, slightly more for the smaller wire sizes. It makes sense that this is less than 1, since you would want to allow for non-optimal layering, which would fit less cable in the same space. You may want to multiply my formula by about 0.9 to be consistent, and then check the results against reality.
So our final formula, at least for larger wire, is $$L\approx\frac{0.075\pi}{d^2}A(A+B)C$$ where, again, A is the thickness of the wire around the reel, B is the diameter of the reel, and C is the width of the reel, while d is the diameter of the wire. Actual results depend on how the wire is wrapped, and would probably vary according to the width and number of layers, not just the diameter of the wire.
And, to repeat our original version of the formula with this 0.9 multiplier, $$L\approx0.9\frac{\pi(D_o^2-D_i^2)W}{4D_w^2}\approx\frac{0.7(D_o^2-D_i^2)W}{D_w^2}$$
In editing this, it occurred to me to search for a source of this formula and the table of k; surprisingly, after 21 years, I found one. Here is the equivalent formula and table from this site:
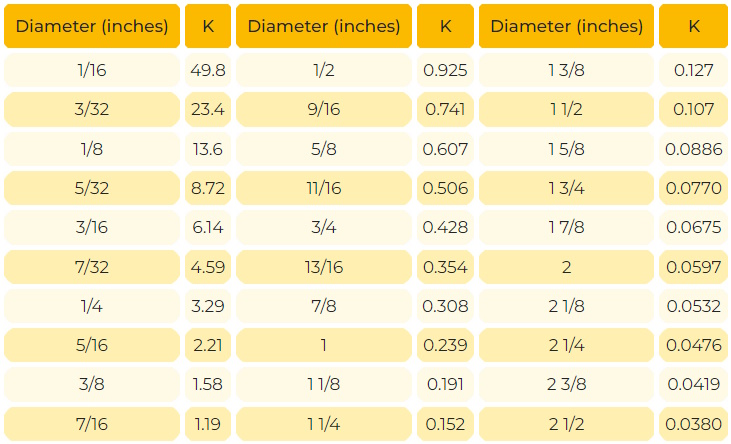
The numbers agree with Joe’s table, where the diameters match. Here is the table comparing these with my k:
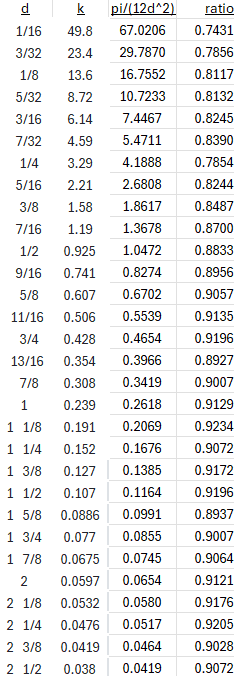
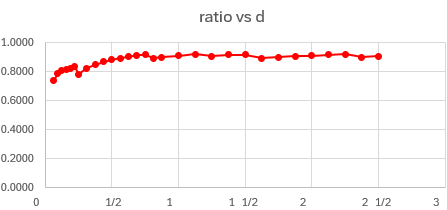
But why would the thinnest wire require a smaller multiplier, so that less wire fits in a given space than we expect in theory? I would expect that there is less of an edge effect when more strands fit in one layer, but that would imply it can be wrapped better, and more would fit. Math can’t always explain the details of reality!
