We’ll be looking at various aspects of place value, starting here with the basic concepts. As soon as you learn to write numbers beyond 10, you have to start understanding this concept; so we have to begin at a concrete level and move gradually to something more abstract.
Place value for children
Our first question comes from a mother in 2007:
Introducing Place Value to Children I'm wondering how to teach my son about place value. How can I show him that units are up to 9 then when it comes to 10 is tens and so on? I really get confused myself how to explain it to him. 1,2,3,4,5,6,7,8,9 are ones 10,11,12,13,14,15,16, up to 99 is tens and so on
So, what does it mean to talk about tens, and how can we make it meaningful to young children?
I answered by referring to my own experience with my homeschooled kids, since I am not an elementary teacher:
Hi, Auria. I introduced place value to my children with several different models. One was beans, cups, and trays: I would put 10 beans in each cup, and 10 cups on a tray, while counting beans. Thus up to 9 would just go on the table, individually; when there were 10 they would fill a cup, and then I'd keep putting more on the table until there were another 10. Eventually I might have 1 tray of 10 cups (100 beans), and 3 additional cups (30), and 7 single beans, for a total of 137. The hundreds place represents the number of trays (1), the tens place the number of cups (3), and the ones place the number of single beans (7). This makes it clear that any numeral represents a number we can count, and any number of beans can be expressed this way. You can also do addition and subtraction with this system, and see how the digits work.
Here is my representation of 137 beans:
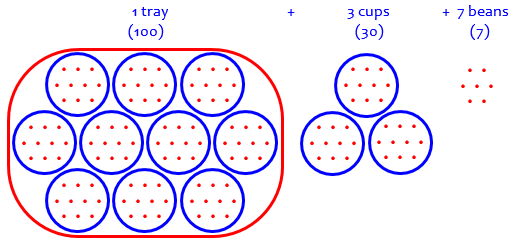
To count beans, we put them individually on the counter (!), and as soon as we have 10 of them, we put them in a cup so we have “1 cup and 0 [extra] beans”, or “10”. Then we keep placing more beans until we get 2 cups (“20”), and so on. The end result can be called “one hundred, three tens, and 7 ones (or units)”; this is what “137” means. This is about as concrete and tangible as you can get in math.
The nice thing here is that, unlike some other representations, we are simultaneously representing the numeral “137”, and showing 137 individual beans!
There are also manipulatives you can buy (base ten blocks) that represent different numbers of little cubes (“units”), rows of ten (“rods” or “longs”), and squares of a hundred (“flats”), and even big cubes of a thousand (“cubes” or “blocks”):
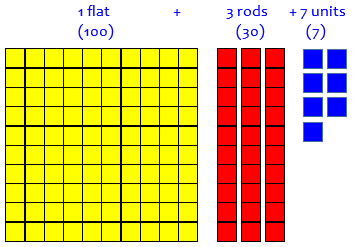
These are only slightly less “real”, because they are stuck together, not made of separate bits.
Another model was play money, which is a little more abstract so it should be used after the beans are fully understood. A $10 bill represents a stack of 10 $1's; a $100 bill can be exchanged for a stack of 10 $10's, or 100 $1's. By always having no more than 9 of any one kind of bill, we represent a number's places, and can do addition and subtraction as with the beans. Our number 137 would be one 100, three 10's, and seven 1's. To add $84 to that, I would add 4 more $1's, but since I have 11 now and that's too many, I change 10 of them for a $10 and keep only 1 $1 in the pile. Now I have 3, plus 8, plus the new 1 $10's, for a total of 12 $10's; again I change 10 of those for a $100, leaving me with a total of 2 $100's, 2 $10's, and 1 $1.
Now we don’t actually have 137 dollar bills in front of us, but something that represents it:
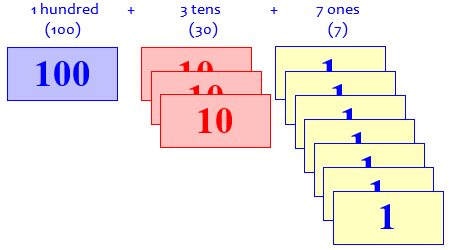
The restriction to no more than 9 per place is just a matter of using as few bills as possible.
(By the way, to introduce base 5 numerals, you can use pennies, nickels, and quarters.)
Another thing that was of interest was a mechanical counter, either one that works like an old odometer (if you can find anything like that any more), or the plastic counters they used to have where you could click any digit to add one. I don't know if anything like this can still be found easily!
On the right is what I described, actually used for keeping track of money; on the left is a hand tally counter you can still get:

The physical action can make the idea of counting, especially moving from 9 to 0 and “carrying” to the next digit, more concrete, even though the representation is now entirely abstract.
Why stop at 9?
A 2002 question touched on that very thing: Why can’t a digit be more than 9?
Place Value and the Number Nine I am asking this for my 10-year-old grandson. Why is 9 the largest number you can put into any place value spot?
I answered:
Hi, Jacques. The base-ten system is built around the idea that you can name every number by counting tens. Once you have ten tens, you give it a new name (hundreds) and write it using the hundreds place. When you get ten hundreds, you give that a new name (thousands) and use the thousands place. You never need to write a digit larger than 9, because ten of anything gets a new name. Suppose we did use ten as a digit. We could talk about the number "tenty," meaning ten tens, and write it perhaps as X0, using X as the symbol for the digit ten. That would really be the same as one hundred; since we already have a name for it, it would be redundant. So we don't need an extra symbol for ten; X is written as 10, and X0 as 100.
We want to give every number a unique name, so we don’t need a symbol (like “X”) for ten, because “10” handles it. The counter might be a particularly good way to illustrate this.
But occasionally you will see such ideas used humorously. In _The Lord of the Rings_, the story begins with Bilbo Baggins' "eleventy-first birthday." That would mean eleven tens and one, or 110+1, which is really 111. Again, we have a way to say it without using "eleventy," so we don't need to use eleven as a digit.
The fun part is that we can actually understand what this would mean, even though we don’t use it!
Place value for adults
It is not only children who need help understanding all this; adults can be helped by concrete explanations as well as abstract considerations. For this question, from 2000, I used the former:
Explanation of Place Values I guess this is a bit philosophical, but here it goes. It is written that as you progress from the units place to the tens place to the hundreds place, the value is increasing ten times the numeral on its right. For example, in 589 the 8 is ten times greater than the 9 and the 5 is ten times greater than the 8. How does this increase by ten times work out? If you count from 1 to 10 I imagine that you are ten greater than nothing or 0 (which is a place holder). Then you count 10 ten times to reach 100 but you must also count from the number 10 up to 100. What that means is that 100, which is 10 times the number 10, also must include the 10 as the beginning of the counting. Can you explain to me on a deeper level what is going on?
It wasn’t quite clear how Enzo was thinking. I answered by first relating place value to units of measure:
Hi, Enzo. What increases at each digit is the granularity of the count - the size of the unit we are counting with. It's similar to measuring a distance as, say, 5 miles, 8 feet, and 9 inches. As you go several miles, each mile includes every foot you have gone along the way, EXCEPT for the last few, which were not enough to make a full mile. In the final measurement you give, the 8 feet are not part of the 5 miles you counted, but are the leftover feet that were not part of any full mile.
This is much like those 7 leftover beans that were not in a cup (not part of the tens).
I next, in effect, used base ten blocks to illustrate, but expressing it more like cups and trays, counting individual objects:
Similarly, each digit counts a different size group. If I say I have 589 objects, it means I can count by 100's until I have 5 of them, with less than a hundred left; then count by 10's until I have 8 tens, with less than ten left; and then count what's left by 1's, finding 9 of them. We can picture this as putting them into packages of decreasing sizes; there are ten tens in a hundred, and ten units in a ten, package inside package; when there are not enough to fill another package of one size, we start using smaller packages to use up the remainder:
500
+-----------------------------------------+
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
+-----------------------------------------+
+-----------------------------------------+
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
+-----------------------------------------+
+-----------------------------------------+
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
+-----------------------------------------+
+-----------------------------------------+
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
+-----------------------------------------+
+-----------------------------------------+
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| |*| |*| |*| |*| |*| |*| |*| |*| |*| |*| |
| +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ |
+-----------------------------------------+
80
+-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+
|*| |*| |*| |*| |*| |*| |*| |*|
|*| |*| |*| |*| |*| |*| |*| |*|
|*| |*| |*| |*| |*| |*| |*| |*|
|*| |*| |*| |*| |*| |*| |*| |*|
|*| |*| |*| |*| |*| |*| |*| |*|
|*| |*| |*| |*| |*| |*| |*| |*|
|*| |*| |*| |*| |*| |*| |*| |*|
|*| |*| |*| |*| |*| |*| |*| |*|
|*| |*| |*| |*| |*| |*| |*| |*|
|*| |*| |*| |*| |*| |*| |*| |*|
+-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+
9
*
*
*
*
*
*
*
*
*
Here, starting from the given number 589, I counted in decreasing sizes, using up digits from left to right, resulting in the static image of the final result. This is the opposite of the process of counting, which he used in his own example, so I described that more fully:
When we count by ones up to 589, as you discussed, we have to constantly change smaller groups for larger ones. Each time we reach a multiple of ten we repackage them as a single ten, with no individual units left. This is what happens when we change from 9 to 10 or from 289 to 290, setting the units place back to 0 and adding one to the tens place. Each time we reach a multiple of 100, we package our last ten 10's as a single hundred, clearing the other digits, as when we go from 99 to 100 or from 299 to 300. Each place thus incorporates whatever was counted before, taking over what had been in the lower digits. This process can be seen in an odometer, where each numbered wheel counts the number of times the wheel to its right passed 9 and returned to 0.
The odometer, again, is a mechanical representation of the result, but considerably more abstract.
So yes, the 5, which represents 5 hundreds, includes the first ten you counted; it starts at zero, not after the first ten. Yet the 500 does not include the 80 or the 9. When you count starting with the larger units as I did above, you see more clearly that the smaller units are OUTSIDE the larger units, but it really works the same either way. I hope this clarifies what place value is all about. Talking about counting and packaging doesn't sound like a "deeper level," but I think it shows what we mean more clearly than deeper math would. Let me know if you want a more advanced perspective on this.
Next, we’ll move on to what might be considered that deeper, abstract level, looking at a written number and seeing what it means without counting anything.
Breaking a number down
Here is a question from a 12-year-old in 2003:
Decoding Place Value What does it mean to be in base 10? What does the 1 represent? What does the 0 represent? I think I understand the 1 to represent one 10, but I'm a little confused about the 0. Does it mean that there are no units left over from base 10?
Doctor Ian answered, using a more interesting example:
Hi Samantha,
When we write a number like
2034
each digit is multiplied by some power of 10, and the results are added up. That is,
2034 = 2*1000 + 0*100 + 3*10 + 4*1
^ ^ ^ ^
| | | |
2 groups 0 groups 3 groups 4 groups
of 1000 of 100 of 10 of 1
| | | |
| | | |
2000 <-- | | |
000 <------------- | |
30 <------------------------ |
+ 4 <-----------------------------------
------
2034
Does this help?
This is called expanded notation, and is another way to say “2 thousands, 0 hundreds, 3 tens, and 4 units”. But now it’s become an abstract process of writing a sum of multiples of powers of ten.
Naming a place using powers of ten
This 2003 question is from another 12-year-old, who would be ready for a bigger picture, even though the question in itself doesn’t require it.
Which Place? In which place is the digit 6 in the number 3164297 ? In my book there is an answer that says it is in the 100000, and when I asked my mom she said 10000. I don't know which one is correct!
The quick answer would be, “You’re right and the book is wrong.” But that begs the question, “How do you know you’re right?” Doctor Ian answered:
Hi Kelly, One way to solve a problem like this is to write down all the possible place values. We do that by starting with 1, and multiplying by 10. 10,000 1000 100 10 1
Those are the place values, in order (which is why he started at the right). The fifth, fourth, third, second, and first places from the right are, respectively, the
ten-thousands … thousands … hundreds … tens … ones (units)
places. To handle big numbers, he introduced the idea of exponents, in case Kelly wasn’t familiar with them, and then continued:
Why am I telling you all this? Because now we can find the place value of each digit in a number like 3164297 by using exponents:
6 5 4 3 2 1 0
10 10 10 10 10 10 10 <- place values
3 1 6 4 2 9 7 <- digits
So to find the place value of a digit, we count over from the right, starting at 0:
3164297 <- digits
^
| 0
| 1
| 2
|3
4 <- counting from zero
When we get to the digit 6, we're at place 4; so the place value of 6 in this number is 10^4, which is 1 with 4 zeros, or 10,000.
So you and your mom are correct.
To put it a little differently, to find the place value of the 6, you can write down a 1 (for the 6 itself) and a 0 for each digit following it, and we get 10000, which is the place value, ten thousand:
3164297 | v 10000 --> 10,000's place
Using powers, our number can be expanded this way: $$31\underline{6}4297 = 3\cdot 10^6 +1\cdot 10^5 +\underline{6\cdot 10^4} +4\cdot 10^3 +2\cdot 10^2 +9\cdot 10^1 +7\cdot 10^0$$
Here’s a question from 1997 asking the same question in reverse:
Place Value - Units Digit
Notes on terminology: What is place value?
I want to add one more answer here, from 2003, that was not put in the archive for publication:
I am a sixth grade mathematics teacher. My wonderful college professor/mentor told me that there is no such thing as place value, and that books/teachers are using this term in error. He taught that a number has its place and its value, but that the term place value is incorrect. Yet, every book I find talks about it as place value, but I see his thinking and understand. I even think I agree, but I cannot find anyone or any book that explains this. What does your panel say about this?
I replied, sort of agreeing:
I wouldn't say there is no such thing, but I'm not comfortable with the way teachers are taught to use the phrase. Perhaps my thoughts are similar to yours, if I understand you correctly. In my mind, "place value" is a concept, not a number: the idea [also called "positional notation"] of writing numbers so that the contribution of each digit to the number's value depends on its place. Of course the term _is_ commonly used in a more concrete sense, as the actual value of the place; and I see no reason to deny the existence of such a thing. What bothers me is that it is so hard to express all the relevant "values" in a way that is not confusing to children (or at least to me). For example, the other day I answered a question from someone who was using these terms, which seem to be common: face value: the value of the digit, e.g. 7 (for the 7 in 8765) place value: the value of the place itself, e.g. 100 (hundreds) value: the value of the digit in its place, e.g. 700 (7 hundreds) I've seen various permutations of these words and others to cover the three values, but none seem to be really standard, and all can be easily mixed up. Why should the "place value" of a digit not be the value of the digit in that place, 700, rather than the value of the place itself? Why should the "value" of the digit not be the value of the digit itself? The worst usage is when people say (and this is a quote from one of the pages I found on a quick search) "the largest digit each place value can have is a nine", confusing "place value" with "place".
If the three terms listed there were standard, I could live with that. But even in talking to that other student, I struggled a bit with the fact that the “face value” of money is the number on the bill, which is not 7 but 700! Any terms you use are arbitrary, and therefore not really meaningful without general agreement.
I myself prefer to use descriptive phrases rather than brief names: the value of the digit itself, the value (or meaning) of the place, and the value of the digit in its place, or the value the digit contributes to the number. (By the way, did you use the word "number" to mean "digit"? That's another of my pet peeves...) The trouble, of course, is that nobody bothers to talk about these things except educators, and they assume what they are saying (from whatever book they use) is correct. If "correct" just means what is used most often, then in that sense they are right; but that doesn't mean it's the best terminology they could use. I suspect many mathematicians might feel as I do, but the issue is below their radar, since we have no occasion to discuss it.
I have generally had the sense that math educators are far less careful about definitions, and about general agreement, than mathematicians! And it’s in that sense (as a term used by mathematicians in particular) that the “place value” of a digit does not exist.

Pingback: Place Value: Decimals – The Math Doctors
Pingback: How Roman Numerals Work – The Math Doctors