Last time we looked at the concept of place value as children first learn it, with whole numbers. Here, we’ll expand that to look at decimals.
What do we mean by decimal?
First, we need to deal with what the word means, because it is used ambiguously. Here is a question from 2004:
Defining Decimal Numbers Can you tell me examples of decimals? Is 6.5 a decimal? Is 3.141592.....a decimal? I'm getting confused because I know that 6.5 has a whole number in it, so is it also a decimal?
The specific question seems to be whether anything with a decimal point in it is a decimal, but it called for a little more. I answered:
The word "decimal" is actually a very tricky one, and I'm not quite sure that there is a correct answer to your question! The word is used so loosely that most uses of it are really wrong. If you're confused, it's because the world is confused. Properly speaking, since the "deci-" in the word means "ten", ANY number written in a base-ten system (that is, with each digit worth ten times as much as the one next to it) can be called a "decimal number". When we write "123", the 3 is worth 3 ones, the 2 is worth 2 tens, and the 1 is worth a ten of tens, or a hundred. That is decimal.
So the “decimal number system” is our base-ten positional system in general. The emphasis of the word itself is on the base. A decimal numeral is one written using base ten.
But we also talk about "decimal fractions", which are non-whole numbers written in that way, using a decimal point. The trouble comes when people shorten that to "decimals", dropping the part of the phrase that really says what they want to say (that it is not a whole number) and keeping the part that is true of any number we write today. A decimal fraction, also called a decimal, is a number with a decimal point in it, like 1.23.
So a “decimal” in this sense is a non-whole number written in decimal form, which requires a decimal point. (“Fraction” is also used in different ways; here I am not requiring it to be less than one, as we sometimes do.)
Then people talk about the "decimal part" of a number, which really means the FRACTIONAL part, the non-whole part. This is even worse, making it sound like the 1 in 1.23 is not decimal while the .23 is. The reality is that both parts are "decimal", but only the .23 is fractional. But the common usage can make us think that 1.23 is not a decimal, but a mixed number, like 1 23/100, and that only numbers less than 1, like .23, can be called decimals. The point that divides the two parts, of course, is called a "decimal point", when what it marks is not really the start of the decimal part, but of the fractional part. I wish we called it something else, like "fraction point". But of course, a fraction is written like 23/100, so that would be confusing too.
This addresses Michael’s main issue. The number 6.5 is a decimal, though we call .5 specifically its decimal part. It’s much better to call it the fractional part, but we tend to think of “fraction” as referring to a number written as a fraction, like \(\frac{1}{2}\).
If you have heard about writing numbers in bases other than ten, such as base 5, we can get really confused when we want to talk about fractional numbers written in the place value system. Are they "base 5 decimals", when "decimal" means "base ten"? I don't think so! But we don't really have a good word for it.
This is why using decimals to refer to non-whole numbers is a pet peeve: It makes it impossible to talk about the corresponding concept in non-decimal bases. In other bases, we call the point the “radix point”, and the part after it the “fractional part”. But that just extends the error, as “radix” means “base”! “Fractional separator” is better.
I hope this hasn't just confused you more. I just want to show why you may get different answers to your question. In my opinion, any number with a decimal point in it would be commonly called a decimal, not just a number less than 1.
Since I am not an authority on word usage (either in math or in daily life), I didn’t stop there:
When I answer a question about words, I like to check with a dictionary, to see if the lexicographers, who define words for a living, and constantly watch how words are really used, agree with my impression. Here is what Merriam-Webster (m-w.com) says: Main Entry: decimal Function: noun :any real number expressed in base 10; especially: DECIMAL FRACTION Main Entry: decimal fraction Function: noun :a fraction (as .25 = 25/100 or .025 = 25/1000) or mixed number (as 3.025 = 3 25/1000) in which the denominator is a power of 10 usually expressed by use of the decimal point I think they agree exactly with me: a "decimal" is any number in base 10, but is usually used specifically for a number with a decimal point. So the answer to your examples is "yes".
That’s a relief.
Decimal places for children
Like last time, we can get started on the concept itself with a letter from a mother in 2003:
Why the Decimal Point Goes Where It Does I am trying to help my daughter understand decimal place value. Could you help me with a chart for her to study with? I'm having trouble getting her to understand that the first place before a decimal is "ones", and the first number after the decimal is "tenths". I've been trying to explain it using money. I'm using dollars as resemblance to whole numbers and change as resemblance to fraction.
Doctor Ian answered:
I'm somewhat hesitant to provide a chart. The thing about charts is that you either understand enough to make one yourself, or you don't. In the latter case, it means that the most you can do with the chart is try to memorize what's on it, and that's usually a bad idea. Money can be good, but for this to make sense, she needs to understand the basic idea of how decimal notation works.
Ask Dr. Math does provide a place value chart, here.
But since the goal is understanding, he presents the idea of place value as he did last time for whole numbers:
Let's look at a number like
123.45
We can write this as a sum:
100
20
3
.4
+ .05
--------
123.45
Does this make sense? When we see it broken up like this, we can see that each digit tells us how many groups of a certain size we have. In this case, we have
1 group of 100
2 groups of 10
3 groups of 1
4 groups of .1
5 groups of .01
Now we need to think about what those group sizes mean.
First, let's look at the groups to the left of the decimal point. Each one of them is a power of 10, that is, 10 raised to an exponent:
1000 = 10^3 10*10*10 = 1000
100 = 10^2 10*10 = 100
10 = 10^1
1 = 10^0
The last one is a little weird, but it's important to know about it, or the rest of the system doesn't really make sense.
So when we write a number like 3047, that's the same as
3047 = 3*1000 + 0*100 + 4*10 + 7*1
= 3*10^3 + 0*10^2 + 4*10^1 + 7*10^0
Note that we have to have the zero in there (between the 3 and the 4). Do you see why?
This is “expanded exponential form”, which we touched on last time. The zero represents an “empty” group of hundreds, and is needed as a “filler”, so that the other digits have the right place value.
So in this way, we cover all the group sizes where the exponent is zero or larger. What about when it's less than zero? Before reading any further, you should probably take a look at this: Properties of Exponents http://mathforum.org/library/drmath/view/57293.html Ready to go on? We can have negative powers of 10, as well as positive ones: 1000 = 10^3 10*10*10 = 1000 100 = 10^2 10*10 = 100 10 = 10^1 1 = 10^0 .1 = 10^-1 1/10^1 = 1/10 .01 = 10^-2 1/10^2 = 1/100 .001 = 10^-3 1/10^3 = 1/1000
Negative powers of ten represent fractions whose denominators are positive powers of ten. (Each time we decrease the exponent by 1, we divide by 10.)
So as you can see, we're using _all_ the powers of 10. The only question remaining is: Where should we put the decimal point?
...
In the end, we want numbers like
* = 1
** = 2
*** = 3
and so on to be as simple as possible to write, since they're the ones we write most often. Of all the places where we might put the decimal point, between 10^0 and 10^-1 is the one that causes the least trouble.
The goal is to separate the whole part from the fraction part.
So if you want to figure out the value corresponding to a place, here's how to do it without a chart. Suppose we have a number like
3175634.442586
What role is the 7 playing? Let's write out just that part of the sum,
3175634.442586
70000
and let's write the group size by changing the 7 to 1:
3175634.442586
70000
10000
How big is this? Adding commas can help:
3,175,634.442586
70,000
10,000 <-- ten thousand
That’s how we handled whole numbers last time. The decimal places are a little harder:
What about the 8? Let's start the same way:
3175634.442586
.00008
.00001
Now we can count up the exponents:
3175634.442586
.00008
.00001
|||||
1||||
2|||
3||
4|
5 So the group size is 1/10^5,
or 1/100,000 (1 with 5 zeros)
I know this seems like a lot to take in, but believe me, it's worth understanding, rather than trying to memorize a chart.
Note that you count all the way to the end, and that gives you the number of zeros in the denominator. You don’t just count the zeros.
Is there a “oneths” place?
Continuing a thought from that answer, we’d previously had this fun question from 1998:
The Oneths Place Why is there not a oneths place? My classmates and I were wondering. It is weird that decimals begin with tenths, hundredths, and so on. We appreciate your help.
This is a favorite of mine, because from time to time we’d get questions about “oneths” (at least a couple dozen), and I was able to point out that the question was not so unusual – if they searched our archives for that non-word, they’d find it!
I replied:
Hi, Cag. This is a good question. It could be answered by just saying "There isn't one, so accept it!", but it deserves some more thought. Let's think about it a moment: What are "oneths"? A "oneth" would be 1/1, so there already is a "oneths" place. It's called the ones' place. You don't need another. As I'll explain in a moment, this is a lot like the reason there is no -0: negative zero is the same as positive zero, so we only need one of them in the number line.
So the “ones place” would just be another name for the “ones place”, or “units place”.
What you're noticing is that the place values don't seem symmetrical, or balanced. On the left we have 1, 10, 100, and so on. On the right we have 1/10, 1/100, and so on. Shouldn't everything on the right match up with something on the left, 1/10 with 10 and so on? Or to put it another way, when we convert, say, 1/1000 to decimals, we find that although 1000 has three zeroes, 0.001 has only two! Why can't it be simpler? Place values really are symmetrical. The problem is that the center is at the ones' place, not at the decimal point where we would like it to be. If you think of the ones as being in the middle, then as you move to the left, you multiply by 10 each time, and as you move to the right, you divide by 10 each time.
We tend to expect places to match up this way, but they don’t:
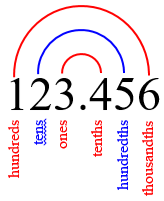
The symmetry instead looks like this:
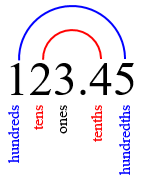
The ones stand alone.
The trouble is caused by the decimal point: it's off-center. It was natural to put it to the right of the ones' place, to separate the fraction part of a number from the integer part, but that takes away the symmetry. What you have to do is to think of the ones' digit as special, and count places to the left or right of that. For example, 1000 has two zeroes to the left of the ones', and 0.001 has two zeroes to the right of the ones'. The 1 in 1000 is three places to the left of the ones' place, and the 1 in 0.001 is three places to the right of the ones' place. If we wrote numbers by underlining the ones' place rather than putting a decimal point after it, there would be no confusion.
In fact, something like that underline idea has been used! One early attempt at writing decimals (Joost Bürgi) put the marker not to the right of the units place, but above (or under) it, so that what we write as \(14.3\) would look like \(1\overset{\circ}{4}3\). The little zero marked the zeroth power, as we’ll see in a moment. Others put numbers over decimal places, like \(14\overset{1}{3}\). And some used a vertical bar as a separator: \(14|3\). Any of these works; what we have chosen makes it easy to add a fractional part to a whole number.
Another way to look at this is to relate place values to the number line. Each place corresponds to a power of ten:
123.45
means this:
1 2 3 . 4 5
* * * * *
100 10 1 1/10 1/100
Each of these place values is 1 either multiplied or divided by some number of tens:
1*10*10 1*10 1 1/10 1/10/10
We can write this using an exponent. Positive exponents mean you multiply 1 by that many tens, and negative exponents mean you divide by that many tens:
10^2 10^1 10^0 10^-1 10^-2
Now look at the exponents: they form a number line, and the zero is not at the decimal point, but at the ones' place.
<-----+-------+-------+-------+-------+----->
2 1 0 -1 -2
In the number line we have not only positive and negative values, but also zero, which is neither positive nor negative but in between. It doesn't belong on either side, but in the middle. On the number line we can see it that way, but in a number the 10^0 place has to go on one side of the decimal point. There aren't both a positive and a negative zero, and there aren't both ones and oneths. The ones' place, just like 0 on the number line, belongs in the middle.
I hope that helps. It's interesting how we tend to expect things to be symmetrical. Mathematicians and scientists often expect it too, and when things don't seem balanced, they try to find out why. So keep wondering about things like this.
Curiosity made the mathematician!
Zeros at the end, I
There are several issues raised by zeros in decimal numbers. The next question, from 1998, is about the effect (or not) of zeros at the end of the number:
Ignoring Zeros Here's the problem. I just want to know what to do. You have 0.76 and 0.760 and you have to find out which number is greater or less, or if they are equal. My teacher says they are equal. The thing I do not understand is the number 0.760. Is point 760 thousandths right or wrong? So shouldn't 0.760 be greater? Or does the zero not count?
I answered:
Hi, Cole. This is an important question! Basically the answer is, as you suggested, that the zero doesn't count; but it's important to understand why that particular zero can be ignored, but others can't.
There are several ways to explain the meaning of a decimal. One is to treat it as one big fraction, so that:
76 760
0.76 = --- and 0.760 = ----
100 1000
Now look closely, and you'll see that you can simplify 760/1000 by dividing the numerator and denominator by 10 to get 76/100. Does that look familiar? I've just shown that these numbers are equal.
Here we are thinking of 0.76 as 76 times 0.01, that is, 76 hundredths; and 0.760 as 760 times 0.001, or 760 thousandths. Simplifying the latter, we find that they are the same fraction: $$\frac{760}{1000} = \frac{760\div 10}{1000\div 10} = \frac{76}{100}$$
Another way to look at decimals is by place value, just as you did for whole numbers. Then we can say that
1 1 1
0.760 = 7 * -- + 6 * --- + 0 * ----
10 100 1000
Now do you see that the zero doesn't add anything to the number? That's why it can be ignored. It's actually the same reason you can ignore the zero in 076, which just means no hundreds, just as this zero means no thousandths.
So a zero at either end, when there is a decimal point in the middle, can be ignored, because it adds nothing and doesn’t change place values when it is removed.
Now what about zeroes that aren't at the end? Look at the meaning of 0.706:
1 1 1
0.706 = 7 * -- + 0 * --- + 6 * ----
10 100 1000
That's not the same as 0.76, because now the 0 does something: it changes the meaning of the 6 from 6 hundredths (in 0.76) to 6 thousandths (in 0.706).
We call this zero a place-holder – it is necessary so that other digits have the right places.
So the rule is: when there is a zero at the left side of a number (to the left of the decimal point), or at the right side of a number (to the right of the decimal point), you can ignore it. If a zero is between two non-zero digits, or between a digit and the decimal point, you have to pay attention to it. I hope that helps.
Zeros at the end, II
Here is a similar question from 2001, but with mixed numbers:
Zeros after the Decimal Point I have a group of students that just can't comprehend my explanation of how 3.70 is equivalent to 3.7 or 3.700 or 3.7000... especially when you say 3.70 is 3 and 70 hundredths. Can you give me some insight into how you might go about the process of explaining the equivalent aspect of this concept? Thanks. P.S. I have noted that adding the extra zeros does not change the value.
I answered again, giving essentially the same explanation. At the end, I added this:
If you still face resistance, you might want to make it more concrete (say, ask whether they want you to give them three dollars and seventy cents, or three dollars and seven dimes). Or, ask them to convince you that the numbers are different, and then tell me what they said so I can see their reasoning.
We didn’t get a reply, unfortunately.
Next time I have one more discussion of zeros in a decimal.

Pingback: Should We Put Zero Before a Decimal Point? – The Math Doctors
Pingback: Decimals in Word Form: Basics – The Math Doctors