Distances to an Arc: Exact and Approximate Formulas

(A new question of the week)

It can be an interesting challenge to be presented with a formula and asked how it was derived. This becomes a bigger challenge when the formula is only approximate, so we have to figure out how to arrive at this particular approximation. But it is impressive when several different approaches all naturally lead to the same approximation! We’ll bring in geometry, algebra, trigonometry, and some results from calculus to attack this puzzle.

The question

This question came in last month, from Cvetača:

Hello,

I have an equation as shown in the picture. That equation is an approximation of the distance from a chord to an arc. My question is, how is that equation derived? I have no idea how to explain it.

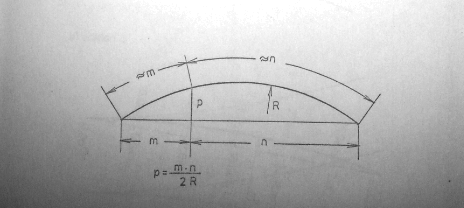
Here we have a chord of a circle, divided into two parts, m and n; the only other thing we know is the radius R of the circle. We want to find a formula for the perpendicular distance to the arc.

An exact formula would be considerably more complicated than the formula shown, \(\displaystyle p \approx \frac{mn}{2R}\). Where did this simple formula come from? And can we derive an exact formula for comparison? Finally, what is the significance of the markings for the two arcs in the picture? Do they suggest a particular derivation?

Geometry

After pondering the form of the formula, I saw one way to obtain it, by a favorite geometry theorem:

I’d be interested to know where it came from, and what was said about it. But I have a guess.

The formula implies that mn = 2Rp. This is reminiscent of the intersecting chord theorem, which says that mn = pq, where q would be the distance on segment p extended downward, until it intersects the circle.

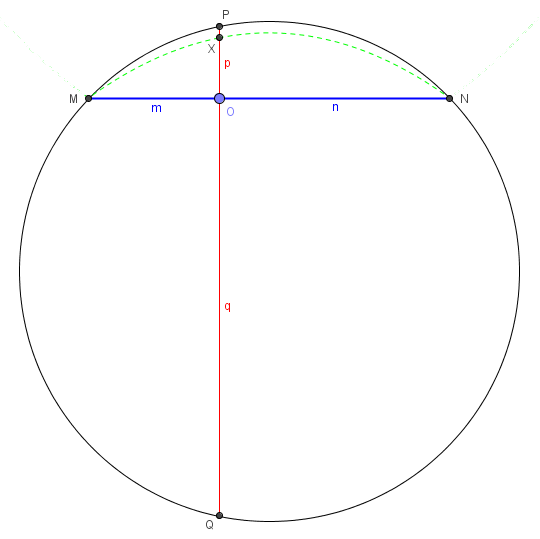
Therefore, the approximation assumes that q is nearly the diameter of the circle, i.e. the arc is small compared to the circle. In the image, I have shown the locus of the point X located by your formula, showing that it is close to the actual arc, but always smaller; if I move chord MN lower, it becomes considerably farther from the arc, but if I move it upward, the approximation improves considerably.

Now, the approximation may well have been derived differently, but this seems to be a particularly simple way to explain it. Others of us may well have additional ideas.

So one way to derive the formula is to assume that the arc is a sufficiently small part of the circle that we can ignore the difference between my q and the diameter. This might have been motivated by the theorem I referred to. But most approximations arise by other means.

Though Cvetača had no further comment, and no other Math Doctors made suggestions, I remained curious, and have subsequently played with the problem more, discovering several interesting approaches.

Algebra, version 1

First, let’s try applying the Pythagorean Theorem to the problem, solving for p algebraically and making an approximation by ignoring small terms at some point.

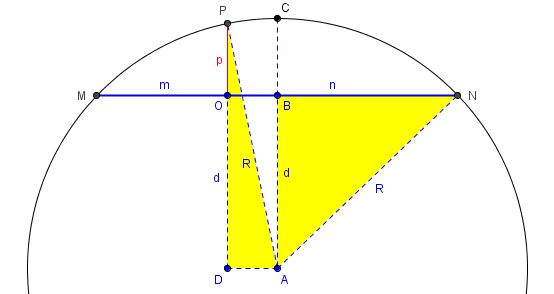
Since \(BN=\frac{m+n}{2}\) (half of the chord), triangle ABN yields the equation $$ \left(\frac{m+n}{2}\right)^2 + d^2 = R^2$$ where d is the distance of the chord from the center of the circle.

Since \(AD=\frac{n-m}{2}\) (the distance from the midpoint of the chord to O), triangle ADP yields the equation $$ \left(\frac{n-m}{2}\right)^2 + \left(d+p\right)^2 = R^2.$$

Expanding and subtracting the second from the first yields $$ mn – 2dp – p^2 = 0.$$

Assuming p is small (so that its square is negligible) and d is nearly R, we get, approximately, $$ mn – 2Rp = 0,$$ from which we obtain our goal, $$p=\frac{mn}{2R}$$.

Algebra, version 2

But can we solve to get an exact formula, and then simplify that? Yes, since we can express d in terms of m, n, and R. First, let’s solve that quadratic equation for p. We have $$ p^2 + 2dp – mn = 0,$$ so $$p = \frac{-2d\pm\sqrt{4d^2 + 4mn}}{2} = -d + \sqrt{d^2 + mn}.$$ But we have $$d^2 = R^2 – \left(\frac{m+n}{2}\right)^2,$$ and when we put that into our expression for p, with a little manipulation we get $$p = \sqrt{R^2 – \left(\frac{m-n}{2}\right)^2} – \sqrt{R^2 – \left(\frac{m+n}{2}\right)^2}.$$ That is our exact formula.

Now, there is a well-known approximation to the square root, which can be obtained from the extended binomial theorem, or from the power series, or from differential approximation: $$\sqrt{1 – x} \approx 1 – \frac{1}{2}x.$$ We can generalize this to $$\sqrt{a^2 – b^2} \approx a – \frac{b^2}{2a}.$$ Applying this, we get $$p \approx \left(R – \frac{(m-n)^2}{8R}\right) – \left(R – \frac{(m+n)^2}{8R}\right) = \frac{mn}{2R}.$$ There we are: a third derivation of the formula.

Trigonometry

As successful as we have been so far, we haven’t used the notations on the original picture showing the arc lengths as approximating the parts of the chord (which is not true in my picture, but would be for a sufficiently shallow arc). Surely they must be part of the original derivation. So let’s try focusing on those arcs and their corresponding angles.

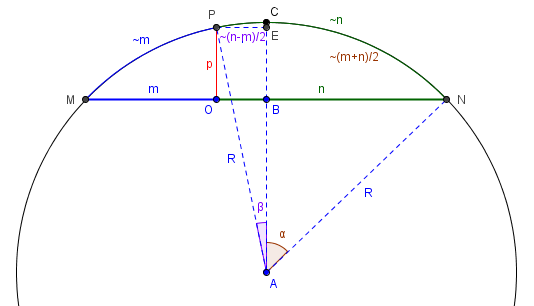
If we take arc MP as approximately m and arc PN as approximately n, then arc CN is \(\frac{m+n}{2}\), and arc PC is \(\frac{n-m}{2}\). The corresponding angles (in radians) are the arc lengths divided by R, namely \(\alpha = \frac{m+n}{2R}\) and \(\beta = \frac{n-m}{2R}\).

Now \(p = EB = AE – AB = R\cos\beta – R\cos\alpha\).

Again, we can use an approximation, \(\cos\theta \approx 1 – \frac{1}{2}\theta^2\). This gives us $$p = R\left(\cos\beta – \cos\alpha\right) = R\left(\left(1 – \frac{1}{2}\beta^2\right) – \left(1 – \frac{1}{2}\alpha^2\right)\right) = \frac{R}{2}\left(\alpha^2 – \beta^2\right).$$

Replacing the angles with their approximations, we get $$p = \frac{R}{2}\left(\alpha^2 – \beta^2\right) = \frac{R}{2}\left(\left(\frac{m+n}{2R}\right)^2 – \left(\frac{n-m}{2R}\right)^2\right) = \frac{mn}{2R}.$$

So now we have four ways to derive the formula. I imagine the last one, or something like it, is most likely the original.

A common question

We have received dozens of questions like the following, looking for the same result with different “givens”:

Formula for Laying Out an Arc

I work as a layout carpenter and do not have the advantage of the newer transits. I am working on a building having a 317' radius with steel centers along it, and will not be able to swing this radius with a measuring tape. If I could figure the layout from a chord it would be a great help. There must be a formula for this.

The radius is known, the distance from the center of the chord at 90 deg. to the arc is known, the distance from the center of the chord along the chord to a point is known - call it A. What would be the distance from A to the point where it intersects the arc at 90 deg. off the chord.            

Your help would be greatly appreciated.

The difference from the current question lies in what is known. Here, we know the radius r, the height h of the entire circular segment (from the chord to the middle of the arc), and the distance x from the center of the chord. The latter is closely related to our m and n, but above we didn’t know the height, which is what made it harder.

Here is a picture:

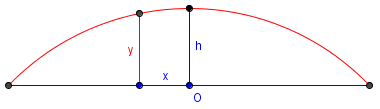
Doctor Rick answered this one:

I think I understand what you're saying, and it's not hard to work out using coordinate geometry. We can lay out our coordinate system so that the chord is along the x-axis with the center of the chord at the origin (0,0). If the radius is r and the perpendicular distance from the center of the chord to the arc is h, then the center of the circle is at (0, h-r), so the equation for the circle is

  x^2 + (y-(h-r))^2 = r^2

We can solve for y in terms of x:

  y = sqrt(r^2 - x^2) - r + h

This is what you're looking for: x is the distance along the chord from the center of the chord to your point A, and y is the perpendicular distance from point A to the arc.

Carl asked another question, and later told us he was regularly using this formula in his work.

Finding an unknown radius

Many others who have asked about the same calculation don’t know the radius, but only the height and the length of the chord. We have referred them to this page (or others like it):

Calculating the Radius from a Chord

If I know the chord length and chord height, is it possible to determine the radius of the circle? Is there a formula?

Here is my answer:

Hi, Katie. I assume that by "chord height" you mean the distance from the chord to the middle of the arc it cuts off. If so, there's a simple formula, and I'll even show you how to find it, if you can do a little algebra.

Here's my picture:

              *******
         *       |h      *
       *    d    |    d    *
      *----------+----------*
     *           |       /   *
    *         r-h|    /r      *
    *            | /          *
    *------------+------------*

I've called the length of the chord 2d, to simplify the calculations, so half the chord is d. The distance from the chord to the arc (your "chord height") is h, and the unknown radius of the circle is r. Then the distance from the center to the chord is (r-h). Incidentally, the technical term for h is the "sagitta" of the chord, and r-h is the "apothem." You don't hear those words used much. "Sagitta" is Latin for arrow. If you think of the arc as the bow and the chord as the string, you can see why.

Look at the right triangle with sides d, r-h, and r. Using the Pythagorean Theorem, we can say that:

    d^2 + (r-h)^2 = r^2         ("^2" means squared)

which expands to:

    d^2 + r^2 - 2rh + h^2 = r^2

and by subtracting r^2 from both sides we get:

    d^2 - 2rh + h^2 = 0

Now we can add 2rh to both sides:

    d^2 + h^2 = 2rh

and divide both sides by 2h to get:

        d^2 + h^2
    r = ---------
           2h

So the radius is just the sum of the squares of the height and half the length, divided by twice the height.

If you look back at the picture, d^2 + h^2 is just the square of the straight-line distance from one end of the chord to the middle. There's a simple geometric way to get the formula in that form, if you know enough about similar triangles.

Deriving our formula from these

In our case, though, we know the radius and the chord length, but not the height; we can solve this formula for h, which requires the quadratic formula:

$$r = \frac{d^2 + h^2}{2h}$$

$$2rh = d^2 + h^2$$

$$h^2 – 2rh + d^2 = 0$$

$$h = \frac{2r \pm \sqrt{4r^2 – 4d^2}}{2} = r \pm \sqrt{r^2 – d^2}$$

The two values this gives are for the major and minor arcs; we can choose the negative sign since we will only be interested in the minor arc.

If we put this expression for h into Doctor Rick’s formula for y, taking \(d = \frac{m+n}{2}\) and \(x = \frac{n-m}{2}\), we get $$p = \sqrt{R^2 – x^2} – R + h = \sqrt{R^2 – \left(\frac{n-m}{2}\right)^2} + \sqrt{R^2 – \left(\frac{m+n}{2}\right)^2},$$ which looks familiar from my work above. We’ve come full circle, so to speak.