This is part 2 of a series of extracts from discussions we have had on whether multiplication implied by juxtaposition is to be done before division (which I call IMF, for Implied Multiplication First). Some people write to us claiming that there is one official correct answer. Are they right?
Online calculators are misleading
Last October, Julia from Wisconsin had a simple version of the question:
I’m seeking assistance because I’m genuinely curious … as to who is right and who isn’t.
Okay so basically I was on Reddit today and a viral math problem appeared in r/YoungPeopleYouTube. It was quite literally written as 8÷2(2+2). Now me and a fellow redditor are at an impasse: they say the answer is verifiably 1, and I say it is verifiably 16.
When I plug in the equation into Mathway or Wolfram Alpha (as it is written, so literally typing it out in order and not changing how I type it or any extra key commands, etc), both services change it into this: (8)/(2(2+2)) where 2(2+2) is the whole bottom of the fraction. If we were to solve the equation this way, naturally it would equal 1. 2+2=4 (parentheses first), then 4*2 (because with fractions you take care of the denominator first if you have nothing on top to do, correct?) which equals 8, 8/8=1.
But how I am understanding the equation as it is written (which I fully understand is a poor example, but it is just a meme after all) is rather that it needs to be processed through (or thought through) our minds as if it was written like this: (8/2)*(2+2). To my understanding, you do the parentheses first (which would equal 4), then you do the division because it comes first in the problem (M or D, A or S, left to right), so that gets you 8/2=4, then you’re left with 4(4), which naturally gets you the result of 16.
Who is right here? And why? Are these calculators inputting it wrong simply due to machine error? Or am I wrong in my thinking? Any help would be greatly appreciated! Thanks!
Julia finds “strict PEMDAS” most natural, but sees that some websites seem to assume IMF. Or do they?
I answered:
Hi, Julia.
This problem, or others like it, have been viral literally for decades. We have discussed the issue in our blog here:
Order of Operations: Implicit Multiplication?
As explained there, both approaches to evaluating mixed division and multiplication are taught, in different places. Yours, which treats all multiplications alike, with the same precedence as division, is commonly taught in America. The other, which evaluates multiplication written without a symbol first, seems to be common in other places, and among actual users of math. I explain in the subsequent post why I half-heartedly support the latter; but my overall advice is never to write such an expression. (On the other hand, I am troubled by the idea that inserting the multiplication symbol where it was previously only implied would change the value of an expression; that’s why it’s only half-hearted!)
People who post such questions likely know it will cause arguments, and enjoy doing so. You should just ignore it. It’s like arguing over British vs American spelling, only worse.
If you believe in IMF, you have to be consistent enough to know reflexively not to rewrite \(8/2(2+2)\) as \(8/2\cdot(2+2)\), because that would change its meaning, according to IMF rules.
I then repeated her experiments with online calculators, with more subtle results.
When I type the expression into Google, it gives the answer as 16, rewriting it as (8/2)*(2+2), along with various explanations of the issue, not necessarily correct! And when I type it into Wolfram Alpha in “natural language” format using either the obelus, 8÷2(2+2) or the slash, 8/2(2+2), it gives 16, translating it as (8/2)(2+2); but if I enter it as 8/2(2+2) in “math input” format, it translates it as a fraction with only 8 in the numerator, and gives the answer 1. This appears to be due only to how the math input works (as it makes this change within the input field), and not necessarily how they interpret the symbols. Using the obelus in “math input”, it still gives 16.
“Natural language”, on the left, means that it reads questions typed in plain English or symbols; it then shows its interpretation, which here shows that they follow the “strict PEMDAS” rule, doing all multiplications and divisions from left to right.
In “math input” mode, they use what you type (or buttons you click) as formatting instructions. When you type a slash, it inserts a fraction bar (as if you had selected the fraction button), and stays in the denominator until you explicitly exit; this can’t be taken as their interpretation of the expression as originally written, so it does not indicate acceptance of the IMF rule. (There is no obelus button; when you type “÷”, it just enters that without making a fraction, and gives 16.)
I find similar results when I use Mathway. When I type in 8/2(2+2), it translates it into a fraction as I go, like “math input” mode, and gives me this:
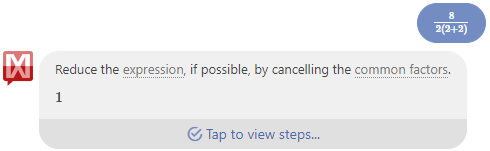
But when I paste in the same expression, 8/2(2+2), I get this, showing that it interprets the entire expression differently, using strict PEMDAS:
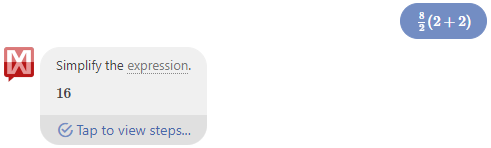
The same is true if I paste in 8÷2(2+2):
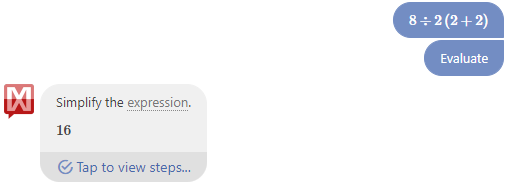
It would be harder to type that.
Conclusion: All these sites actually interpret expressions using strict PEMDAS!
But are they right?
Books that mention IMF
“Here’s where I learned IMF in the 1970s” … or not
Pete, from Georgia, wrote in early July, while I was writing this, and included an excerpt from his 1969 textbook, “Mathematics for Management and Finance with Basic and Modern Algebra”, 2nd ed. by Stephen P. Shao, Ph.D.:
I replied:
Thanks for the image from the book. I have long searched for examples of explicit teaching in a textbook, new or old, that specifies that implied multiplication is to be done first; this may be the first. Evidently this is American, despite the impression I have that it is American (high-school-level) texts that teach what I call “strict PEMDAS”.
(Actually, on reading more closely, it says that all multiplications are done before divisions, not just implied multiplications – though the latter are all they use. I’ve less often discussed this third option.)
This third option, All Multiplications First (AMF), is mentioned in the Historical Caveats post, where I refer to this explanation by Cajori:
I argued against it, however, in Order of Operations: Common Misunderstandings.
I would welcome examples of books, from anywhere and any time, that do explicitly teach about order of operations with implied multiplication, regardless of their view.
Common Core doesn’t mention IMF … but a book about it agrees with us
Allison (from Canada, whom we met last time) said this:
I have found older generations to do it the previous way and newer generations to do it the new way (seeing as all one question).
It is quite possible that strict PEMDAS is taught more often today, in Canada as in the U.S.; I simply don’t know.
I replied to this, in part:
I have from time to time tried to find evidence as to what rule has been taught when, and to the best of my knowledge, it has always been somewhat mixed, to the extent it has been taught at all. As far as I can recall, when I learned algebra in the 60’s, they just didn’t write things like 6/2(1+2). We have heard from students who were taught both ways in their textbooks, and some who used workbooks that followed a different rule in their answers than their textbooks or teachers. We have heard from parents who think that each approach is what they learned long ago.
I don’t think there is any “new math” vs “old math” on this topic. There is, instead, variation.
I would agree with your concern about “certain grades teaching it one way and then you end up in the upper grades with older teachers re-teaching it a different way”, if that is what is actually done; do you have evidence of that? It appears that you are in Canada, judging by your address; I don’t know their standards. The U.S. Common Core standards don’t state the order of operations rules, just saying that students should be taught to follow them! I found this Dummies page (claiming to represent Common Core) that appears to teach the implied-multiplication-first rule while calling it an “unspoken subtlety”, but concludes as I do that it should be avoided:
Maybe these people got it right. There is really no way to know what the person who wrote the expression meant for it to say, and that brings you back to where you started.
In any case, the solution is simply to teach students not to write ambiguous expressions, rather than to ask what is the “right” way.
The Common Core standard 6.EE.2.c, for example, merely says,
Evaluate expressions at specific values of their variables. Include expressions that arise from formulas used in real-world problems. Perform arithmetic operations, including those involving whole-number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations). For example, use the formulas /(V=s^3/) and /(A=6s^2/) to find the volume and surface area of a cube with sides of length /(s = 1/2/)
The “Dummies” reference, an excerpt from the book Common Core Math For Parents For Dummies, was one I had just found in searching for what Common Core might say. Here are more quotes from it:
But PEMDAS misses some subtleties. Among these subtleties are the following rules, which are often unspoken:
- Do implied multiplications before division or explicit multiplication. Implied multiplication refers to something such as the 2(12) seen in the above expression, where there is no multiplication symbol. …
The order of operations is an agreement among people that eases communication. If someone writes an ambiguous expression, such as
\(48\div2(9+3)\),then shame on that person for writing an ambiguous expression. If that person meant
\((48\div2)(9+3)\),then that’s what he should have written. If he meant
\(\displaystyle\frac{48}{2(9+3)}\),then he should have written that. The order of operations doesn’t exist to trick people with ambiguous mathematical expressions; it exists so that people can communicate their ideas more effectively.
Amen.
Claims of a universal standard
“Wikipedia says IMF is standard” … or not
David, from Australia, wrote this May; at one point he referred to several sources others have mentioned as supporting IMF:
I am not a mathematician, however I have completed a couple of years of university maths as part of my IT degree. However I had never heard of PEMDAS or BODMAS until long after I completed university degree.
I haven’t been able to find a serious article describing PEMDAS. My reference for the order of Operations is the Wikipedia page: https://en.wikipedia.org/wiki/Order_of_operations.
The paragraph that is relevant to this discussion is:
“In some of the academic literature, multiplication denoted by juxtaposition (also known as implied multiplication) is interpreted as having higher precedence than division, so that 1 ÷ 2n equals 1 ÷ (2n), not (1 ÷ 2)n. For example, the manuscript submission instructions for the Physical Review journals state that multiplication is of higher precedence than division, and this is also the convention observed in prominent physics textbooks such as the ‘Course of Theoretical Physics by Landau and Lifshitz’ and the ‘Feynman Lectures on Physics.”
So, if prominent academic sources state that implied multiplication is of higher precedence than division I think it is reasonable to describe this as a rule.
I have to say PEMDAS wasn’t part of my early learning, either. And it’s true that mathematicians don’t talk about it.
The sources quoted in Wikipedia are essentially all that I have found; a similar set were mentioned in a comment on my original post, and had been by others before that, as well as in videos. (It’s curious that they are mostly from physicists rather than mathematicians!) It’s also interesting that the rule these references support is not IMF, but all multiplications first, which is definitely not what is typically taught in textbooks today.
He omitted this statement in Wikipedia:
This ambiguity is often exploited in internet memes such as “8÷2(2+2)“, for which there are two conflicting interpretations: 8÷[2(2+2)] = 1 and [8÷2](2+2) = 16.
They recognize an ambiguity, rather than declaring that there is just one answer. (Of course, we need to recognize that Wikipedia is not just one person, and can contradict itself; but perhaps that is the point.)
He continued:
My questions for you are:
- Why does PEMDAS get an answer that disagrees with the accepted order of operations used by mathematicians.
- Are you seriously suggesting that order of operations is a choice where I can choose the international standard and get the answer 1 and others can use PEMDAS and get 36?
I replied, in part:
I don’t expect to convince either the American educational establishment, or the calculator manufacturers, to drop the rigid interpretation of “PEMDAS”. So all I can do is to emphasize the ambiguity surrounding this, and especially tell people to avoid those silly memes that are intended to get people arguing.
Let’s answer your two explicit questions.
To the first: It’s because, obviously, people have come to at least three different “consensuses” about this. Basic P(E)(MD)(AS) is one of those; all multiplication before division [P(E)MD(AS)] is another; implied multiplication before others [P(E)J(MD)(AS)] is a third. These are different choices that can be made, and have been made, as Wikipedia points out.
To the second: Yes, of course it’s a choice. That’s what a consensus is: A choice that many people agree on. We need consensus in order to communicate; Any language is a consensus, in which other choices could have been made. I’m not advocating individual, chaotic choice! But we don’t have a universal consensus. This is not a good thing, so we need to talk about it. We can’t just pretend that everyone agrees, and ignore those who don’t.
There is no absolute “international standard”. I don’t like it either, but the references here do not prove that there is, and I have found nothing better.
“ISO standards resolve the question” … or not
David also said this:
Many calculators give different answers depending on whether you use the solidus (/) or obelus. The symbols are interchangeable. Therefore the answers should be the same. The relevant ISO standard says the obelus should not be used.
This last point is one that I have seen increasingly; unfortunately the ISO [International Organization for Standardization] standard is not available to the non-paying public, so it can’t really be considered a public standard; and that means I have struggled to find out whether it actually provides the absolute standards people think it does. This led me to do some more research.
I responded to several points, including what we saw above about Wolfram Alpha (noting that he must be referring to online calculators), and closing with this:
Mention of ISO is interesting. In principle, you’d think that ought to be the final authority I’ve wished for – but it is not really written for mathematicians, and my impression is that mathematicians don’t pay much attention to it (see here on Stack Exchange, for example, particularly the answer by Zeping Lee). The fact that it is hidden behind a paywall takes away a lot of the authority it might have had, since ordinary people can’t actually use it. I haven’t read it, but have occasionally found snippets of it, and this one (Section 7.1.3 of ISO 80000-1:2009) is interesting for our discussion:
“These procedures can be extended to cases where the numerator or denominator or both are themselves products or quotients. In such a combination, a solidus (/) shall not be followed by a multiplication sign or a division sign on the same line unless parentheses are inserted to avoid any ambiguity.”
In other words, they agree with me that the main solution is to never write such an expression. They do not solve it by decreeing what is the proper order of operations; I don’t get the impression that they actually state a complete order of operations as we might wish they would. (I believe their reason for deprecating the obelus is primarily that it has different meanings in different countries.)
I have since found more excerpts from ISO 80000-1 and -2; the following appears to be all that is relevant to the order of operations:
ISO 80000-1:
ISO 80000-2:
What I see here is that they are trying to avoid any ambiguity, even recommending that you add a space in \(ab^{-1}\), which is unambiguous as written, and around binary operators except the solidus for clarity. They ban the obelus, “÷”, because it is sometimes used for subtraction or negation, and recommend avoiding the solidus, “/”, because it looks too much like the letters “I” and “l“. They don’t like \(a/b/c\) or \(a/b\cdot c\), which could be misread by mistake, and don’t even mention \(a/bc\)! The focus is not on how to interpret an expression, but how not to write it – which is our point.
(When they mention “altering the order of operations”, they don’t mean changing the rules, but rewriting “\(\ln x+y\)” as “\(y+\ln x\)”.)
They do say that multiplication and division have precedence over addition and subtraction, but not that either multiplication, or implied multiplication, has precedence over division.
I concluded:
So that’s where I leave it. Since there are different opinions in reputable sources, and no one authoritative source, the best I can do is to point out the ambiguity and recommend avoidance, which is what I’ve been doing for 25 years.
The only people who insist on writing such expressions, in my experience, are Internet trolls who want to start arguments. I choose not to join them, nor to agree with people who predict catastrophe if this isn’t fully resolved. This simply isn’t that important.
Pingback: Implied Multiplication 3: You Can’t Prove It – The Math Doctors
Hello, Doctor Peterson,
Since you’ve revisited the topic of implicit multiplication in order of operations, I write to share some observations. Before addressing specific topics, let me say that I agree with your overall conclusions:
Expressions like “8÷2(2+2)” are de facto ambiguous, so it’s best not to write such expressions, at least if your goal is to communicate ideas clearly and not simply to start an argument. And if you come across such an ambiguous expression in your reading, you ought to be careful about interpreting it. (Unfortunately, well-meaning authors do sometimes write such ambiguous expressions, perhaps because they imagine that they are following a generally accepted convention, or perhaps because they simply don’t notice the potential ambiguity at the time, and thus follow what I might call the “I knew what it meant when I wrote it” convention.)
Moving on to specific topics, …
* * * * * * * *
Common Core:
You wrote: “The U.S. Common Core standards don’t state the order of operations rules, just saying that students should be taught to follow them!” I noticed the same thing and share your bemusement. The link you supplied for the standard isn’t working for me, but I found these alternative links:
https://www.nctm.org/uploadedFiles/Standards_and_Positions/Common_Core_State_Standards/Math_Standards.pdf
https://learning.ccsso.org/wp-content/uploads/2022/11/Math_Standards1.pdf
On page 36, I find these parenthetical remarks about addition and multiplication of fractions:
Page 42 has this about division of fractions:
In all three cases, the intended interpretation for the expression to the right of the “=” sign is implicit multiplication first (IMF). On page 77, however, I find the expression “1/2 ab sin(C)” for the area of a triangle, clearly intended with the strict PEMDAS interpretation (1/2) ab sin(C).
* * * * * * * *
ISO Standards:
You have quoted, from some ISO document, an admonition that “…, a solidus (/) shall not be followed by a multiplication sign or a division sign on the same line unless parentheses are inserted to avoid any ambiguity.” Note the words “multiplication SIGN” (my emphasis). Arguably, the passage you quoted doesn’t say anything one way or the other about multiplication indicated without a sign—that is, implicit multiplication.
While many ISO documents are expensive, ISO does offer a free SI summary brochure, linked from this page:
https://www.bipm.org/en/publications/si-brochure
Looking at the English language portion of the current (9th) edition of the brochure, I find on page 132 the expressions “1/μ₀c²” and “1/μ₀c”, meaning 1/(μ₀c²) and 1/(μ₀c), respectively (IMF interpretation). On page 204, I find “(2π⁵k⁴/15c²h³) T⁴”, meaning (2π⁵k⁴/(15c²h³)) T⁴” (also IMF).
Do the expressions I just cited confirm my speculation that the phrase “… shall not be followed by a multiplication sign …” was never meant to forbid implicit multiplication following a solidus? Or was the intent really to forbid all expressions whose meaning might depend on the precedence of multiplication (whether explicit or implied) vs. division, and was someone connected with ISO not following their own rules when they wrote the expressions I just cited? Also, if I were to look at a lot of ISO documents, would I find that they sometimes include expressions meant to follow strict PEMDAS rather than IMF, similarly to the expression “1/2 ab sin(C)” that I found in the Common Core standard? I wouldn’t be surprised if the answer to that last question were Yes, but I’m not about to spend hundreds of dollars on ISO standards documents in order to find out.
* * * * * * * *
Online Calculators:
Here are some examples of behavior of online calculators to add to the ones you mentioned.
1) While Wolfram Alpha (in “Natural Language” mode) interprets the input “1/2x” as (1/2)x, it interprets “1/xy” as 1/(xy). The input “1/xy, where x = 2, y = 3” thus gives the result 1/6 (displayed with a horizontal fraction bar). I learned about this from comments by Jenni Gorham in discussions about PEMDAS on her “The How and Why of Mathematics” YouTube channel.
2) As far as I know, the Google calculator doesn’t recognize input expressions containing variables, such as “1/2x”. It does, however, recognize some symbolic constants. In particular, although it interprets “1/2(3)” as (1/2)*3, giving the result 1.5, it interprets “1/2pi” as 1/(2*pi), producing the approximate value 0.15915494309. You can also give it the input “1/2π” (getting the “π” symbol by using a keyboard shortcut or by copying the symbol from someplace and pasting it) with a similar result. Similarly, it interprets “1/2e” as 1/(2*e), giving the result 0.18393972058.
I could share a variety of other examples of the behaviors of calculator apps, symbolic algebra systems, and programming languages, but I’ll stop here.
* * * * * * * *
You also asked about “books, from anywhere and any time, that do explicitly teach about order of operations with implied multiplication, regardless of their view.” I have found several examples, but I will save them for another message.
Hi, Jim. Thanks for the additions (and also for information you have provided in the past, which I didn’t include in the new posts for the sake of space — but may in the future).
What you have done with regard to both Common Core and ISO is what I didn’t have the patience to do: looking beyond what they explicitly teach to examples of what they actually do. (By the way, I did include one of the links you provide for Common Core, in addition to the broken link to a specific spot … which I left in because it looked like it may be a temporary issue. It’s probably good to make it more visible.)
Examples, of course, are tricky, because we can’t know whether any inconsistencies are intentional, or the result of the same sort of oversight that, to me, makes these expressions inherently ambiguous regardless of rules. The use of 1/2 in “1/2 ab sin(C)” is one I frequently point out; I suspect that there is an unstated rule that a space after a fraction acts like parentheses, just because it looks like it should. A descriptive (not prescriptive) grammar of algebra might well mention that! And I suspect that it is this sort of behavior that leads to claims that scientists and mathematicians in practice follow IMF, and also the reason many students do: It just feels natural, whether you’re taught it or not.
By the way, it has long interested me that in writing compound units, like “meter per second”, the official rule is to use negative exponents rather than division (as in “m -1s” rather than “m/s”). I’ve wondered if that was an attempt to avoid these very ambiguities. But I see that used right alongside the examples you found of expressions with division. (And I notice now that section 5.2 of the brochure does allow the solidus, but also requires either an explicit dot or a space for multiplication.)
The information on calculators is also interesting. Ultimately, of course, that isn’t really relevant to what the “official rules” might be, as any programming language can set its own rules, which may depend as much on the needs of their medium or accidents of programming as much as on whether or not they try to follow standards.
Hello Dr. Peterson,
The expression of “x divided by x” is one monomial divided by another monomial. Since anything divided by itself (given that “x” is not zero), the quotient is 1. In 5th grade, young math students learn that Fraction=Division & Division=Fraction. This is reiterated & demonstrated in Basic Algebra, just a few years later. For example:
from Teaching Better Lesson .com Common Core:
https://teaching.betterlesson.com/browse/common_core/standard/272/ccss-math-content-5-nf-b-3-interpret-a-fraction-as-division-of-the-numerator-by-the-denominator-a-b-a-b-solve-word-problems-invo?from=standard_level1
“Interpret a fraction as division of the numerator by the denominator (a/b = a ÷ b).”
~ ~ ~ ~ ~ ~ ~
Australian Association of Mathematics Teachers:
https://topdrawer.aamt.edu.au/Fractions/Big-ideas/Fractions-as-division
“Fractions as Division”
“Anyone who has studied secondary school mathematics would probably be comfortable with the convention of ‘a over b’ meaning ‘a divided by b’.”
~ ~ ~ ~ ~ ~ ~
from Algebra Class .com: https://www.algebra-class.com/dividing-monomials.html
“Dividing Monomials”
“Remember: A division bar and fraction bar are synonymous!”
~ ~ ~ ~ ~ ~ ~
from Study .com FAQ’s:
https://study.com/learn/lesson/monomial-examples-factors.html
“Monomials are the product of a coefficient, and a variable or variables.”
~ ~ ~ ~ ~ ~ ~
from BrainFuse .com:
https://www.brainfuse.com/curriculumupload//1339003048076.html#:~:text=Whenever%20a%20term%20appears%20without,is%20the%20same%20as%20%2D1x.&text=Like%20terms%20(or%20similar%20terms,variables%20with%20the%20same%20exponents
“Whenever a term appears without a numerical coefficient, we assume that the coefficient is 1. For example, x is the same as 1x”
~ ~ ~ ~ ~ ~ ~
And some examples…
Lumen Learning Courses:
https://courses.lumenlearning.com/uvu-introductoryalgebra/chapter/9-5-dividing-polynomials-by-a-monomial/
“Dividing Polynomials by a Monomial”
EXAMPLE
Find the quotient: 56x^5 ÷ 7x^2
Solution
Rewrite as a fraction
56x^5
______
7x^2
.Answer
56x^5 ÷ 7x^2 = 8x^3 ”
~ ~ ~ ~ ~
from Mathway:
https://www.mathway.com/popular-problems/Algebra/1012959
“Enter a Problem”
” 2x ÷ 2x
Rewrite the division as a fraction
2x
___
2x
… 1 ”
~ ~ ~ ~ ~ ~
Open Stax. org
Elementary Algebra
https://openstax.org/books/elementary-algebra-2e/pages/6-5-divide-monomials
“Divide Monomials”
“Example 6.72
Find the quotient: 56x^7 ÷ 8x^3 ”
Solution
Rewrite as a fraction:
56x^7
_______
8x^3
~ ~ ~ ~ ~ ~ ~
I used Wolfram Alpha’s online calculator “NATURAL LANGUAGE” input.
When I use the input of…
Divide 1x by 1x
https://www.wolframalpha.com/input?i=divide+1x+by+1x
…the answer is shown as the top-and-bottom fraction
1x
___
1x
…which equals 1.
But when I input it as “1x divided by 1x,” the answer is shown to be x squared.
https://www.wolframalpha.com/input?i=1x+divided+by+1x
Those two statements (“Divide 1x by 1x” & “1x divided by 1x”) are the exact same thing. Therefore they should come out to the same quotient. Hence, there is a logical inconsistency in Wolfram Alpha’s computer program for monomial division.
In the case of stating the expression as “Divide 1x by 1x,” the Wolfram Alpha online calculator correctly displays the top-and-bottom fraction of 1x over 1x, in accordance with 5th grade math’s lesson of Division=Fraction, and when there is a one term divided by another single term.
In the other case, stated as “1x divided by 1x,” the Wolfram Alpha calculator has been programmed to interpret the expression with the order of operations as PEMDAS (or GEMDAS, going strictly left to right). That is demonstrably WRONG. Since 5th graders are taught that Division=Fraction, then the fraction of one monomial (a single term which is the PRODUCT of the coefficient multiplied by the variable) being divided by another monomial should be 1x over 1x. The way to simplify a fraction (i.e. a division expression) is to perform all of the operations indicated in the numerator (dividend), then do all of the operations indicated in the denominator (divisor), and finally, divide the numerator by the denominator. Therefore, given that x does not equal zero, 1x divided by 1x equals 1.– no matter which division notation is used (since Division=Fraction & Fraction=Division).
I have never seen any Basic Algebra textbook which instructs students NOT to treat a monomial such as 1x as ONE TERM with a SINGLE VALUE (i.e. as a PRODUCT) & instead young math students are specifically instructed to treat 1x as two completely separate entities (i.e. as “1” and “x”), so they should “peel off” the coefficient & use it in another operation in the mathematical expression BEFORE doing the implied multiplication. If you can find a Basic Algebra textbook that demonstrates that exact method for dividing one monomial by another monomial by “peeling off” the coefficient, I’d love to see it!
Hi, Dee.
The first part of this contributes nothing to the discussion; we all know that a fraction is a division, but that says nothing about notation, since we have to decide what is the numerator/dividend and what is that denominator/divisor in order to interpret an expression. Nor is your emphasis on the word “monomial” helpful; I touched on that here.
When you show examples in Lumen and OpenStax, we already know that there are (many) books that write division of monomials this way (I’ve already shown some), but it’s worth noting that both sources do this just once, and thereafter use the safer notation with the horizontal bar.
I discussed Mathway in this post, so that’s nothing new.
You’ve added a little to the discussion of Wolfram Alpha, by entering expressions in words; but that, too, is irrelevant, because the order of operations applies to symbolic expressions; in Natural Language Mode, they just do the best they can to figure out what someone is saying, and don’t always get it right. I do think it’s bizarre that they take “1x divided by 1x” differently than “divide 1x by 1x”. I would interpret both as (1x)/(1x); but I would write it this way, with parenthesis, if for some reason I didn’t write \(\frac{1x}{1x}\), to make sure a reader didn’t take it wrong. In any case, we already know that Wolfram Alpha is inconsistent even when working with fully symbolic expressions, from what I said above. Complain to them, not to me! But it is the existence of bizarre interpretations that forces me to urge people to write defensively.
As for your last paragraph, I agree! I don’t think I’ve ever seen a textbook that explicitly applies PEMDAS in this situation; I’ve repeatedly asked for someone to show me such a textbook. (See here, for one, and elsewhere in these comments.)
All I know is that enough students have either been taught the rigid PEMDAS idea by their teachers, or have applied in contrary to what they were taught, that we got questions about it long before memes existed.
Hello Sir Dave, I also agree that this is somewhat ambiguous case. But still, people will still argue and continue to contradict each other. I am firmly in favor of giving higher priority to Implicit Multiplication or Juxtaposition. As that is what I’ve been Taught and learned about thru further research, some of which were shared to me by a friend and some I got from YouTube.
SECOND COURSE IN ALGEBRA by: Prof Herbert Hawkes, PhD – COLUMBIA UNIVERSITY
pg. 1 chap.1 (1926)
PRE-ALGEBRA (An Accelerated Course) 1996 and MATHEMATICS – New Edition (Structure and Method) by Mary P. Dolciani, Robert Sorgenfrey. John Grahan
p. 6 (1992)
ALGEBRA 1 by Houghton Mifflin Compony
-Variables may be a grouped in the same way that numerals are grouped. When you group a product that involves a variable, you usually omit the grouping symbol (Implied grouping).
e.g. (5n) + 2 = 50 + 2
16 ÷ (4y) = 16 ÷ 4y
(8a) – (5b) = 8a – 5b
ALGEBRA (Structure and Method) by Mary P. Dolciani, Richard Brown & William Cole
-Note that yz ÷ 10n = (yz) ÷(10n)
MODERN ALGEBRA by Mary P. Dolciani and William Wooton
Similarly ab ÷ 7n = (a*b) ÷ (7*n)
THE NEW ALGEBRA by H.E. Slaught, PH.D. SC.D. and NJ Lennes PH.D. pg.101
(1926)
INTERMEDIATE ALGBERA By Ron Larson and Robert Hostetler – 2008
pg.17 The order of operations for multiplication applies when multiplication is written with the symbol x or *. When multiplication is implied by parentheses, it has higher priority than the left-to-right rule.
For instance: 8 ÷4(2) = 8 ÷ 8=1
But 8 ÷ 4 *2 = 2*2 = 4
What are Quantities? Intro to Algebra Bonnycastle
pg 13: a and b are factors of ab ; 3abc is a composite quantity.
pg 25: simple quanities; examples on pg 26 such as 6ab÷2a=3b
https://books.google.ca/books/about/Bonnycastle_s_Introduction_to_Algebra.html?id=1YhTAAAAYAAJ&redir_esc=y
(1844)
Basic Algebra I, Second Edition Nathan Jacobson
https://books.google.ca/books?id=JHFpv0tKiBAC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
pg 116: a/b + c/d = (ad +bc)/bd
Introduction to Algebra Peter Jephson Cameron
https://books.google.ca/books?id=syYYl-NVM5IC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q=mx&f=false
Page 17
Online sources:
http://www.onlinemathlearning.com/multiply-divide-expressions.html
http://www.purplemath.com/modules/orderops3.htm (Elizabeth Stapel: http://www.purplemath.com/resume.htm)
Discussion on algebra: http://www.jstor.org/stable/pdf/2972726.pdf
and again, Every Education Approved Scientific Calculators used Juxtaposition, Giving higher priority to implicit or implied multiplication over Explicit Multiplication.
It appears that the universal accepted consensus is that to give higher priority to Juxtaposition. The PEMDAS thing is just an oversimplification of the Order of Operations and therefore is in complete can’t be trusted to solve equations or operations not belonging the acronym PEMDAS. PEMDAS was created for Elementary school children for them to have the basic understanding of the Order of Operations and ready them to higher mathematics.
Hi, Jojo.
Thanks for the list of books; I have taken the time to find actual images, which I’ll include here, from some of them in place of your (sometimes inaccurate) quotations from them (which I deleted). The books I am most interested in are those that explicitly teach about how to handle implied multiplication; as I’ve said before, when IMF is simply used, it is not entirely clear whether it is intentional, though it does suggest it. I’ve removed a few of your references that I didn’t find helpful for this reason.
Initially I was pleased that you agreed with me; but such a long list suggests that you are involved in the online wars that I prefer to avoid. As I said in part 1, this just isn’t that important.
I have a couple specific comments about some of your examples.
Some (Hawkes, Slaught and Lennes) are from around Cajori’s time, which makes it particularly interesting that they explicitly teach this; in fact, in looking for the books online, I found various editions and got the impression that those published before the infamous Lennes Letter don’t seem to mention it, but those afterward do. But also, the Slaught and Lennes book doesn’t teach IMF, but AMF (All Multiplication First – on page 102, which I include here although you didn’t mention it), so it doesn’t entirely fit in a list supporting IMF.
Hawke: “it is customary to think of the indicated multiplication as already having been performed”
Slaught/Lennes: “this is the universal practice”
Page 102: “all multiplications are performed first”
Bonnycastle is of historical interest, going back as far as 1844; I think your comments about “composite” and “simple” quantities reflect a misunderstanding, because the relevant contrast is between “simple” and “compound” quantities, the latter involving sums. I don’t see that ab being composite (a product) plays a role in his treating it as a unit – but it’s true that he does.
The Dolciani books are familiar to us; I recall 20 years ago someone writing to us about them, which was our first exposure to the fact that IMF is actually taught. Doctor Ian mentioned it several times (not archived), and it helped to soften my comments at the time. It all depends on what we have been exposed to.
I was particularly interested in the quote from Larson and Hostetler, and wish I were able to find an image of it to confirm how much of what you quote is what they actually say.
The book I’m most interested in would be one that explicitly teaches strict PEMDAS applied to implied multiplication; it may well not exist, and it may be only hyper-literal students or teachers who apply it that way and cause all the fuss.
Most of the other books in your list, some of which I have deleted as a waste of space, are just examples of actual usage, which we already know exist. There is no need to make huge lists of them.
At the end, unfortunately, you deviated from your initial claim and made some absolute declarations. When you say, “Every Education Approved Scientific Calculators used Juxtaposition, Giving higher priority to implicit or implied multiplication over Explicit Multiplication”, that doesn’t follow from the evidence you give, and in fact is outright wrong. The standard school calculator (TI-30X IIS) sitting in front of me says that 8/2(2+2) = 16, which I understand to be because American educators convinced TI to use the rule that they taught, rather than what earlier calculators did. If I were not in America, I would likely be firmly on the side of IMF (but still recommending avoidance of even potentially ambiguous expressions).
I agree that PEMDAS is just an inadequate summary, and that it is a mistake to overapply it; it probably does not represent, when taken literally, the usual practice either whenever it was invented, or now.
Let me repeat yet again what I have said before in various ways: I am happy to follow IMF, and even to recommend it as more natural, and perhaps more common; I just insist that (a) it is a choice, even if almost universal, and not something you could prove to be the only acceptable rule; (b) it is not universally taught; and (c) people who make a big issue of it are wasting their time. Those are the points of the three posts in this series, in reverse order.
This is the reference on Implied Multiplication by Larson and Hostetler.
Study Tip
The order of operations for multiplication applies when multiplication is written with the symbol x or •, When multiplication is implied by parentheses, it has a higher priority than the Left-to-Right Rule. For instance,
8 ÷ 4(2) = 8 ÷ 8 = 1
But
8 ÷ 4 • 2 = 2 • 2 = 4
Order of Operations
One of your goals in studying this book is to learn to communicate about algebra by reading and writing information about numbers. One way to help avoid confusion when communicating algebraic ideas is to establish an order of operations. This is done by giving priorities to different operations. First priority is given to exponents, second priority is given to multiplication and division, and third priority is given to addition and subtraction. To distinguish between operations with the same priority, use the Left-to-Right Rule.
Order of Operations
To evaluate an expression involving more than one operation, use the following order.
1. First do operations that occur within symbols of grouping.
2. Then evaluate powers.
3. Then do multiplications and divisions from left to right.
4. Finally, do additions and subtractions from left to right.
—————
The study tip is on the left side of the page in the “Intermediate Algebra” 4th edition (1981) Order of Operations page.
There is an almost identical page but modernized coloured version in the 2008 “Intermediate Algebra” section 1.2 page 17. Same left side of the Order of Operations page.
I would send the exact page but can’t seem to send a photo image for you here.
Thank you for your time.
Thanks, Andrew.
I’ve tried searching for this page; Archive.com has several editions or variations of the book, but none contain this comment. From Google Books, I was able to cobble together this image:
It’s curious that this is just a sidebar, and contradicts/overrides the list of rules in the main text; but that seems to be the role that this concept has always played: not an official “rule”, but an exception that is followed by those in the know. You’d think it would also be found in similar contexts in other books by the same (nominal) author.
But at least this fills in a gap, confirming that the idea has been formally taught, and that the quotation above was accurate.
(If you’d like to send an image, you can use our Ask a Question site, where attachments are permitted.)
So, is the answer in your example 1 or 4? We’re having a debate on that very thing at the moment.
As I said at the end of the post above, “The only people who insist on writing such expressions, in my experience, are Internet trolls who want to start arguments. I choose not to join them, nor to agree with people who predict catastrophe if this isn’t fully resolved. This simply isn’t that important.”
Andrew showed one book that explicitly teaches that 8 ÷ 4(2) = 1; but not everyone follows that rule.
Just stop debating.
If we take the expression 8/2(2+2) as an example we know that following PEMDAS gives 16 and following IMF gives us 1.
Step 1. So let’s start with a slightly different expression: 4/(2+2),
Both PEMDAS and IMF evaluate this to 1.
Step 2. Then multiply the numerator and denominator by 2. This does not change the value which must still be 1.
The expression can now be written as:
8/2(2+2) the expression we were originally asked to evaluate, and this must still equal 1.
Step 3. As I have shown that the expression must equal 1 we must assume that the PEMDAS process for calculating this expression is incorrect and the IMF process is the correct one.
Happy to get your thoughts on this proof.
Hi, David.
This would fit better in the next post, Implied Multiplication 3: You Can’t Prove It, where we discuss similar attempts to prove one interpretation “correct”.
Some of the arguments there are similar to yours, though yours is perhaps a little more subtle; and they have the same basic answer. As I say there about substitutions, “You must always think about meaning before you rewrite an expression, rather than deriving meaning from an unthinking rewrite.”
Here’s the problem: When you “multiply the numerator and denominator by 2”, you are identifying the numerator as 4 and the denominator as (2+2); but in then writing “8/2(2+2)”, you are implicitly (no pun intended) assuming that 2(2+2) is still the denominator. You could just as easily have written “2*4/2*(2+2)”, which clearly (unless you believe in All Multiplications First) does not mean what you intend it to mean.
When you want to multiply numerator and denominator by 2, and want to be sure you actually do that, you need to parenthesize to avoid risk: “(2*4)/(2*(2+2))” or “(2(4))/(2(2+2))”. In the next post, I call this “preemptive parentheses”.
Or, better yet, write it as \(\frac{4}{2+2}=\frac{2(4)}{2(2+2)}\), which makes it clear what is the denominator. Generally speaking, I recommend avoiding any horizontal form when manipulating anything; the horizontal forms are only for compact writing in print.
I am making more of a statement than a question.
PEMDAS is not an all inclusive Anagram, it does not include everything. PEMDAS does not tell you where other Mathematical expressions get processed.
If P is Parentheses inside only then E must also be Exponents only. So where do Fractions, Factorials, and other Implied Functions get processed.. by Strict PEMDAS there is no letters for calculating those Functions. (Fractions are Implied Addition [ex: 1½= 1+½= 1/1+1/2= 2/2+1/2= 3/2 which is the proof that “a b/c= (c×a+b)/c”], Factorials and Juxtaposition are Implied Multiplication [3!=1×2×3, and 3(2)=3×2 or more accurately 3!=(1×2×3), and 3(2)=(2×3) .. and that shows the expressed groupings of Implied Mathematical Functions.)
In reality Strict PEMDAS does not consider Fractions and higher level math expressions. PEMDAS says Left to Right only.
If we consider 10÷3×6. Under Strict PEMDAS you have: 10÷3= 3.33, 3.33×6= 19.99.. however due to the Commutative Rule we can rewrite the expression to 6÷3×10= 2×10= 20 or use invert and multiply 10×⅓×6= 6×⅓×10. It is only by violation of Strict PEMDAS-Left to Right that we can achieve the correct answer of 20.
I had a professor that said “When doing PEMDAS, Remember PIX .. Parentheses/Implied/eXpressed ..after Parentheses comes Implied followed by eXpressed”.
A few clarifications may be in order.
Much of what you say summarizes what I’ve said in more detail in these posts. About the acronym PEMDAS being an incomplete expression of the rules, see Order of Operations: The Basics. In particular, about fractions and factorials, see Order of Operations: Fractions, Evaluating, and Simplifying and Order of Operations: Neglected Details, respectively. And the fact that in mixed numbers (not fractions in general) juxtaposition means addition is part of the reason we tend to avoid them in algebraic contexts. I use “implied” or “implicit” to refer to operations indicated without any symbol at all (that is, by juxtaposition), so factorial is an explicit operation (indicated by “!”). But you are right to use what I have called “preemptive parentheses” when expanding them.
When I use the (made-up) term “strict PEMDAS”, I am referring to the assumption that all multiplications, explicit or implicit, are to be treated alike; any (proper) understanding of PEMDAS assumes that (at least explicit) multiplication and division are done from left to right. Your example of 10÷3×6 has no implicit multiplication, so the term is irrelevant there. I don’t understand your comment about “violation of Strict PEMDAS-Left to Right”
Good afternoon,
The expression in question is 100/5(2)+10. A couple of different PEMDAS calculators provided two different solutions. There’s nothing to act on within the parenthesis, but does the 5 in front imply multiplication before moving on to the rest of the expression? That’s how I treated it and came up with 20 as the solution for the expression. Some came up with 50. What’s your evaluation?
I think it should be clear from this page (e.g. the last two paragraphs of the post), as well as others like Order of Operations: Implicit Multiplication?, that both answers are common, and I consider such an expression ambiguous. I tend, currently, toward your answer if I had to choose; but I strongly prefer not to write expressions that way. No matter what I might think, there will always be people who would read it differently, so why take chances?
Multiplicación implícita quiere decir que hay que evaluar la expresión como si hubiera un signo de multiplicar delante del paréntesis. No lo hay, pero está implícito. En ese sentido la multiplicación implícita es una multiplicación y sujeta, por lo tanto, al orden izquierda a derecha.
Hi, Claudio.
Google translates your comment as
Evidently, you have been taught that implicit multiplication is treated the same as explicit multiplication, so that you follow what I have called “strict PEMDAS”. It is helpful to know that this idea is not restricted to the United States!