(Archive Question of the Week)
Fractions are a frequent source of questions from elementary students. I plan to devote several posts to various aspects of this, from using a common denominator to add fractions, to flipping and multiplying to divide fractions, to converting between improper fractions and mixed numbers. Here, I want to look at one answer to a teacher that covers several aspects of how fractions are related to decimals.
Why do you divide the numerator by the denominator?
Here is the question, from teacher Erin in 2001:
Dividing Fractions to find Decimals I have some students who do not understand dividing the numerator into the denominator to find out the decimal. I cannot give them a reason why you do this except that it works. Why does this operation work to give you the decimal form of a fraction?
First, let’s check out what Erin is asking about. To convert the fraction 3/4 to a decimal, students are taught to divide 3 by 4, which gives the answer 0.75. Or, to convert 8/9 to a decimal, they divide 8 by 9 and get the answer 0.888… , a non-terminating, repeating decimal, in contrast to the terminating decimal in the first example. Why do we do this? Knowing why can help the students remember what to do; it can also help them see that math makes sense, rather than being a list of rules a teacher tells you.
Since students often get the terminology wrong here, I had to start by pointing out that Erin didn’t quite say what she meant:
Let's be careful with our terminology, first: you mean dividing the numerator BY the denominator! A lot of kids get that wrong.
We sometimes describe “6 divided by 2″ as “how many times does 2 go into 6″, and then as “divide 2 into 6″, but this can then easily get turned around into “6 divided into 2″, which is not correct. I discussed this and related issues here:
Wording Division Problems
A fraction is a division
I continued into the heart of the matter:
The basic reason is that division is really what fractions are all about. In a very real sense, we can say that a fraction is simply a division we haven't bothered to perform yet, a division problem frozen in time. We write "3/4" to mean "I want to divide 3 by 4, but I don't want to do the work just yet, so I can simplify the work before I finish up." That's why we use the virgule "/" or the horizontal fraction bar to signify division in more advanced math (and in computer programming languages), rather than the old-fashioned obelus.
That is, where in elementary arithmetic we write division as \(10 \div 5\), using the symbol called an obelus, mathematicians more commonly use the horizontal bar, \(\frac{10}{5}\) or the virgule or slash, 10/5. These show that we think of division as being the same thing as a fraction.
But why?
Let's go back to the basics of fractions to see why I can say this. What are fractions? The essence of a fraction is a division, a breaking into pieces. Take a whole object and divide it into 5 (equal) pieces; each piece is 1/5. We've divided 1 by 5, just as we divide 10 by 5 by dividing a set of 10 things into 5 parts, each of which consists of 2 objects. So 1 divided by 5 is 1/5; and 10 divided by 5 is the fraction 10/5, which simplifies to 2. Likewise, we can divide 2 pies into 5 parts by dividing each pie into 5 parts (fifths) and taking 2 of them at a time: 2 divided by 5 is 2/5. The denominator represents the number of parts we divide each whole into (a divisor); the numerator represents a multiplier, the number of parts we have. Let me repeat that, because it's easy to miss: 2/5 MEANS 2 divided by 5. The fraction IS a division.
Let’s do that in pictures:
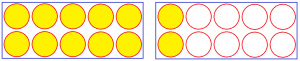

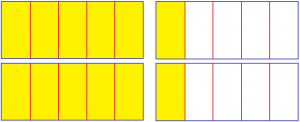
(I used rectangular “cakes” instead of round “pies”, to make the comparison easier.)
So, 1 divided by 5 means dividing 1 into 5 equal parts and taking 1 of them; the result is the fraction 1/5. And 2 divided by 5 means dividing 2 into 5 equal parts, each of which is 2/5. In each case, the fraction is what you get when you divide.
At a higher level, moving away from pictures of cakes or pies, we define division as the inverse of multiplication — that is, working backward to find the missing factor that will give a known product. For example, we say that \(10 \div 5 = 2\) because 2 is the number you can multiply by 5 to get 10: \(10 = 5 \times 2\). This is how we check a division: Do the multiplication and see if you get the right number back. So we can check my claim that \(2 \div 5 = \frac{2}{5}\) by multiplying: Is it true that \(2 = 5 \times \frac{2}{5}\)? Yes, it is.
One more little perspective on it:
Now look at the operations on fractions. When we multiply by a fraction, we're really dividing: 1/2 * 10 is half of ten, or ten divided by 2, or 10/2 again. Fractions mean division.
Half of something means dividing by 2; and in general, multiplying by a fraction “1 over something” means dividing by that “something”.
To convert, we just do what it says
Now, if a fraction is a division, what does that imply?
So when we want to convert a fraction to an ordinary (decimal) number, all we're really doing is waking up a division problem that has been in suspended animation, and letting it continue: "Where was I? Oh, yeah ... 3 divided by 4 ... that's 0.75."
In other words, if we want to get 3/4 in a different form, namely a decimal, we just do the division the fraction represents, in terms of decimals.
For more on converting fractions to decimals (and more), see our FAQ:
Converting Fractions, Decimals, and Percents
This page demonstrates two ways to convert a fraction to a decimal (and also how to convert a simple decimal to a fraction):
Converting Fractions and Decimals
Also, this answer takes what I said above one step further, looking at why we use the fraction bar to represent division in algebra as well as arithmetic:
2a/5 or 2a Divided by 5?
Finally, here is a 2009 restatement of the ideas I presented above:
Why Does Division Convert a Fraction to a Decimal?
The last paragraph says it well:
Now, when we convert a fraction to a decimal, all we are doing is carrying out, in decimal form, the division that the fraction represents. That is, in my example, we've said that 3/4 means 3 divided by 4, so we go ahead and divide 3.00 by 4 and get 0.75. Since both 3/4 and 0.75 are obtained by dividing 3 by 4, they are two ways to express the same number!
