A recent question asked about an interesting locus, which led me to realize we haven’t talked about that topic in general. Here we’ll look at what a locus is, using three simple examples, and then dig into a question about the wording.
What it is
We’ll start with this question from 2003:
The Meaning of Locus What is the locus of points equidistant from two parallel lines 8 meters apart? I have trouble understanding the meaning of locus.
Since it was assumed in the answer, I’ll point out that “equidistant” means “the same distance from both lines”.
I answered:
Hi, Marina. The idea of locus is very simple, but a little subtle. You can almost leave the word out of many problems; this one asks you simply to describe all points that are equidistant from the two lines. The point of the word "locus" is merely that you are to think of all the points that fit that description as a single entity, which might be a curve or line or a set of discrete points.
We’ll look further into the origin of the concept at the end. You could consider it an old word for “set”; in Latin the word locus means “place”. Our problem, then, is simply “Describe the set consisting of all points equidistant from two parallel lines 8 meters apart?” or “Where are all the points equidistant from two parallel lines 8 meters apart?”
Here are our two parallel lines:
Now we can answer the question:
So picture it one point at a time. What sort of point is the same distance from both lines? Imagine a point somewhere; how do you measure the distance from each line? You draw a perpendicular from the point to each line, and their lengths are the two distances. Now, what does it mean if they are the same? You will find that the points you are looking for are exactly between the two lines.
Here is one such point:
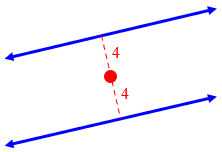
Once you get that idea, think about how you can describe all such points. Imagine that you were forced somehow to walk only in places that are the same distance from the two lines, perhaps because there is a rope from you to each of the lines and some mechanism keeps them the same length. Where will the grass be trampled down? That is the locus.
We’ll see this idea of trampled grass again later! Here is where all those points are (that is, the locus):
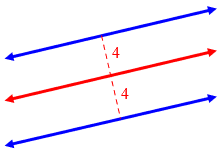
Notice that we can’t just think about some points that fit; we have to find them all, and to be sure no other points do. Once we see that, we need to describe what we see: the parallel line halfway between the two given lines.
Although the question doesn’t require it, we could prove that all points on this new line are equidistant from the given lines, and that every point equidistant from the two lines is on the new line. The first step, though, is to see it as we have done, so we can make a conjecture, and then prove that.
Perpendicular bisector as locus
For another example, consider this question from 1999:
Locus What do you have to do to get the perpendicular bisector of all the loci of a triangle? What does it mean when it asks you about equidistance from certain points?
The question this time is about the meaning of “equidistant”; but it’s not stated quite right, so we’ll have to rephrase the question as it was presumably given, explaining the terms that made it easy to misstate.
But one thing Jo got right: The plural of “locus” (which, as I said, is a Latin word), is “loci” (pronounced “low-sigh”, or, if you learned Latin as I did, “low-key”).
I answered:
Hi, Jo. Thanks for writing.
Your first question doesn't make a lot of sense, because there is no "locus of a triangle." But I think I can see what you're asking about.
A "locus" is the set of all points that satisfy some rule or description, and a perpendicular bisector is one of the simplest examples of a locus. If I asked you "what is the locus of all points equidistant from two given points?", the answer would be "the perpendicular bisector of the segment determined by the two points."
Here's what the question means:
What is the locus of all points ...
(What geometrical object consists of all points X ...)
that are equidistant from A and B?
(... for which the distances AX and BX are equal?)
That is, "equidistant from two points" means "the same distance from both points."
Here is a point that is equidistant from points A and B:
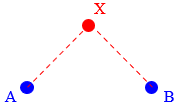
Here's what the answer means:
The perpendicular bisector ...
(the line through the midpoint of the segment,
perpendicular to the segment)
of the segment determined by A and B.
(you make the segment by connecting
A and B with a straight line)
That is, this line bisects segment AB (cuts it exactly in half) and is perpendicular to it (at right angles):
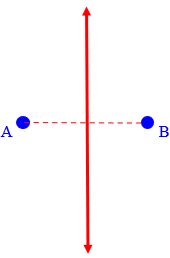
You can prove (and probably your text did this) that any point on the perpendicular bisector of a segment AB is the same distance from both endpoints; you can see this by drawing in the segments and seeing that you have an isosceles triangle, so that AX = BX:
|
+ X
/|\
/ | \
/ | \
/ | \
/ | \
/ | \
/ | \
/ | \
/ | \
/ | \
/ | \
/ | \
/ |_ \
/ | | \
+--------------+--------------+
A | B
|
|
This tells us that any point on the perpendicular bisector is equidistant from A and B, so it is part of the locus we are looking for.
This is only half of the requirement: Every point on the locus must meet the requirements, and also every point that meets the requirements must be part of the locus:
Conversely, you can show that if any point is equidistant from A and B, it must be on the perpendicular bisector, so there are no other points in the locus: the perpendicular bisector IS the entire locus we're looking for. That's what a locus is: the set of ALL points that fit some description (in this case, being equidistant from A and B). In our case, the perpendicular bisector is "the locus, the whole locus, and nothing but the locus" of equidistant points.
The word “all” is essential!
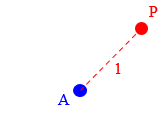
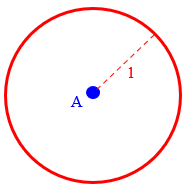
There are many other examples of a locus. For example, the locus of points 1 inch from point A is the circle of radius 1 centered at A. Every point of the circle is 1 inch from A, and every point one inch from A is part of the circle. I hope that helps a little to clarify the idea of a locus, and the meaning of equidistant. If you have problems you still have trouble with, maybe you can write back with a specific problem so I can see the wording of it.
Here is a point 1 unit away from point A:
Here is that circle:
We’ll see more examples next time.
Locus of “a point” or “points”?
I want to close for now with this question, from Navneet in 2016:
Locus Locution Which of these is the correct definition of a circle? 1. A circle is the locus of *a point* which moves in a plane in such a way that its distance from a given fixed point is always constant. OR 2. A circle is the locus of *points* which moves in a plane in such a way that its distance from a given fixed point is always constant.
Is one of these incorrect? Or are they both acceptable?
I answered, yet again (yes, this is a favorite topic of mine):
Hi, Navneet. The proper (older) terminology is "locus of a point." We define a constraint that applies to a point, and imagine following ONE POINT as it moves around subject to that constraint. We can also describe this as "the locus of all points that ...," thinking not of a single point moving, but just of the set of points satisfying the condition. This is the more modern usage that emerged with the development of the set concept. Your second version uses the idea of moving, which is not appropriate when talking about a set of points, so it is not good wording.
The first definition, “A circle is the locus of a point which moves in a plane in such a way that its distance from a given fixed point is always constant,” envisions the process of drawing a circle, in which a point, namely the point of a compass, is moving around, keeping a constant distance from the center. The locus is the circle it draws, which is the path it followed. We can call this the dynamic definition.
The second definition, which would have been better written as, “A circle is the locus of points in a plane in whose distance from a given fixed point is a given constant,” looks at the result of drawing the circle and sees that it consists of all points a given distance from the center. It doesn’t consider the motion, just the resulting figure. We can call this the static definition.
See this Wikipedia article, which explains the two usages (key phrases capitalized by me for emphasis):
https://en.wikipedia.org/wiki/Locus_(mathematics)
"Until the beginning of the 20th century, a geometrical shape (for example, a curve) was not considered as an infinite set of points; rather, it was considered as an entity on which a point may be located or on which it moves. Thus a circle in the Euclidean plane was defined as THE LOCUS OF A POINT that is at a given distance of a fixed point, the center of the circle. In modern mathematics, similar concepts are more frequently reformulated by describing shapes as sets; for instance, one says that the circle is THE SET OF POINTS that are at a given distance of the center."
The first perspective sees a locus as “where a point lives”, as a river is the “locus” of fish; the second, as the collection of such points themselves.
Thus, the common wording today appears in MathWorld:
http://mathworld.wolfram.com/Locus.html
"For example, THE LOCUS OF POINTS in the plane equidistant from a given point is a circle, and THE SET OF POINTS in three-space equidistant from a given point is a sphere."
You can see that the word “locus” can be replaced by the word “set”, as we see also here:
See also the Math Open Reference:
http://www.mathopenref.com/locus.html
"We can say "THE LOCUS OF ALL POINTS on a plane at distance R from a center point is a circle of radius R." In other words, we tend to use the word locus to mean the shape formed by a set of points. An odd thing is that you can often just drop the word locus, and it still makes sense: "The set of all coplanar points distance R from a central point forms a circle."
"... Sometimes the idea of locus has a slightly different explanation. If you think of a point moving along some path, we sometimes say that the path is the locus of the point. So for example a point that moves a fixed distance from another point draws out a circle. So we could say
"THE LOCUS OF A POINT moving at a fixed distance from a center point is a circle.
One problem is that a locus is not necessarily a path; it can be a plane in space, or a region such as the interior of a circle; these probably didn’t occur in the original uses of the concept.
Your reference books may well use the old form ("locus of a point") with or without explicit mention of motion. Other sources you find, especially online, are likely to use the new form ("locus of points") with no reference to motion at all.
Does that help?
More on the locus of a moving point
Navneet wasn’t quite sure about the “old form”:
What should be the appropriate and precise definition of the word "locus" in mathematics? We know that the definition of locus is "the *set of all points* (usually forming a curve or surface) satisfying some condition." But how can we use it for one point, as in "A circle is the locus of *a point* which...."?
I answered:
You aren't really asking about the DEFINITION, but about how the older WORDING fits that definition. I'll try to explain that in more detail. In the old wording, "the locus of a point MOVING under some condition" refers to the set of all places that that point will reach as it moves. Think of the point as a pen point moving around, and the locus as the ink mark it leaves behind. The pen is a MOVING point, not a single location; the locus (drawn curve) consists of all the points (fixed locations) where it ever traveled. In particular, a circle is the locus of the pencil point of a compass as it turns. I imagine that may be exactly what was in the mind of whoever first used the word "locus" in this way.
Again, the locus can be thought of as the path traced by the pen, or as the set of ink molecules on the paper. They both represent the same static entity.
Incidentally, we can describe a curve as a function of time (the path of a point), or we can eliminate time from the equation(s) and be left with just an equation in x and y (the equation of a curve). These are two views of the same locus. But the time factor is ignored in thinking about the locus.
Another example I've given is this: suppose you tether a dog to a ten-foot rope that you stake in the middle of your yard. What part of your yard will it trample? The dog can move around, but is constrained by the rope to stay within ten feet of the stake; so all the places that the dog could trample will lie in a ten-foot disk with that center. This is the "locus of the dog": the set of all points where the dog will ever travel. (A disk is the locus of points whose distance from the center is less than or equal to a radius.) Or, if the dog is like some I have seen, the actual part of the lawn it tramples may be not the interior of the circle, but the circle itself, since it will spend all its time at the end of its rope trying to get away. And in fact this is how we define the circle as a locus: the set of all points a fixed distance from the center. But we are describing it as the locus of "a point" (the dog) as it moves.
Long ago I had a neighbor whose dog behaved this way. Today, another neighbor sometimes attaches his dog to a “zip line”, producing a locus consisting of a pair of parallel lines if the dog is on a similar mood, or a rectangular region otherwise.
In the more modern wording, we don't think of a single point moving, but go directly to the idea of a set of points. Perhaps this change in common usage was made in part to prevent the confusion you are expressing due to the use of the word "point" in two different ways (moving and fixed). The meaning is the same whether we speak of many points or a single one.
Next time we’ll have more examples to illustrate these concepts, and will also move on to algebraic descriptions of loci.

Pingback: Finding a Locus: Algebra and Geometry – The Math Doctors