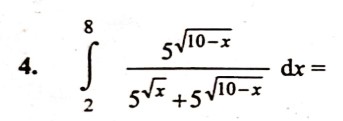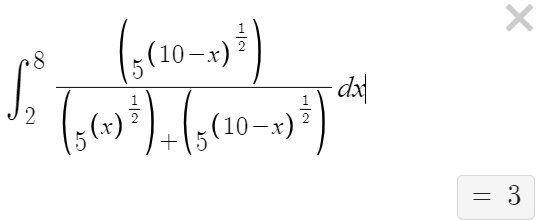(A new question of the week)
Definite integrals can sometimes be solved by finding an antiderivative; but when that is either difficult or impossible, there may be special tricks available. Here we’ll lead a student gradually to a solution using symmetry; and then we’ll look at an earlier problem that used essentially the same trick in a more elegant form.
Here is the question, from mid-April, from an anonymous student in India that I will call Swamy:
Could you please solve this question?
Reasoning to a strategy
I answered, starting with the usual disclaimer when someone asks for an answer without showing any work:
Hi.
We don’t just give complete answers, but we do give hints so you can solve problems yourself.
I’ll tell you my own chain of thoughts:
- First, I saw the repetition of similar radicals, and thought some substitution might make this easier to work with, perhaps one that would make the two different radicals more similar.
- Then I observed what the domain of the integrand is.
- Then I saw how the limits of integration relate to the domain, and saw that symmetry might be involved.
- At some point in here, I graphed the integrand on Desmos, and everything fit together, telling me what to do. I made the appropriate substitution, and could almost directly read the answer from the graph. (But the graph wasn’t essential to the solution.)
See what you can do with these ideas. It’s a nicer problem than I initially thought!
(If you can’t get closer to a solution, you can at least tell me what topics you are learning, and any ideas you think might be relevant, so I can improve my hint.)
I’ll fill in one detail now: The domain of the integrand is the intersection of the domains of \(\sqrt{x}\) and \(\sqrt{10-x}\), which is \([0,10]\). The limits of integration cover the interval \([2,8]\), which is centered in the domain. It is that centering that suggested symmetry.
Swamy replied:
I did try to do something with the substitution, but it kind of did not get me anywhere. I’ll try graphing as suggested. Thanks for the tip.
Negative information (“I didn’t get anywhere”) doesn’t help us help, so I asked for details:
Show me what substitution you are trying, and some of your work, and I can help more.
I’ll reiterate that a key is to look for a possible symmetry, and shifting the function so that its domain is centered on x=0 will help with that.
In other words, the specific substitution I had in mind was one that would, hopefully, make symmetry more visible. Swamy answered with work:
I’m sorry, I don’t understand how symmetry is involved in this case because the graph basically gives an asymptote. It’s kinda frustrating. T_T. I thought I was getting close but I ignored a term (accidentally) and realized about it in the end so, the whole thing was complete waste, but i got 3.78 and the actual answer is 3.
The last step of the work is wrong. But his substitution is similar to one that I might have tried, too, if I didn’t already have my idea about symmetry (namely, \(t=10-x\), without the radical – which we’ll see later as an alternative possibility). Unfortunately, what he did doesn’t simplify the problem at all. Note that my suggestion was a substitution that would make the two radicals more similar.
The second image shows that, rather than graphing in Desmos as I’d done, he used the site’s ability to evaluate definite integrals (numerically, I presume), which is not what I intended. I do sometimes use such features (usually in Wolfram Alpha) to check whether a problem has a solution, but it doesn’t help in actually solving (much less, of course, in learning how to think).
The role of symmetry
Now Doctor Rick stepped in:
Hi, I’m Doctor Rick and I’d like to make a few comments.
First, I’d like to know where this problem comes from. Is it a contest problem? It seems that way to me, because the suggestions Doctor Peterson has made are not the “standard” way we approach integration problems. Contest problems generally require “outside the box” thinking like this.
Some courses cover very specialized tricks for definite integrals; this one may or may not be explicitly taught in an introductory course. (The book used by students I tutor has a theorem about definite integrals of even and odd functions, which is the direction in which I was heading.) But many problems we get are from contests of various sorts where tricks are common (or just similar challenge problems from the Web, like last week’s question), and knowing whether they are related to a recently taught topic makes it easier for us to know what to expect of a student.
Second, you say that the graph “basically gives an asymptote,” but in fact it has no asymptote. If you consider the domain of the function, as Doctor Peterson suggested, you will see that the domain does not include ±∞, so the function can’t have a horizontal asymptote. Furthermore, it can’t have a vertical asymptote because the denominator cannot be zero.
Most likely that claim came from hasty consideration of the graph, as we’ll see momentarily. Asymptotes of some sort would cause trouble only if they made the integral improper.
Though you used graphing software to do the integration (so now we know what answer we want to obtain by some other means), you didn’t show the graph that the software produced. Perhaps you did make the graph, but misinterpreted what you saw.
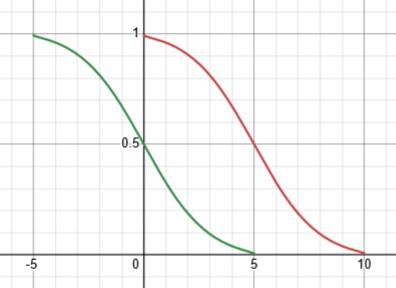
Here is the graph itself, showing how the limits of integration, \([2,8]\), are centered in the domain, \([0,10]\):
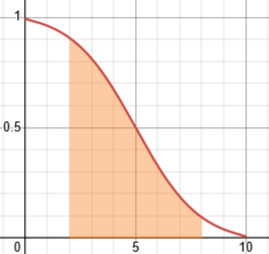
I can see how this could have been misinterpreted as showing asymptotes, if one did not first find the domain algebraically.
What we’re looking for primarily is symmetry. For instance, the graph of y = sin(x) is symmetric in the origin: If you reflected each point on the graph through the origin, you’d get another point on the graph. (This can also be described by saying that this is an “odd function”.) Similarly the graph of y = cos(x) is symmetric in the y axis: If you reflect a point on the graph across the y axis, you get another point on the graph. (This symmetry is also described by the term “even function.”)
A graph can be symmetric in a point other than the origin, or in a line other than the y axis. That’s something we’d like you to look for.
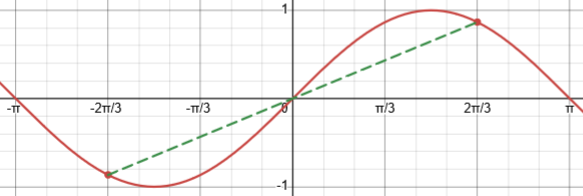
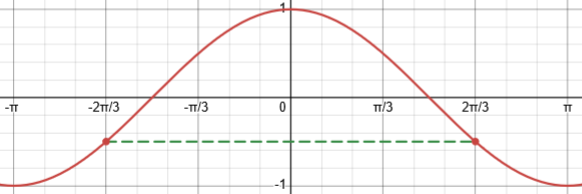
Here are parts of the graphs of sine and cosine, showing the symmetry of each.
The sine is an odd function, symmetric across the origin:
The cosine is an even function, symmetric across the y-axis:
These show how it is easier to see (and talk about) symmetry when the center lies on the y-axis; my goal was to lead him to see that, by transforming our function.
As a hint about how symmetry can help us, consider the integral of sin(x) from, say, -1 to 1. Can you see that the integral is zero without even doing the integration, just by considering symmetry? (Sketch the graph, and think of the definite integral in terms of areas above and below the x axis.) If this isn’t clear yet, it is worth discussing, because it’s a powerful concept.
Here is the region whose (signed) area would be calculated by the integral \(\int_{-1}^{1}\sin(x)dx\):
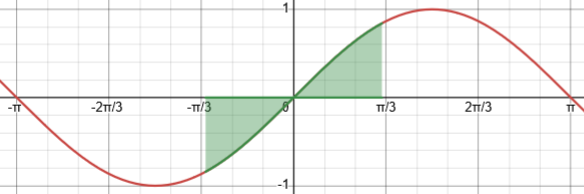
The left and right parts have the same area by symmetry, but with opposite signs, so they add to 0. This is true for any odd function integrated over a symmetrical region.
Stepping back
Swamy responded:
Thank you, Dr. Rick, for explaining the graph and grooming the topic for me.
Let me answer your questions:
- It’s not particularly a contest problem because the question appeared in an objective exam.
- I’m sorry, I was wrong by concluding the graph to have an asymptote.
Now, I do understand the concept of try to convert the integral graph into a symmetrical graph (I really do), but I am not able to do it. The concept is very clear to me, but could you please put this into application and discuss how we can solve the problem.
Unfortunately, saying you can’t do something, without showing your attempt, doesn’t help us to continue helping. I responded to two points.
On the source of the problem:
The reason we’re interested in the source is that we want’ to know how much to expect you to know, and in particular whether the problem is intended to test what you have been explicitly taught, or is intended to test your creativity beyond that (as contest problems do). If it is from a course exam, we’d like to know what that course is, and what topics relevant to definite integrals like this have been recently taught, so we can refer to that. In particular, were you taught about using symmetry for definite integrals? Can you show us an example problem that we might be able to relate to this one?
On showing work:
The more you tell us about your own thinking (what you can do, not what you can’t), the better we can help. For instance, if you show us your understanding of using symmetry by another example, that will help us see what to add to that.
The substitution you did, t = √(10 – x), is not the one I had in mind; my substitution will bring the center of the graph to the y-axis, making the symmetry easier to see. If you don’t see what that will be, please at least tell us what symmetry you see in the function, from the graph or otherwise, and also what the domain is, which as I indicated is a big hint.
Continuing with my graphs above, we can see that if we shifted the graph left by 5 units, both the domain and the limits of integration would become symmetrical about zero, as in the example of sine; we can hope this would make any symmetry of the function more visible in the equation itself. This transformation is accomplished by replacing \(x\) with \(x+5\); or equivalently, to avoid confusion, we can use a new variable, letting \(x=t+5\), so that \(t=x-5\). This makes the function $$\frac{5^{\sqrt{10-x}}}{5^{\sqrt{x}}+5^{\sqrt{10-x}}}=\frac{5^{\sqrt{10-(t+5)}}}{5^{\sqrt{t+5}}+5^{\sqrt{10-(t+5)}}}=\frac{5^{\sqrt{5-t}}}{5^{\sqrt{5+t}}+5^{\sqrt{5-t}}}$$ and, since when \(x=2\), \(t=2-5=-3\), and when \(x=8\), \(t=8-5=3\), the new integral is $$\int_2^8\frac{5^{\sqrt{10-x}}}{5^{\sqrt{x}}+5^{\sqrt{10-x}}}dx=\int_{-3}^3\frac{5^{\sqrt{5-t}}}{5^{\sqrt{5+t}}+5^{\sqrt{5-t}}}dt$$
The exponents all differ only in the sign on the variable (\(5+t\) vs. \(5-t\)); when you replace \(t\) with \(-t\), it doesn’t change sign (so it isn’t yet an odd function), but at least the denominator is the same. I haven’t quite led him to the actual solution, but we are getting closer.
Swamy answered:
It’s a question from an entrance exam (for 12th grade students) for universities in my state.
I don’t see the symmetry.
This suggests that it is intended to be challenging (my understanding is that university entrance exams in India are meant to identify truly talented students, much as contests are), but it doesn’t tell us whether the needed ideas have been taught.
Finishing up
Having made little progress, I chose to be more direct now:
Shift the function left by 5 units, so that the center of the domain, [0, 10], moves to x=0. This is what I have been suggesting, but you appear not to have tried.
Here are graphs of the given integrand (red), and the result of shifting left (green):
When you replace x with x+5, the equation for the function will have a more obvious symmetry. To make it even more obvious, you could now shift the function down by 0.5, moving the range from [0, 1] to [-0.5, 0.5]. The graph suggests this symmetry; these changes are one way to confirm it.
Swamy was satisfied; but let’s now do the work I had suggested:
We made that leftward shift from
$$f(x)=\frac{5^{\sqrt{10-x}}}{5^{\sqrt{x}}+5^{\sqrt{10-x}}}$$ to $$g(x)=\frac{5^{\sqrt{5-x}}}{5^{\sqrt{5+x}}+5^{\sqrt{5-x}}}$$
so that the domain and the region of integration would be symmetrical about 0. Our goal at the moment is to prove (or discover, if we hadn’t seen a graph) the symmetry of the function.
What we have now clearly isn’t even; in order for h to be an odd function, we would need \(h(0)\) to be zero; so we can observe that
$$g(0)=\frac{5^{\sqrt{5}}}{5^{\sqrt{5}}+5^{\sqrt{5}}}=\frac{1}{2},$$
and subtract that to shift the function down so that it passes through the origin. This gives a new function,
$$h(x)=\frac{5^{\sqrt{5-x}}}{5^{\sqrt{5+x}}+5^{\sqrt{5-x}}}-\frac{1}{2}\\=\frac{2\cdot5^{\sqrt{5-x}}-\left(5^{\sqrt{5+x}}+5^{\sqrt{5-x}}\right )}{2\left(5^{\sqrt{5+x}}+5^{\sqrt{5-x}}\right)}\\=\frac{5^{\sqrt{5-x}}-5^{\sqrt{5+x}}}{2\left(5^{\sqrt{5+x}}+5^{\sqrt{5-x}}\right)}.$$
We can see that this is an odd function:
$$h(-x)=\frac{5^{\sqrt{5+x}}-5^{\sqrt{5-x}}}{2\left(5^{\sqrt{5-x}}+5^{\sqrt{5+x}}\right)}\\=-\frac{5^{\sqrt{5-x}}-5^{\sqrt{5+x}}}{2\left(5^{\sqrt{5+x}}+5^{\sqrt{5-x}}\right)}=-h(x).$$
Here is its graph:
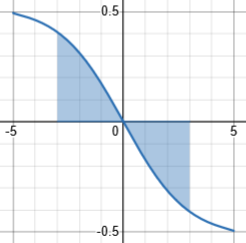
The integral of this is clearly zero; so our integral is (putting everything together) $$\int_2^8\frac{5^{\sqrt{10-x}}}{5^{\sqrt{x}}+5^{\sqrt{10-x}}}dx=\int_{-3}^3\frac{5^{\sqrt{5-t}}}{5^{\sqrt{5+t}}+5^{\sqrt{5-t}}}dt\\=\int_{-3}^3\left(\frac{5^{\sqrt{5-t}}-5^{\sqrt{5+t}}}{2\left(5^{\sqrt{5+t}}+5^{\sqrt{5-t}}\right)}+\frac{1}{2}\right)dt\\=\int_{-3}^3\frac{5^{\sqrt{5-t}}-5^{\sqrt{5+t}}}{2\left(5^{\sqrt{5+t}}+5^{\sqrt{5-t}}\right)}+\int_{-3}^3\frac{1}{2}dt=0+3=3.$$
Alternatively, we could just observe this in the graph that we shifted to the left only:
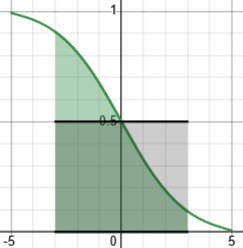
The area under the curve is the same as the area under the horizontal line, which is \(\frac{1}{2}(3-(-3))=3\).
We could also express this in terms of the symmetry of the original function about the point \((5, \frac{1}{2})\):
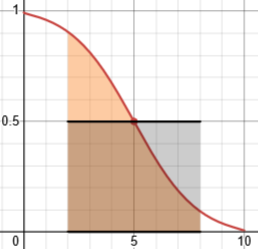
Most of our work was just to convince ourselves, bit by bit, that the apparent symmetry (which we probably wouldn’t have seen without drawing the graph, but can deduce from our transformations) is real. We’ll see a quicker “magical” approach below.
A similar problem from 20 years ago
Knowing this sort of work is not uncommon, I looked through old questions and found one using a similar idea, but presented as a trick method for an advanced problem. This is from 2003:
Integral of dx/(1+(tanx)^sqrt2) Find the value of the integral that ranges from 0 to pi/2 of dx/(1 + (tanx)^S), where S is the square root of 2. I know this question has a solution, but I haven't the slightest idea how to do it. I tried a substitution letting z = 1 + (tanx)^S, and that eventually brought me to a rather interesting fraction after simplifying the trig functions. Nonetheless, no matter what I do, I never arrive at an answer. The exponent on the tan(x) is the square root of 2, so it is intimidating just to look at.
We’re trying to evaluate $$\int_0^{\frac{\pi}{2}}\frac{dx}{1+(\tan(x))^\sqrt{2}}$$
Doctor Pete answered:
Hi Michael, This question is an old Putnam problem, and the solution is very well known. The reason that the exponent S = Sqrt[2] was chosen is so that the integrand is not integrable in closed form. Thus any efforts to try to substitute or transform the integrand will fail.
That’s actually a kindness, preventing the solver from putting too much effort into trying to find an antiderivative! The Putnam exam is a challenging college competition (yes, this is a contest problem!) including many problems that almost no one is expected to solve. (See here.)
The key to solving this question is to use the fact that the integral is definite, and that the integrand obeys a particular property which I will describe presently.
Let’s graph the integrand, to get a preview of what that property might be:
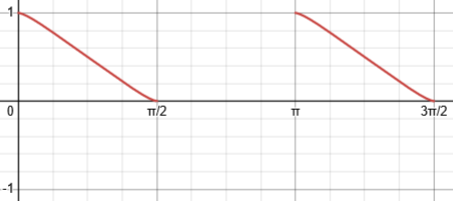
This looks surprisingly like our problem above, except that it is periodic. Do you see a possible symmetry there? Can you, in fact, make a guess as to the value of the integral?
If we consider the substitution of the form
u = Pi/2 - x,
du = - dx,
it is clear that the interval of integration is reversed and the integrand is negated, the total effect of which is that we again arrive at a definite integral over [0, Pi/2].
This is a reflection across \(x=\frac{\pi}{4}\):
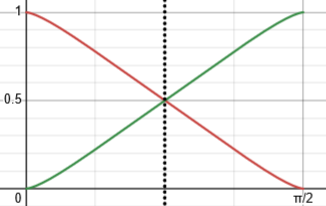
As x goes from 0 to \(\frac{\pi}{2}\), u goes from \(\frac{\pi}{2}\) to 0. The area under the curve is unchanged.
However, the integrand becomes
du/(1 + Tan[Pi/2 - u]^S),
and since
Tan[Pi/2 - u] = Cot[u] = 1/Tan[u],
we find the integrand is
du/(1 + 1/Tan[u]^S).
Now simplify the fraction to obtain
Tan[u]^S du/(Tan[u]^S + 1).
Our new integral is
$$\int_0^{\frac{\pi}{2}}\frac{(\tan(u))^{\sqrt{2}}}{(\tan(u))^{\sqrt{2}}+1}du.$$
This has the same value as the original integral; since it doesn’t matter what we call the variable, we can say
$$I=\int_0^{\frac{\pi}{2}}\frac{1}{1+(\tan(u))^{\sqrt{2}}}du\\I=\int_0^{\frac{\pi}{2}}\frac{(\tan(u))^{\sqrt{2}}}{(\tan(u))^{\sqrt{2}}+1}du.$$
Adding the two equations, we get $$2I=\int_0^{\frac{\pi}{2}}\frac{1}{1+(\tan(u))^{\sqrt{2}}}du+\int_0^{\frac{\pi}{2}}\frac{(\tan(u))^{\sqrt{2}}}{(\tan(u))^{\sqrt{2}}+1}du\\=\int_0^{\frac{\pi}{2}}\frac{1+(\tan(u))^{\sqrt{2}}}{(\tan(u))^{\sqrt{2}}+1}du=\int_0^{\frac{\pi}{2}}1du=\frac{\pi}{2}$$
One should now realize that the value of the integral has not changed, but the integrand takes on a convenient form. In particular, twice the integral's value is simply
1/(1 + Tan[u]^S) + Tan[u]^S/(Tan[u]^S + 1) du,
which is just 1 du. Therefore the integral evaluates to Pi/4.
This is the area of the rectangle here:
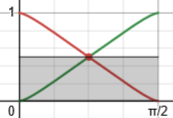
As you can see here, definite integrals can sometimes be evaluated by somewhat non-traditional means, where an indefinite integral would fail. This is because the integrand may satisfy certain special properties over a specific interval of integration. For instance, the integral of
Log[Sin[x]] dx
on [0, Pi/2] is equal to -Pi Log[2]/2, but there is no elementary antiderivative of this integrand.
This integral, using symmetry and a lot more, is discussed in
Finding a Definite Integral with Natural Log and Sine
Michael replied:
Thank you so much! The solution is so very easy, but I would never have thought of that in a million years. This is one of those times when you realize how beautiful math really is. Thank you so much, the answer makes perfect sense to me now!
Once you see the trick, it’s easy!
Redoing our problem
This version of the trick can also be applied to our problem, solving it more quickly. Rather than shifting the function left by 5 units, we can reflect it over the line \(x=5\) by letting \(u=10-x\). (That’s a lot like what Swamy did, but without the square root.) Then we get $$\int_2^8\frac{5^{\sqrt{10-x}}}{5^{\sqrt{x}}+5^{\sqrt{10-x}}}dx=\int_8^2\frac{5^{\sqrt{u}}}{5^{\sqrt{10-u}}+5^{\sqrt{u}}}(-du)=\int_2^8\frac{5^{\sqrt{u}}}{5^{\sqrt{10-u}}+5^{\sqrt{u}}}du$$ But this gives two equal representations of the same integral: $$I=\int_2^8\frac{5^{\sqrt{10-x}}}{5^{\sqrt{x}}+5^{\sqrt{10-x}}}dx\\I=\int_2^8\frac{5^{\sqrt{x}}}{5^{\sqrt{10-x}}+5^{\sqrt{x}}}dx$$ Adding these together, we get $$2I=\int_2^8\frac{5^{\sqrt{10-x}}}{5^{\sqrt{x}}+5^{\sqrt{10-x}}}dx+\int_2^8\frac{5^{\sqrt{x}}}{5^{\sqrt{10-x}}+5^{\sqrt{x}}}dx\\=\int_2^8\frac{5^{\sqrt{10-x}}+5^{\sqrt{x}}}{5^{\sqrt{x}}+5^{\sqrt{10-x}}}=\int_2^8dx=6$$ so \(I=3\). Easy!
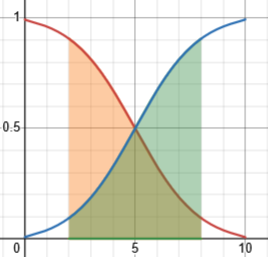
Before, we were exploring, trying to transform our integral into one whose symmetry was obvious; here we have seen that the original function is itself symmetric about the point \((5, \frac{1}{2})\) and used that directly.
This is how many classic solutions work: They start with exploration and somewhat ugly work, but eventually become elegant methods. My hope is that you’ve come to see this trick, not as magic you’d never guess, but as something you could have discovered with the right insights.