(A new question of the week)
Suppose we have a question that can be answered with Yes, No, or Maybe, and that whenever two people with different opinions meet, their discussion convinces each of them that neither can be right, so they both change to the other opinion. Given initial numbers of people with each view, what is the least number of meetings before they can come to full agreement?
Here is the question as asked by Gilad on April 1:
3 groups argue.
Group A has 42 students that agree.
Group B has 36 students that disagree.
Group C has 43 students that say maybe.
When a student from any group meets a student from another group, they both change their answer to the third group’s opinion.
What is the minimum number of meetings needed in order for everyone to take the same stand?
Clarifying and modeling the problem
I had a couple concerns about the meaning of the problem (mostly due to language), so I responded with questions, along with some thoughts:
Hi, Gilad.
I haven’t solved the problem yet, so I can’t give a specific hint, but I’d like to ask you a couple questions, and tell you how I’ve started.
My first thoughts are to clarify exactly what the problem means; perhaps you can tell me if you think I am wrong.
As I understand it, “agree”, “disagree”, and “maybe” don’t refer to whether each group agrees among themselves, but how they would answer some question (such as, “Do you like this weather?”) to which each can say Yes, No, or Maybe.
My first impression of students in a group “agreeing” was that they “agree with one another”; but that doesn’t fit the other two groups! Rather, they all agree, or all disagree, or all are uncertain, about some statement they were asked about.
Also I think the “groups” are not fixed groups of people, but just “all who say yes”, “all who say no”, and “all who say “maybe”. So everyone who says yes (at the moment) is in group A, and so on. Any two people with different opinions may meet, and then they both change their minds to the third opinion.
We could, in fact, just say that there are 121 people, and each person has a label, A, B, or C; and we can, at any step, change any two different labels to the other label.
My first impression of “Group A has 42 students that agree” was that, among students in one pre-existing group, 42 said yes; but, again, that didn’t fit the rest of the problem, so I reconsidered it. The groups are defined by the students’ opinions.
And this led me to change my model of the situation from separate groups of students, to one large group of students, each of whom has a nametag that indicates his opinion. If he changes his tag, he is in a different “group”.
This illustrates how a central part of understanding a problem is to develop a model (that is, a way to think about the problem). But there is not only one possible model; as we’ve seen in combinatorial problems, we may change models several times as we work through a problem.
Another model is just to list the number of people with each label, and at each step subtract 1 from two of the counts and add 2 to the other. So the process might look like this:
A B C 42 36 43 -1 -1 +2 41 35 45 -1 +2 -1 40 37 44and so on. The question we are asked is, what is the minimum number of steps in the process that will take us to a state (0, 0, 121), (0, 121, 0), or (121, 0, 0)? Or, perhaps, is that even possible?
In the example, an A and a B meet and become C, then an A and a C meet and become B. We are representing a state of the system as an ordered triple of numbers.
That suggested a visual model: Each ordered triple could be a point in space; or, since the sum is constant, a point on a plane:
I can imagine also representing any given state by a point on a grid, where ordered pair (A, B) implies that C = 121 – A – B. Only three moves are allowed on the grid, and we are to get from (42, 36) to one of the goals (0, 0), (121, 0), or (0, 121).
We’ll see several of these grids below. The key idea is that we only need to show two of the numbers (I chose A and B), because they imply the value of C. The three possible moves are
- decrease B (and C) by 1, increasing A by 2 (moving “east-southeast”, down and right),
- decrease A (and C) by 1, increasing B by 2 (moving “north-northwest”, up and to the left), or
- decrease A and B by 1, increasing C by 2 (moving “southwest”, down and left).
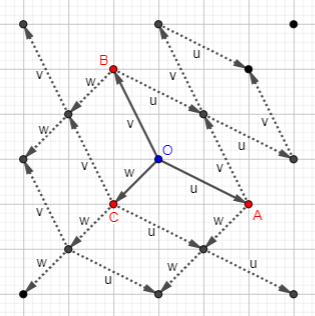
Here are what each of the three moves looks like on the grid, where the horizontal axis is A and the vertical axis is B:
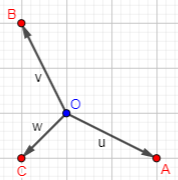
We move from point O to point A when a pair change their position to A, and so on.
While inventing a model, I tend to experiment (play) to see how it works:
I’ve tried playing the game with smaller numbers, starting with (1, 2, 3), and making a diagram of state transitions; it looks like this example can’t reach the goal. That’s why I added the possibility that the answer may be that it is not possible, so there is no minimum. One way to prove that might be to find an invariant that none of the goals satisfy.
All this talk of states reminded me of something!
(Having said that, I realize that our post Invariants for a State Machine may suggest some useful techniques. In fact, I think it’s all you need.)
At this point, I was convinced I had the tools needed to actually solve the problem, so I sent my answer with a closing:
Now it’s your turn. Please answer my questions, and correct my interpretation if you think I’m wrong. Possibly a specific topic you are learning will suggest a way to approach the problem, using one of my models, or something else entirely.
And maybe another of us will have a different idea, in case this isn’t an approach you can handle.
Answers and first attempts
Gilad replied:
Dear Dr. Peterson,
Thank you for your elaborated answer.
You understand correctly, the groups are actually a set of members with the same label.
This is a riddle asked in our work group, I have not come to a single answer yet, I suspected it has no fixed solution and this is the reason I posted here. Some members of my group repeated the steps to move member between groups and got to the number 42 (hint) but did not post the solution yet.
We’ll see that the suggested answer is correct. But we need to convince ourselves. Gilad continued my “playing” by considering all possible “moves” from the given initial state of (42, 36, 43):
Possible transitions from this state:
A student from Group A meets a student from Group B: (A – 1, B – 1, C + 2)
After this meeting: (41, 35, 45)A student from Group A meets a student from Group C: (A – 1, B + 2, C – 1)
After this meeting: (41, 38, 42)A student from Group B meets a student from Group C: (A + 2, B – 1, C – 1)
After this meeting: (44, 35, 42)Analyze the possible transitions from each of these states:
From (41, 35, 45):
A student from Group A meets a student from Group B: (40, 34, 47)
A student from Group A meets a student from Group C: (40, 37, 44)
A student from Group B meets a student from Group C: (43, 34, 44)
From (41, 38, 42):
A student from Group A meets a student from Group B: (40, 37, 44)
A student from Group A meets a student from Group C: (40, 40, 41)
A student from Group B meets a student from Group C: (43, 37, 39)
From (44, 35, 42):
A student from Group A meets a student from Group B: (43, 34, 44)
A student from Group A meets a student from Group C: (43, 37, 39)
A student from Group B meets a student from Group C: (46, 34, 39)
I tried to continue this process iteratively, exploring possible transitions from each state. However, the total number of students remains constant throughout these transitions.
Given this observation, it seems there isn’t a minimum number, however I am not 100% sure of this solution.
In principle, we could continue this list (of possible states after the first move and after the second move) to make a network (that is, a graph, in the sense we discussed in Graph Coloring: Working Through a Proof) of all possible paths through the “state space”; but this would be far too many to actually do. Nevertheless, such “play” can help one think about what is happening … especially if you use a more visual model. Gilad continued:
One possible approach to solve this problem is to construct a graph where each node represents a state (combination of the number of students in each group) and each edge represents a possible transition between states.
We can then explore this graph to identify any cycles or patterns that will help us determine the minimum number of meetings needed for everyone to take the same stand.
Sadly I am not an expert using those tools and could not get further down the solution.
The full answer will be posted in a few days, I will keep you updated!
These, again, are nice ideas to keep in mind (and they reveal how much Gilad knows), but will not be directly fruitful.
Doctor Rick jumped in with a couple ideas; as I had suggested, we like to collaborate on interesting questions!
Hi, Gilad.
I was thinking about this overnight. Thinking globally (rather than step by step), I can see that there must be a minimum of 39 meetings, because at least 36 + 42 minds must be changed, and each meeting changes two minds.
I have come up with a way to accomplish the goal in 42 meetings (if I didn’t make a mistake somewhere). What I can’t do yet is to prove that this is the fewest meetings possible.
We’ll continue to think about it!
It can’t possibly take less than 39 “moves”, because the two smallest numbers in the initial state are 36 and 42, so at least that many minds must be changed, two per step, if two numbers are to be reduced to 0.
But the minimum actually possible may be more than that. Since he has found a way to take 42 moves, the minimum number must be between 39 and 42, inclusive.
Gilad responded:
Interesting!
I tried 39, but whatever I do I get to 42 meetings … that’s easy. But as you mentioned I couldn’t prove that can be done for less than 42 meetings.
Making a model on a spreadsheet
Now I had more to say:
I used the ideas in the post I referred to (finding a pair of invariants), to show that of the three possible goals, (0, 0, 121), (0, 121, 0), and (121, 0, 0), only the first is possible. And it seems clear that this can’t be reached in less than 42 steps.
(If I had shown that none of the goals were possible, it would have been an interesting trick question; the answer would be, sort of, infinity! What did you mean by “it seems there isn’t a minimum number”?)
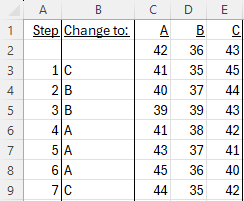
To make this visible, I made a spreadsheet that lets me see the results of any sequence of steps; here is an example of the start of a (bad) sequence:
I enter in column B the group to change to (for example, C tells it to add 2 to C and subtract 1 from A and B, moving “southwest”). Then it plots a path of points as shown here:
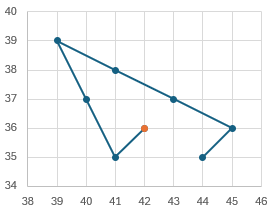
We started at (42, 38), then went “southwest” to (41, 35), subtracting from A and B and adding 2 to the unseen C; then we went “north-northwest” to (40, 37), subtracting 1 from A (and C) and adding 2 to B; and so on.
This doesn’t look like a good way to reach unanimity, does it? To play the game, you need to aim for one of the three goals, which on this graph will look like (121, 0), or (0, 121), or (0, 0).
My claim is that the first two of these are unreachable, and the last can be attained in 42 steps. We’ll look soon at the invariants I used to make that conclusion, but it’s more fun to play the game first! You can find the spreadsheet here:
The strategy for getting to unanimity as fast as possible is obvious (at first); just head straight in that direction. There’s a little twist at the end, though.
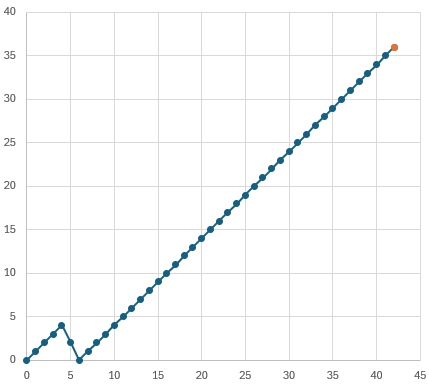
I also made a graph as I suggested, showing the ordered pairs (A, B) along the path starting at (42, 36). Here is the winner:
We could change where we take the two “NNW” steps, but it seems clear that we can’t do any better. I haven’t tried to make this an actual proof.
So there isn’t only one actual path, but every such path will be a rearrangement of the same 42 steps, which in my spreadsheet consists of 40 C’s and 2 B’s. Here is another of those (the x-axis is A, the y-axis is B):
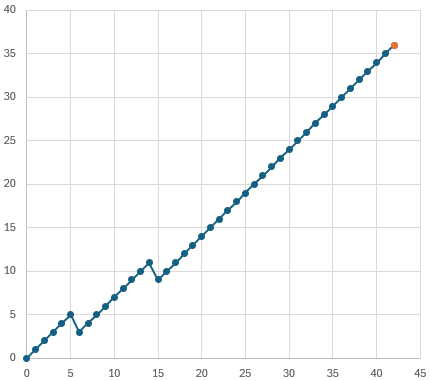
Observe that each move subtracts 1 from A, so it has to take 42 steps to get to 0. But what about the other two goals?
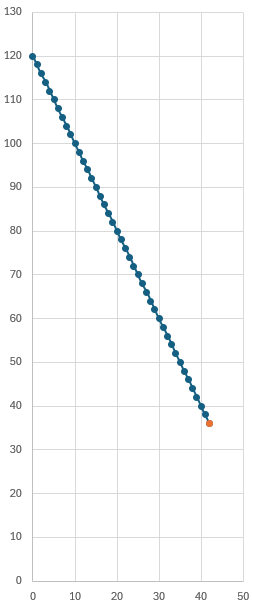
Here is an example of failure to attain one of the other goals (again, 42 steps):
Each step here (adding 2 to B, subtracting 1 from A and C) moves to the “north-northwest”, reducing A from 42 to 0; but we end up with 120, not 121, for B, because there is still 1 in group C. It seems clear that we can’t do any better; but my claim is that we can never get to (0, 121, 0) at all.
Gilad replied:
This is a math riddle still on progress that was asked in a Math forum in Israel.
I was unsure about the solution so needed an expert opinion, and you definitely shed some light on the need to prove – which I struggled with.
Since there was no credit riding on it; I could feel free to say more (but still not give a full solution).
Solving the problem
I answered:
I should probably make it explicit that a complete proof is implicit in what I’ve said. It’s obvious that if we are to end with 0 saying yes, then we have to reduce A from 42 to 0, which can take no less than 42 steps; and I’ve mentioned that I can prove, using a pair of invariants, that the other possible goals (including increasing A to 121) can’t be accomplished at all. I’ve left that part for you to do, following the post I referred to, or whatever other knowledge you have.
We’ve also seen that we can’t increase B to 121 in less than 42 steps, because that would require adding 2 to B at least \(\frac{121-36}{2}=42.5\) times. But we can show more than that.
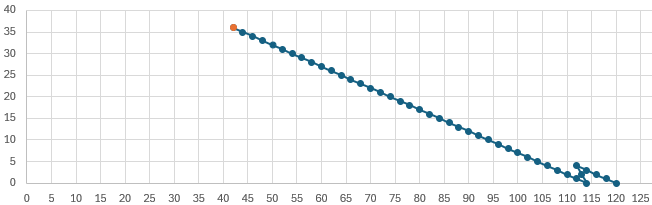
For completeness, here’s the best I could do for that goal (again, x is A, y is B):
This reaches 120 in 42 steps; but it isn’t so obvious we can’t reach 121.
This is where the invariants are necessary to convince you it’s impossible.
We didn’t hear back about the solution; but let’s look into this matter of invariants.
Using invariants to make a proof
If you’ve taken the bait and looked at Invariants for a State Machine, then you will have seen how Doctor Jacques found and used invariants to show that a goal was unreachable; if you haven’t, go read it. I’ll wait …
So how do we find invariants for our problem?
We’ll try by inspection to find an invariant or two: expressions that must remain the same after any move. We’ll stick with my graphs of (A, B), which I’ll now call \((x,y)\), rather than work with all three variables (since \(x+y+z=121\) is itself an invariant).
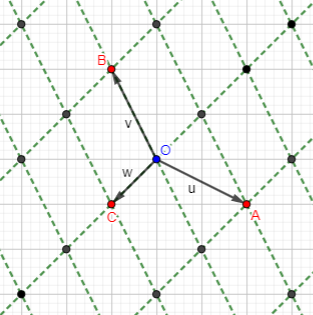
First, observe what the three moves look like graphically; each is a vector:

Also, note that \(u+v+w=0\), so they are not independent, and we can use only two of them:
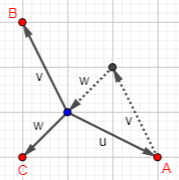
Now consider all sums of these vectors:
The accessible points (relative to whatever point we start at) are the lattice points (integer coordinates) on the lines \(y-x=3m\) and \(2x+y=3n\):
So we can define two invariants: \(\alpha=x-y\) and \(\beta=2x+y\) always remain the same (modulo 3); that is, they always change by a multiple of 3. So a point is reachable if, and only if, \(\alpha\) and \(\beta\) differ from their original values by a multiple of 3.
Now, our starting point is (42, 36), for which \(\alpha=42-36=6\) and \(\beta=2(42)+36=120\) are both multiples of 3; so any reachable point must do the same. We have three possible goals:
- (0, 0):
\(\alpha=0-0=0\)
\(\beta=2(0)+0=0\)
This is reachable. - (121, 0):
\(\alpha=121-0=121=3(40)+1\)
\(\beta=2(121)+0=242=3(80)+2\)
This is unreachable because the remainders are not both 0. - (0, 121):
\(\alpha=0-121=-121=3(-40)-1\)
\(\beta=2(0)+121=121=3(40)+1\)
This is unreachable because the remainders are not both 0.
So only the first goal is reachable, and we have seen that it requires 42 steps, so the answer is confirmed.
Now, you might want to play with the problem itself, by changing the starting point. Can you make one from which we can reach unanimity in more than one way?