A Tunnel Through the Earth

I have a very short problem this week: How deep will you go if you dig a straight tunnel through the earth, how long will it be, and what angle do you have to start at?

How can we aim the tunnel?

Here is the question, from Carson at the end of October:

Say one digs a tunnel through the Earth.  The angle of descent determines the egress point and depth of the tunnel.

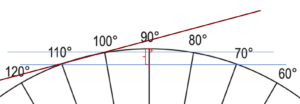
Starting from the surface, how would one determine the angle to dig if they wanted to enter at 100° and exit at 80°?  or 110° to 70°?

How would one determine the depth of the deepest point [the 90-degree point]?

Another way to question this would be, “If one were to dig a tunnel at 10° into the Earth, starting at the 100° point, and digging a straight line, how would they determine the degree point where exiting?  How would they determine the length of the tunnel?  How would they determine the tunnel’s greatest depth from the surface?”

Thank you for your help.

Carson

The question was actually spread out over three initial messages, and the question became clearer as they came in! There are really several questions here: Given the destination, what direction will you be digging, and how deep will you go? Given the direction, what will be the destination, distance, and depth?

What do those angles mean?

I answered:

Hi, Carson.

I’m glad you included the picture, because I was very confused at first — I thought the angles you listed were angles of inclination (“enter at 100°” as a direction), which made no sense. But they are apparently locations, something like longitudes (if you were on the equator).

My first thought is that all that matters is the difference in the locations, which is the measure of the arc you are subtending. For example, digging from 110° to 70°, you subtend a 40° arc.

The specified longitudes on the equator are not on land (the closest being a tunnel from Thailand to Sri Lanka under the Indian Ocean); on another parallel of latitude, distances corresponding to a given angle would be smaller, and longitudes would not correspond to angles along a great circle route. We could also use locations on the same longitude line , but latitudes are not measured greater than 90 degrees, so that doesn’t fit his example.

But a 40 degree arc amounts to any distance of about 2765 miles on the surface, and 20 degrees to about 1382 miles. The former might be from Bellingham, Washington, to Miami:

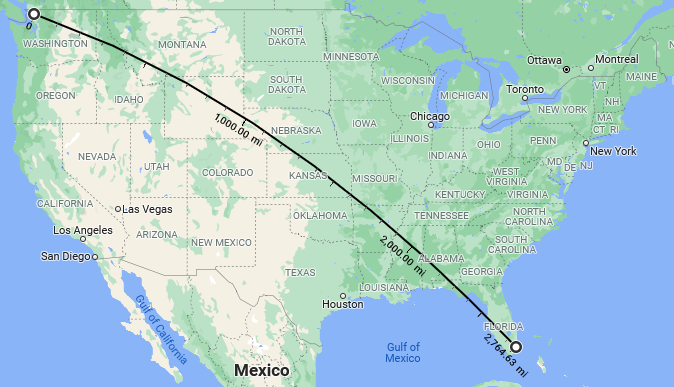
… and the latter from Cody, Wyoming, to Meridian, Mississippi (the middle half of that route):

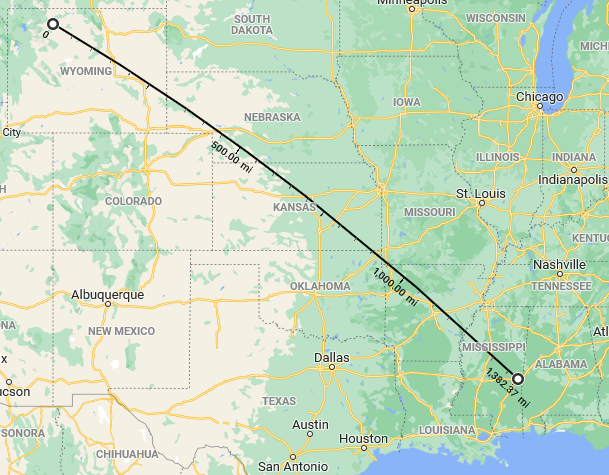
The route is a Great Circle, which appears curved on a map; thanks to Google Maps for the nice tool!

We wouldn’t normally talk about this as covering 40 degrees of the earth, or identify the start and end points by angles like 110°; but I think this is the best interpretation we can make for the question. Picture slicing the earth with a plane through the center and both end points, and then marking off degrees on the resulting circle, and it will fit what he asked.

Formulas for length and depth

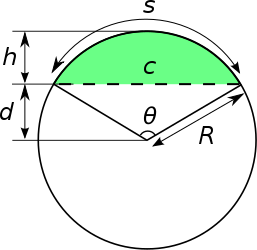
The length of the tunnel is a chord (c), and the greatest depth is the height (sagitta, h), of the arc, as shown in Wikipedia:

The angle at which you start digging would be θ/2, where θ is the measure of the arc (e.g. in my example above, θ = 40°, so you would start digging at 20° to the surface).

The formulas for c and h are given in the Wikipedia link, in terms of known values of R and θ.

The formulas as shown in Wikipedia are as follows:

The chord length is $$c=2R\sin{\frac{\theta}{2}}=R{\sqrt{2(1-\cos\theta)}}$$

The sagitta is $$h=R\left(1-\cos{\frac{\theta}{2}}\right)=R\left(1-{\sqrt{\frac{1+\cos\theta}{2}}}\right)$$

Let’s make our own picture, so I can better explain these answers, and the formulas:

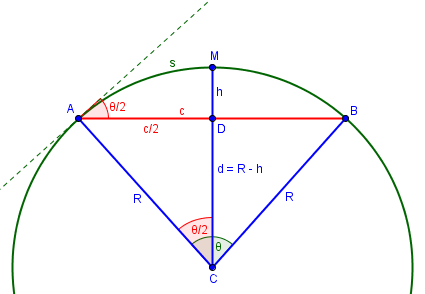
Incidentally, this picture shows the reason for some of the names of its parts. The word “arc” (s) originally meant “bow” (as in archery); “chord” (c) meant “cord” or “string”; and “sagitta” (h) meant “arrow” (as in the constellation Sagittarius, the archer). Can you see the latter nicely fitting to the string before being pulled back?

From right triangle ADC, we see that $$\sin{\frac{\theta}{2}} = \frac{c/2}{R} = \frac{c}{2R},$$ and solving this for \(c\) gives the first formula above.

Also from ADC, $$\cos{\frac{\theta}{2}}= \frac{R-h}{R} = 1 – \frac{h}{R},$$ which we solve for \(h\) to get the second formula.

The alternative forms come from the half-angle formulas for sine and cosine.

Other, related formulas (but involving only distances, not angles) are discussed in the article How Much Does the Earth Curve?

The digging angle

And why is the angle at which we dig \(\frac{\theta}{2}\), as I said, and as shown in the diagram above? One way to see this is that \(\angle CAD\) is the complement of \(\frac{\theta}{2}\), and the angle between the chord and the tangent is the complement of that. The complement of the complement is the original angle.

This leads to the answer to his second form of the question:

If you start digging at 10° to the surface, then you know you will come out 20° from the start (that is, 20/360 = 1/18 of the circumference of the earth). Of course, this depends on being able to dig in an exact line maintaining that direction.

You’d probably need to use some sort of laser beam to keep the tunnel straight; the slope, as measured by a plumb line or level, would be constantly changing as you reach “bottom” and start climbing “uphill” while still going straight!

Interestingly, this tells us that the distance (as measured along the ground) from start to exit is proportional to the angle at which you dig — all the way until you dig vertically, 90 degrees from horizontal, and come out 180 degrees from the start. The linear distance, of course, is not at all proportional.

Incidentally, the fact that the angle is half the angle subtended is an instance of the third theorem here:

https://mathbitsnotebook.com/Geometry/Circles/CRAngles.html

This site lists several “circle theorems” relating angles between chords, tangents, and secants of a circle to the central angles of the arcs intercepted. Our case is essentially identical to the “tangent-chord angle theorem”.

More on the two examples

Let’s look at our two examples. The radius of the earth is \(R\approx 3,960\) miles (depending on how you measure it; see here for details). Using that, and converting angles to radians as needed:

From Bellingham to Miami, with \(\theta=40^\circ\), the surface distance is \(\frac{40^\circ}{180^\circ}\pi\cdot 3960\approx 2765\text{ miles}\approx 4450\text{ km.}\)

The tunnel length is \(c=2(3960)\sin{\frac{40^\circ}{2}}\approx 2709\text{ miles}\approx 4355\text{ km.}\)

The tunnel depth is \(h=3960(1-\cos{\frac{40^\circ}{2}})=239 \text{ miles}\approx 385\text{ km.}\)

From Cody to Meridian, with \(\theta=20^\circ\), the surface distance is \(\frac{20^\circ}{180^\circ}\pi\cdot 3960\approx 1382\text{ miles}\approx 2224\text{ km.}\)

The tunnel length is \(c=2(3960)\sin{\frac{20^\circ}{2}}\approx 1375\text{ miles}\approx 2213\text{ km.}\)

The tunnel depth is \(h=3960(1-\cos{\frac{20^\circ}{2}})= 60\text{ miles}\approx 97\text{ km.}\)

The shorter tunnel is about half as long (and quite close to the surface distance), but ¼ as deep. This is expected, as the cosine behaves like a parabola near its peak. Here is what the two tunnels look like, drawn to scale, echoing Carson’s own drawing:

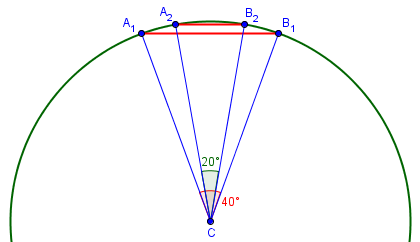
Earth’s crust extends something like 20 to 30 miles under continents, so both tunnels would go into the mantle. Temperature and pressure would be somewhat uncomfortable!

Postscript

After writing this, I had a nagging sense that it reminded me of something, and I finally remembered what it was: The Alameda-Weehawken Burrito Tunnel, which I read about a year ago. The story is well worth reading (especially in early April). This incredible high-speed tunnel is a little shorter than our 40 degree tunnel (which might go from San Francisco to Bangor rather than New York City):

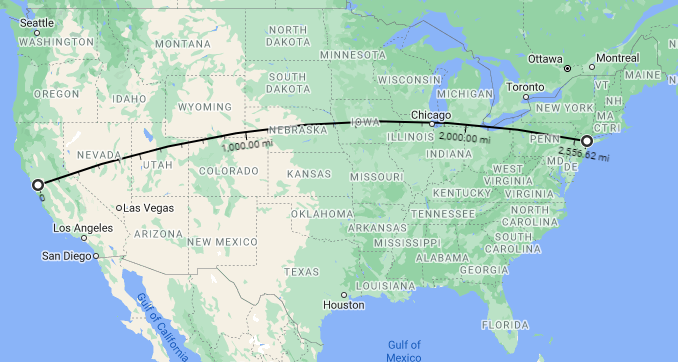
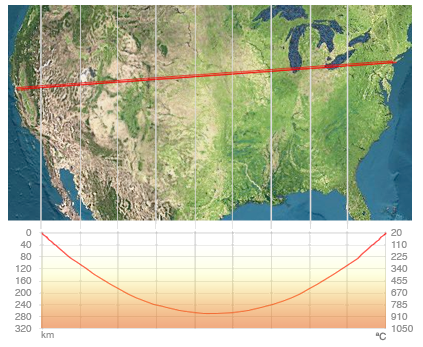
The story includes length and depth information, the latter in a graph:

In 1911, the celebrated British civil engineer Basil Mott approached the plutocrat Andrew W. Mellon with an audacious plan to build a straight-line tunnel 2500 miles long connecting New York City with San Francisco, allowing packages to be sent between the two cities using only compressed air and gravity. The tunnel would resemble the pneumatic tube systems that had served New York City and Paris so well for mail delivery, but on an incomparably vaster scale. …

You may initially think that the map is wrong, showing a straight line; but if you look closely, you’ll see that it is simply a different projection, in which this great circle appears straight. Let’s see how the fiction compares to our formulas.

We can repeat our calculations from above:

The central angle subtended is \(\theta=\frac{s}{R} = \frac{2557}{3960}=0.6457\text{ rad}=37^\circ\).

The tunnel length is \(c=2(3960)\sin{\frac{37^\circ}{2}}\approx 2513\text{ miles}\approx 4044\text{ km.}\)

The tunnel depth is \(h=3960(1-\cos{\frac{37^\circ}{2}})=205 \text{ miles}\approx 330\text{ km.}\)

The reported length of 2500 miles is reasonably accurate. The graph above shows a slightly lower maximum depth of about 270 km rather than 330. The story also correctly notes that the tunnel dips into the asthenosphere (which extends from 100-200 km down to about 700 km), which is part of the upper mantle. But I think the temperatures in the graph are underestimates. You don’t really want to go that deep, and the rock is not rigid there.

You may also want to think about the accuracy of the shape of the graph. I’ll leave that as an exercise for the reader.

For a modified and extended version of the story, watch this video. They got the depth about right, and added more science. As for the history … have fun with it!