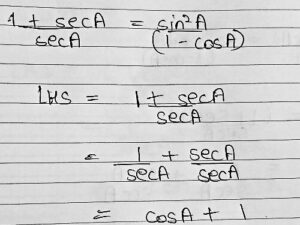(A new question of the week)
Proving a trigonometric identity can be a challenge; sometimes even when we read someone else’s proof, we can fail to see how they came up with a seemingly magical step. We’ll look at two such identities here, and consider how to bridge a gap when we are stuck.
Identity #1: Try working on the right
This question came from Simran in mid-September:
Hello math doctors,
(1 + sec A)/sec A = sin2A/(1 – cos A) in this question I was told to solve the LHS:
I do not understand what to do after cosA + 1 step can you please help me further on this?
Doctor Rick answered, gently correcting the word “solve”:
Hi, Simran.
Your problem is to prove a trigonometric identity. You may find the blog on this topic to be helpful:
Different Ways to Prove a Trigonometric identity
Though you were told to start on the left-hand side, it is often a good idea to look at both sides in order to decide where to go. You’ll see in the blog that we can think of an identity as a “bridge” between the left-hand side and the right-hand side. The best way to write the proof is starting from one side of the “bridge” and “walking” across to the other side, proving that the two sides are connected by valid steps (each step showing two expressions to be equivalent). But in coming up with the proof, we can do as bridge builders do: start from both sides and work toward the middle.
What can you do with the right-hand expression, sin2 A / (1 – cos A)? Do you know any basic trig identity that can be applied to part of that expression? If you can’t think of one right away, tell me what you have learned so far — what sort of trig identities you are familiar with. Then, together, we can look for a way to proceed.
Here are two additional references containing similar ideas:
Proving an Identity in Different Ways
The Art of Proving Trig Identities
And for the bridge idea in geometry proofs, see
How to Write a Proof: The Big Picture
Crossing the bridge both ways
Simran replied, doing the entire proof in both directions:
I checked the RHS and found it. I have attached the picture for you to check if I am right.
Then I found that in order to have sin²A / (1 – cosA) on LHS, we will need to multiply 1 – cosA to the denominator and numerator but are we allowed to do that? I did it while solving but I am doubtful because if we are multiplying the LHS shouldn’t we do it for RHS too since if we multiply just on LHS it changes the actual identity we were given to prove.
Thank you, the blog was really informative. I will definitely try solving the trigonometry identities from both sides.
Thank you for informing about the site.
The word “solve”, which he uses again here, is not really appropriate, and may be leading him to think of the work as if he were solving an equation. But the work is excellent.
Doctor Rick acknowledged this:
What you have done is good. You have essentially shown two proofs of the identity, one going in each direction.
What you did in multiplying the expression (cos A + 1) by (1 – cos A)/(1 – cos A), was perfectly valid, because the expression you multiplied by is just another name for 1, and multiplying any quantity by 1 results in the same quantity you started with. In other words, it results in an equivalent expression – just what we want to do here.
Unveiling the magic
How did he know to do that? He knew to do it when starting from the left, because of what he had discovered when starting from the right.
What seems odd about this sort of thing is that it’s not something you would have thought of while working in this direction – to a reader who has not tried the problem himself, it looks like you “pulled it out of thin air” as we say – like a magic trick. But you and I know where we got the idea – by having worked it backward first!
You have learned in the past how to “simplify an expression” – for instance, by “canceling” like terms in the numerator and denominator, as you did when you canceled (1 – cos A) in your work starting from the RHS. When something like that is done in reverse, you aren’t “simplifying”, you are “complicating” the expression! But it’s just as valid mathematically.
As long as the new expression is equivalent to the original, and somehow leads toward to goal, it is good. The latter may not always be obvious at first!
(While I was editing this, I heard a podcast saying that woodpeckers find food in the bark of a tree while working their way up a tree, while nuthatches do so while climbing down. Each finds food the other misses. Sound familiar?)
Identity #2: How did they get that?
The next day, Simran wrote with a similar question, this time asking about a provided answer:
Hello math doctors,
Sorry but I have one more doubt regarding another question. I have attached the picture of that question along with the solution. When I checked the answer I could not understand how after this step (sin⁴A + cos⁴A) / (cosA × sinA) we arrived on [(sin²A + cos²A)² -2(sin²A.cos²A)/(sinA.cosA)?
Can you please help me out on this?
How did they decide to add and subtract \(2 \sin^2A\cos^2A\)? And then how did they know to rewrite the first three terms as they did?
Doctor Rick replied:
You didn’t show the problem, but I assume it is to prove the identity:
(tan3 A)/(1 + tan2 A) + (cot3 A)/(1 + cot2 A) = sec A cosec A – 2 sin A cos A
This is very similar to the first identity proof you asked about! In the step you asked about, the quantity 2 sin2 A cos2 A is added and then subtracted – this amounts to adding 0, which leaves the value of the expression unchanged. But as before, when you multiplied and divided by the quantity (1 – cos A), I said it would look like magic if you hadn’t worked it out yourself – by working backward from the RHS of the identity.
So … have you tried working backward this time? Maybe you’ll discover where the “magic” step came from!
Book answers can’t always explain every detail; that’s unfortunate, but it gives you the chance to explore and learn more than if you had been spoon-fed every detail.
But … in working backward through the given solution, you will again encounter a bit of “magic”: replacing 1 with (sin2 A + cos2 A)2. These are clearly equal, but how could we have chosen to make this particular substitution??
This is where we really benefit from working from both sides at once! Working from the LHS, we have arrived at
(sin4 A + cos4 A)/(cos A sin A)
while working from the RHS we have arrived at
(1 – 2 sin2 A cos2 A)/(sin A cos A)
Now we want to find a link between the numerators (the denominators are already the same). That is, we want to prove that
sin4 A + cos4 A = 1 – 2 sin2 A cos2 A
Can you see how to prove this?
In order to fill in this gap in our bridge, we need to do something other than merely simplifying each side as we’ve been doing.
What to do when neither direction is obvious
Simran wrote back, trying to prove this new little identity by the same approach:
Actually I tried doing the RHS but I didn’t understand what to do as it seemed more complicated than LHS:
sin⁴A + cos⁴A = 1 – 2sin²A cos²A
sin⁴A + cos⁴A = sin²A + cos²A – 2sin²A cos²A
= sin²A + cos²A – 2sin²A cos²A + 2sin²A cos²A
= sin²A + cos²A
I am confused what to multiply in order to get sin4A + cos4A because I can’t multiply sin²A + cos²A, otherwise it will become sin⁴A + 2sin²Acos²A + cos4A. And I applied the adding and subtracting here to make the value 0 but in the picture I had shared they did not write it as 0, instead they wrote -2 sin²Acos²A. Can you tell how this came?
Doctor Rick replied:
Hi, Simran. You wrote:
Actually I tried doing the RHS but I didn’t understand what to do as it seemed more complicated than LHS
To me, both the LHS and the RHS of the identity to be proved seem “complicated”; that’s a reason to try working from both sides toward the middle. (As I said, that’s how a bridge is built.)
I too wouldn’t know what to do with the LHS. If it were a difference of fourth powers rather than a sum, there would be something I could do there; I could factor it. But not here.
Simran’s attempt was a little confused:
However, I can’t follow what you said you did:
sin⁴A + cos⁴A = 1 – 2sin²A cos²A [we want to prove this — I’d put “=?”, not “=”]
sin⁴A + cos⁴A = sin²A + cos²A – 2sin²A cos²A
= sin²A + cos²A – 2sin²A cos²A + 2sin²A cos²A [you added something (not 0) to one side — wrong!]
= sin²A + cos²A [… so of course you didn’t get what you wanted]
Then you said,
I am confused what to multiply in order to get sin²A + cos²A because I can’t multiply sin²A + cos²A otherwise it will become sin⁴A + 2sin²Acos²A + cos²A. And I applied the adding and subtracting here to make the value 0 but in the picture I had shared they did not write it as 0, instead they wrote -2 sin²Acos²A. Can you tell how this came?
When you say you “applied the adding and subtracting here”, you didn’t do it correctly, because you only added 2 sin2A cos2A; the –2 sin2A cos2A was already there. But in fact, you say something here that will be very useful! You say that
(sin2A + cos2A)2 = sin4A + 2 sin2A cos2A + cos4A [1]
Hold that thought!
Changing tactics
Rather than casting about to find a way to change one side into the other, we can change tactics, and do what is commonly forbidden in final proofs:
Although it is often said to be wrong to treat an identity as you would an equation to be solved – by doing the same thing to both sides to produce an equivalent equation – I mentioned before that this can actually make a valid proof. And in this exploratory stage especially, it’s a good idea. I recommend trying that: Pretend you’re just trying to solve the equation
sin4A + cos4A = 1 – 2 sin2A cos2A [2]
for A. We’ll be hoping to find that any value of A makes the equation true.
If I “move” the last term on the RHS to the left (by adding 2 sin2A cos2A to both sides), I get
sin4A + cos4A + 2 sin2A cos2A = 1 [3]
Now, do you recognize that the LHS of [3] is the same as the RHS of your equation [1]? So, using [1], we can rewrite [3] as
(sin2A + cos2A)2 = 1
But we know this is true for all A! So, in a sense, we are done: we’ve proved that equation [2] is an identity, and that fills the gap in our proof.
Since you are expected (I believe) to prove identities by working from one side to the other (“walking across the bridge”), we have one more task: to rework this exploration (or “bridge-building”) into a “walk across the bridge”. Give that a try; we have all the pieces now, so it’s just a matter of putting them together in the right order.
Putting it all together
After some more discussion, Doctor Rick summarized:
You already have a solution to the problem, and you are just trying to understand how one could have come up with that proof. Let me go over what we have done so far, and then go the rest of the way.
First we explored to find a “path” from the LHS of the identity to the RHS. I like to set up my work on this phase in two columns, one starting with the LHS and the other with the RHS. I don’t put an equal sign between them, because we don’t yet know that they are equal! But all the expressions in the left column are equivalent, and all the expressions in the right column are equivalent.
tan3 A cot3 A ------- + ------- sec A cosec A - 2 sin A Cos A = 1+tan2A 1+cot2A sin3 A cos3 A 1 ------ ------ ----------- - 2 sin A cos A = cos3 A sin3 A sin A cos A = -------- + --------- sec2 A cosec2 A 1 - 2 sin2 A cos2 A ------------------- sin3 A cos3 A sin A cos A = ------ + ------ cos A sin A sin4 A + cos4 A = --------------- sin A cos AI’ve shown (mostly) the same steps as the proof you showed, assuming that you understand it all.
Now we’re stuck, unless we stumble upon a brilliant insight! Lacking that, we focus on the gap and solve:
At this point I’ve taken each side as far as I could this way. What we’d like to do is to be able to put an equal sign between the bottom two expressions; then we’d have a complete chain of equalities (identities, actually) that takes us down the left column, across to the right, and up the right column in a big U. That chain would be the proof we seek — a “walk” across the bridge we just built, from one side all the way to the other.
So now we look for a way to show that the bottom expression in the left column is equal to the bottom expression in the right column. As I said, we already see that the denominators are the same, so we need to prove:
sin4 A + cos4 A = 1 – 2 sin2 A cos2 A
I will show you again how I see to do this. First I add 2 sin2 A cos2 A to both sides (which gets rid of it on the right, as 2 sin2 A cos2 A – 2 sin2 A cos2 A = 0).
sin4 A + cos4 A + 2 sin2 A cos2 A = 1
Now I notice that the LHS can be rearranged to
sin4 A + 2 sin2 A cos2 A + cos4 A = 1
which, as you observed, is the expanded form of (sin2 A + cos2 A)2. So the equation we wanted to solve is equivalent to this:
(sin2 A + cos2 A)2 = 1
But we know that sin2 A + cos2 A = 1 for any A (the Pythagorean identity), so the equation above is true for any A. Therefore we have established that
sin4 A + cos4 A = 1 – 2 sin2 A cos2 A for any A
and the proof is complete.
… except that the proof doesn’t yet look the way we want it to:
But how can we rearrange this latter proof to the “preferred” form, starting from one side and transforming it into the expression on the other side? Let’s do that. I’ll start on the left:
sin4 A + cos4 A = sin4 A + cos4 A + 2 sin2 A cos2 A – 2 sin2 A cos2 A = sin4 A + 2 sin2 A cos2 A + cos4 A – 2 sin2 A cos2 A = (sin2 A + cos2 A)2 – 2 sin2 A cos2 A = 1 – 2 sin2 A cos2 AThere, we’ve done it! Maybe more important, we now know why, in the solution you showed, the quantity in red above was added. As I have said several times, this sort of thing seems like magic until you’ve worked it out for yourself. I hope you can see now how this idea came out of the exploration phase of my work.
This was a tough trig identity, to be sure. But tough challenges are an opportunity to learn things that we couldn’t learn by just following memorized methods or reading predigested solutions.
Parting words
Generally I would start on the more complicated side, so that much of the work of “proving” would consist of simplifying expressions. As I showed, though, sometimes we need to make an expression more complicated rather than simpler in order to get to our goal.
As we are working on one side of the identity, we want to keep that goal in mind – which is to make what we’ve got look like the other side. One reason for working from both sides toward the middle is to make our goal simpler, so that it’s easier to recognize what needs to be done to reach that goal.
Proving identities is an art, learned by experience. (Problem solving in general is an art.) I have shown you some tools we have for proving identities; they include the idea of treating an identity as an equation to be solved, and various other methods that either I or the blog have pointed out now and then. Which tool to use in a particular case is up to you, and that is where the art comes in.
Each identity we work on can teach us a new trick. That is part of the adventure of trigonometry.