(A new question of the week)
Last week we examined how a series of transformations affects the equation of a function, in order to write the equation from a graph, or vice versa. We touched on why it works the way it does, but this is something you need to look at from multiple perspectives in order to really grasp it fully. Luckily, some people don’t stop asking until they get it!
Please tell me more
A month after the question we looked at last week, Mario wrote again, asking about the post from 2019 that I’d referred him to:
I am reading this article from the math doctors: Combining Function Transformations: Order Matters
I have a question on something that was said there. Namely:
You can perform transformations in any order you want, in general. But in this case, you are asking in which order to do them in order to transform f(x) into a specific goal, f(ax+b). The order makes a difference in how you get there. What I do is to explicitly write the steps, one at a time. Suppose we first do the horizontal shrink f(x) -> f(ax). If we then apply a horizontal shift (translation) b units to the left, we would be REPLACING x in f(ax) with x+b, and we'd get f(a(x+b)). That is NOT what we are looking for; it's equal to f(ax+ab). So this order of doing those particular transformations is wrong.The part that confuses me is if you do the horizontal shrink and then you do the horizontal shift, you end up with f(a(x + b)) and not f(ax + b). The reason it confuses me is because it doesn’t concur with how I have come to think about graph transformations.
Let’s say I have a function f(x), and I graph it. I shrink it horizontally by a factor of 1/3. The function now looks like f(3x), and the graph has gotten thinner. Now, let’s say I shift the graph 4 units to the right. I would think the graph would look like f(3x – 4). The reason I think it looks like that is because of the order I transformed the graph. Since I shrunk it first and then shifted, I would add -4 not to the set of inputs x, but to the set of inputs multiplied by 3, thus f(3x – 4). So my question is, what’s my mistake?
This is a very common mistake, and although in principle what I said last time should explain it, it takes several exposures, from different perspectives, to fully understand it, because it is counterintuitive, and your wrong intuitions have to be replaced by correct ways of thinking. (I’m reminded of my early post When Math Doesn’t Make Sense.) Students who pay more attention to memorized procedures than to reasons may just accept what they’re taught, but those who want to understand, like Mario (and me) need more! So I was happy to try again.
A similar example from the 2019 post
I responded:
Hi, Mario.
It happens that I am currently working on turning our previous discussion on this subject into a post. If this answer works well, I’ll try to add it on, because it’s a good follow-up, and I can say some things I’d wished I said.
I did a very similar example to yours late in that post, in the section headed “Looking at the graph”, which you should read carefully.
There we get f(3x – 9) by first shifting (9 units right) and then shrinking (by 1/3). We do that by first replacing x with x – 9 to accomplish the shift, giving f(x – 9), and then replacing x with 3x to accomplish the shrink, resulting in f(3x – 9). I subsequently show that we can get the same thing in your order, shrinking and then shifting by only 3 units, and get f(3(x – 3)).
This differs from your example only in using 3 rather than 4.
There, and last week, I mostly just asserted that the transformed function is constructed by replacing x with something. We want to move beyond mere assertion to answer the deeper “why“.
First, here are the graphs from that post. When we shift first, resulting in the purple graph, and then shrink to make \(f(3x-9)\), the blue graph, it looks like this:
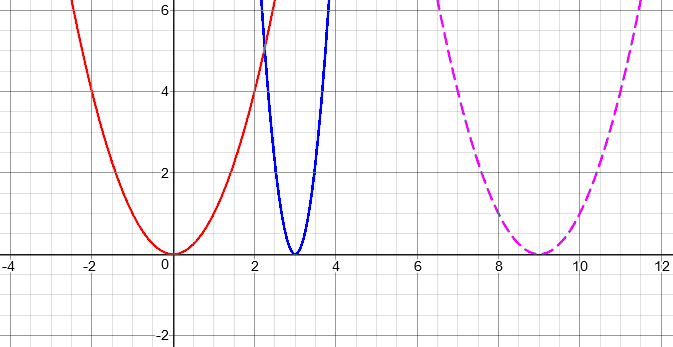
On the other hand, if we shrink first, to make the purple graph, then shift to make \(f(3(x-3))\) in blue, we have:
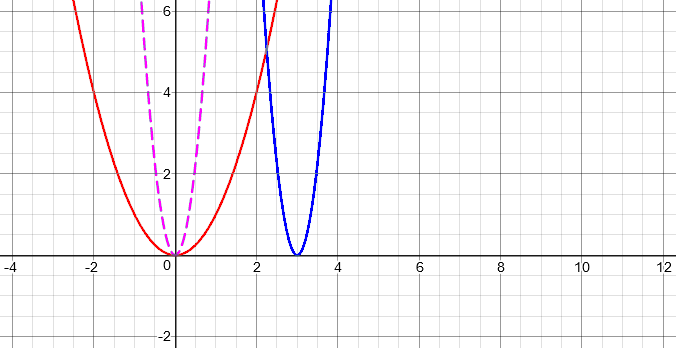
That shows that the result is right (especially if you take the time to verify points on each graph). But this time, I don’t want to depend on graphs to see merely what is right; our goal is to understand the underlying algebra, to see why it is right. We need to have more to say than, “If you don’t believe me, trust the graph.”
Why we replace x
To answer the present question, I referred back to an earlier post that was just about individual transformations, which laid the foundation for combinations of transformations.
Back to your transformations: If you first shrink by 1/3 and then shift right 4 units, you change f(x) first by replacing x with 3x, making it f(3x), and then replace x with x – 4, making f(3(x – 4)). What you said, giving f(3x – 4), is wrong, because you are thinking “forward” rather than “backward”, and we must do everything about horizontal transformations “backward”!
I discussed this “backward” idea in a one-transformation-at-a-time setting in the post before the one you’re reading,
Shifting and Stretching Graphs
There, too, I emphasized the idea of replacement, and explained why we must think of it this way using several different approaches.
In the last post, I used replacement of \(x\) with \(cx\) or \(x-c\) as the foundation, but failed to explain why that was correct. To fill that gap, we can follow a specific point through the successive transformations:
Let’s look more closely at your example, and see how it works. As I did in the “Looking at the graph” section, I’ll take the original function to be f(x) = x2, and use g for the transformed function.
Now, let’s consider a particular point on the original graph, say (3, 9). Applying your transformations to this point in order, we first shrink horizontally, which divides x by 3 and brings us to the point (1, 9). Now we shift 4 units to the right, adding 4 to x and taking it to (5, 9). So our transformed function g should yield g(5) = 9.
First, we can test both claimants to the title of transformed function. First, yours, f(3x – 4):
g(5) = f(3(5) – 4) = f(11) = 112 = 121
That didn’t work!
Now, mine, f(3(x – 4)):
g(5) = f(3(5 – 4)) = f(3) = 32 = 9
That did work. So we’ve demonstrated that your work was wrong.
How it works: solving for x
We’ve now seen, in several ways, that his intuition is wrong; we need to retrain that intuition by seeing clearly what really happens.
Now, why did mine work? Look at what happened: We needed to transform the new x, 5, to the original x, 3, so that f(3) would give us the correct value of y.
We obtained 5 from 3 by applying the transformations in order: starting with 3, dividing by 3 to get 1, and adding 4 to get 5. That is, the new input to the function is x’ = (1/3)*3 + 4 = 5. In general, a point (x, y) transforms to (x’, y) = ((1/3)x + 4, y).
Since what I called x’ is the input to the new function, g, corresponding to the input of x to the original function, f, we want
g(x’) = f(x),
that is, we want
g((1/3)x + 4) = f(x).
But we want an expression for g(x), so we have to solve for x in terms of x’:
x’ = (1/3)x + 4
x’ – 4 = (1/3)x
3(x’ – 4) = x
So our new function is
g(x’) = g((1/3)x + 4) = f(x) = f(3(x’ – 4))
Here, x’ is a dummy variable that we just used as a temporary name; replacing it with the usual x, we have
g(x) = f(3(x – 4))
That, of course, is what I got by first replacing x with 3x, and then replacing x in that with (x – 4).
And this is why everything involving horizontal transformations is backward: We’re really solving for the original x, which means undoing the operations, and doing that in reverse order.
In vertical transformations, like \(h(x) = 3f(x) + 4\), we are just evaluating an expression, and follow the order of operations: Multiply y by 3, then add 4; that is, stretch by a factor of 3, then shift up 4. But in the horizontal transformation, we are not evaluating but solving, which reverses everything.
So, to get back from our new x, 5, to the original x = 3, we first undo the shift right by 4, moving left by 4 to x = 1; and then we undo the shrink by 1/3, stretching by 3 from x = 1 to x = 3. That’s what puts the (x – 4) inside parentheses.
How does that work for you?
Transforming coordinates
Mario replied, restating my ideas in order to understand them better:
Interesting, I let this ruminate for a while, and I found what may be an alternate way of thinking about it.
You start with a function f(xf), and you want to find how to alter it in order to get to g(xg), using only horizontal transformations of course, and assuming g(xg) is only a horizontal transformation of f(xf).
However, we must do this under the constraint that the inputs of both of the functions are the same. In summary, we have to map f(xf) → g(xg) under the constraint of them having the same input. Currently, xf ≠ xg because the same input results in different outputs for f and g.
The way we would solve this is by considering the information that we have been given. We know that xg = ⅓ xf + 4. This equation is extracted from “horizontal shrink by ⅓” and “shift 4 spaces to the right”. If we solve for xf, we get xf = 3(xg – 4). We plug that into f, and we get f(3(xg – 4)) = g(xg). Notice that they both have xg as an input, satisfying our constraint.
What do you think of this way of thinking about it?
I answered:
I think that’s basically right, but needs a little clarification.
First, we can perhaps more clearly describe your “horizontal transformations” by saying that that xg is a linear function of xf.
Second, where you say,
However, we must do this under the constraint that the inputs of both of the functions are the same. In summary, we have to map f(xf) → g(xg) under the constraint of them having the same input. Currently, xf ≠ xg because the same input results in different outputs for f and g.
I don’t think you literally mean that the inputs (xf and xg) are the same; and I’m not sure how to say what you mean by a map of a function. I would express the idea by saying that f(xf) = g(xg) = g(T(xf)), where T is a linear transformation of the input variable, i.e. T(x) = ax + b. This makes it explicit how the functions are related.
The idea that we are transforming the variable, rather than the function, is a good perspective. You can imagine sliding and stretching the coordinate system itself while keeping the graph the same. In higher math this can be a valuable way to see coordinate transformations.
Inverting the transformation
Then you said,
The way we would solve this is by considering the information that we have been given. We know that xg = ⅓ xf + 4. This equation is extracted from “horizontal shrink by ⅓” and “shift 4 spaces to the right”. If we solve for xf, we get xf = 3(xg – 4). We plug that into f, and we get f(3(xg – 4)) = g(xg). Notice that they both have xg as an input, satisfying our constraint.
This nicely fits into what I just said. The example has T(x) = ⅓ x + 4, so that xg = T(xf) = ⅓ xf + 4. In solving, you are finding the inverse function, xf = T-1(xg) = 3(xg – 4).
Therefore, the requirement that f(xf) = g(T(xf)) implies that g(xg) = f(T-1(xg)) = f(3(xg – 4)).
If you’ve done enough with inverses in general, you may recognize that if T is a stretch/shrink A followed by a shift B, so that T(x) = B○A(x) = B(A(x)) = (⅓)x + 4, then the inverse is T-1(x) = A-1○B-1(x) = A-1(B-1(x)) = 3(x – 4), which fully explains the reversal of order. To undo a shrink followed by a shift, we have to undo the shift and then the shrink.
Does this express what you had in mind?
When you find the inverse of a composite function, it is equivalent to the composition of the individual inverses, in the reverse order. More generally, \((f\circ g)^{-1} = g^{-1}\circ f^{-1}\). (That is, if \(y=f(g(x))\), then \(x = g^{-1}(f^{-1}(y))\); so if \(h(x)=f(g(x))\), then \(h^{-1}(x) = g^{-1}(f^{-1}(x))\).) And this, in turn, is the same idea as when we solve equations, which I discussed in an early post, Why We Care About “Why”.
Mario agreed:
Yes, that is a better way of putting what I wanted to say. I agree, “f(xf) = g(xg) = g(T(xf)), where T is a linear transformation of the input variable” is a much better way of describing my idea rather than “map f(xf) → g(xg).”
With that, I was able to tell Mario,
I think I’ve said what I had in mind. Thanks for giving me the chance to say it!
