A common topic in algebra courses is how to transform functions and their graphs. In the series starting today, we’ll start with the basics of how and why a graph is moved or stretched, then combine transformations and look at various special cases and other transformations, ending up with graphing trigonometric functions.
Translating (shifting) a graph
Translation means moving an object without rotation, and can be described as “sliding”. In describing transformations of graphs, some textbooks use the formal term “translate”, while others use an informal term like “shift”.
Our first question comes from 1998:
Translating Functions Explain how the following graphs are obtained from the graph of y = f(x): y = f(x - 5) y = -f(x) y = f(5x)
These examples represent the three main transformations: translation (shifting), reflection (flipping), and dilation (stretching). I chose to focus on the first only, suggesting how the student could discover what a transformation does to the graph:
Here's how to think about it. Imagine you have just graphed a point of f(x), say at x = k:
|
| /
+ *
| /
|
----+------+-------
| k
Now you want to graph a point of f(x - 5) using what you just found out. Well, you know f(k). If x = k + 5, f(x-5) = f(k) which you just figured out. So the corresponding point in the new function to plot is x = k + 5, where it will have the same value:
|
| / /
+ * o
| / /
|
----+------+----+--
| k k+5
If you do this with every point in the graph, you will find that the graph of f(x - 5) is just the graph of f(x) slid to the right by 5. The other two cases are similar. Find what point of the new graph feeds the same value into f as the original, and what y is for the new function.
You may have seen this before if you had an equation like:
y = k*(x-a)^2 + b
and had to find the vertex of the parabola. Notice that this is just:
y = f(x-a) + b
where:
f(x) = k*x^2
whose vertex is at (0,0). So the vertex of the original equation is at (a,b). Knowing how transforming an equation transforms its graph is very useful.
Students often meet the standard form (vertex form) of the parabola before learning about transformations, so my example should be familiar; the vertex is (a, b) because the basic function is shifted a units to the right, and b units up. We’ll be seeing more of this soon.
Shifting and stretching
Here is another very similar question from 2001:
Graph with f(x) I am told to sketch the following equations, but do not know how to: y = f(x)+ 2 y = f(x-3) y = 2f(x)
This time we have a vertical translation, a horizontal translation, and a vertical dilation. I chose to illustrate each concept with sample graphs, with only brief explanation of why they do what they do:
Were you told what f(x) is? Without that, you can't really sketch the graph.
But if you were given just the graph of f(x), say some random squiggly line, you can graph these by seeing how they are related to f(x).
| __
| / \f(x)
| ___/ \
| / \___
|/
+---------------
g(x) = f(x)+2 is 2 units higher than f(x) for any x; so you just shift the graph upward 2 units:
__
| / \f(x)+2
| ___/ \
| / __ \___
|/ / \f(x) ^
| ___/ \ | 2 units
| / \___ |
|/
+---------------
h(x) = f(x-3) has the same value for a given value of x that f(x) has when x is 3 less. That is, the graph is shifted to the right three units, so that for example h(3) = f(3-3) = f(0).
| 3 units
| ------>
| __ __
| f(x)/ \ / \f(x-3)
| ___/ _\_/ \
| / / \___ \___
|/ /
+---------------
k(x) = 2f(x) is twice as high as f(x) at any given value of x; so you are stretching the graph vertically:
__
|
| / \2f(x)
|
| ___/ \
| __
| / / \ \___
| ___/ \
|// f(x)\___
|/
+---------------
Here are some actual graphs corresponding to the three above:
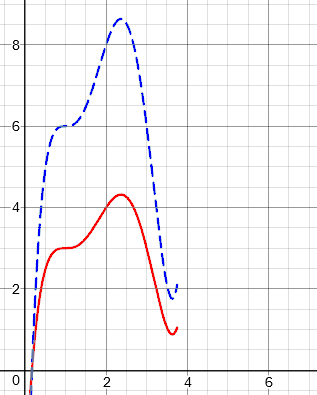
\(f(x)+2\) [shift up 2]: Here, the point (2, 4) moves to (2,6), adding 2 to the y.
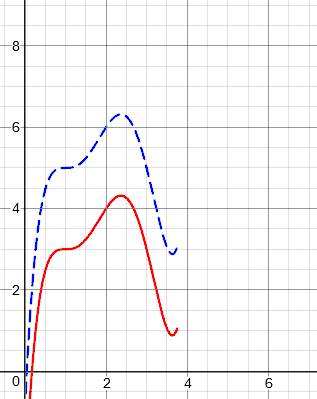
\(f(x-3)\) [shift right 3]: Here, the point (2, 4) moves to (5, 4), adding 3 to the x.
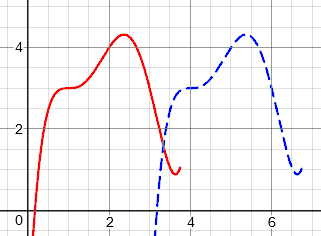
\(2f(x)\) [stretch vertically by a factor of 2]: Here, the point (2, 4) moves to (2, 8), doubling the y.
A note on reflection
None of these discussions went deeper into reflections than a brief mention in the first question. I will just add here that you can think of a reflection as a “stretch by a factor of \(-1\)”. That is, it just reverses direction. So a vertical reflection (reflection in the x-axis) is accomplished by \(-f(x)\), which changes the sign of y; and a horizontal reflection (reflection in the y-axis) is accomplished by \(f(-x)\), which changes the sign of x. These generally don’t give students any trouble, apart from remembering which is which. We’ll be seeing them again next time, because they do give trouble when we combine transformations.
Horizontal shifts: A closer look
The horizontal transformations, involving x, confuse many students. Here is a question from 2002 about just that:
Shifting Graphs Here's a passage I don't understand. "If g(x)=f(x-c), where c>0 then the value of g at x is the same as the value of f at x-c (c units to the left of x). Therefore, the graph of y=f(x-c) is just the graph of y=f(x) shifted c units to the right." I don't understand why it shifts to the right.
I referred to the last answer, and gave a little more detail:
Suppose you have just plotted a point (a,b) on the graph of y=f(x), and now you want to plot the same point on the graph of y=g(x). You have already calculated f(a) and got b, so you would like to reuse that information and save work. Since g(x) = f(x-c), you know that g(a+c) = f(a+c-c) = f(a) = b. So the point (a+c, b) will be on the new graph. This point is your original point (a,b) shifted c units to the right. The same will be true for every point on the graph of y=f(x), so the whole curve will be shifted c units to the right to make the graph of g.
We have to add c to x to compensate for the fact that it will be decreased by c before being fed into function f. So replacing \(x\) with \((x-c)\) in the function moves every point to the right by c units.
Horizontal stretches
In general, everything we do with x will be the opposite of what you might expect, for this same reason. This is true not only of horizontal shifts, but of horizontal stretching as well, which we haven’t seen yet. Here is a question specifically about that issue, from 2004:
Dilations of the Graph of y = f(x) Why is it that when doing a horizontal shrink or stretch you multiply by the reciprocal but when doing a vertical stretch or shrink you multiply by just the number? For example, to stretch y = f(x) vertically by a factor of 2 we just use y = 2*f(x), but to stretch it horizontally by a factor of 2 we use y = f(x/2). Why isn't it y = f(2x)?
Here is an example, based on our function above:
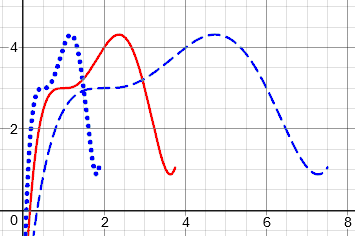
The dotted graph is f(2x), compressed (shrunk) by a factor of 1/2 horizontally; the point (2, 4) moves to (1, 4), halving the value of x.
The dashed graph is f(x/2), stretched by a factor of 2 horizontally; the point (2, 4) moves to (4, 4), doubling x.
I first looked at the more natural vertical transformations from a new perspective:
There's a different way to express the dilations (stretching and shrinking) that makes the two look more similar. As in your example, say we have an equation y = f(x) If you stretch the graph vertically by a factor of k, the new y will be k times what it was for a given x: y = k * f(x) But you can also think of it as replacing y in the original equation with y/k: y/k = f(x) That means that y for the new equation has to be k times as great as in the original equation, in order to be on the graph; dividing it by k gives you the equivalent "y" in the original equation, which is why we replace y with y/k to get the new equation.
The usual perspective multiplies the function value, obviously stretching it; here we are instead replacing y with y/k, forcing y to be k times as large.
Now let's stretch horizontally by a factor of k. That can be done by replacing x with x/k this time: y = f(x/k) When thought of in that way, the two approaches are the same--only the variable replaced changes depending on if you dilate vertically or horizontally.
We can do the same with translations, providing a different way to see the “oppositeness” of the horizontal stretch:
As an aside, a similar discussion holds for simple translations. The usual approach uses the notation: y = f(x - h) + k To move the graph 3 units right and 2 units up, we would have: y = f(x - 3) + 2 Again, students wonder why the upward shift of 2 is done with +2 while the shift to the right is done with -3. That doesn't seem consistent, either. But if we do the same thing and rewrite the equation as y - k = f(x - h) we can see that the two translations are in fact accomplished the same way.
This last form may look familiar to you; it is the same form as the “point-slope” form of a line.
In this view, any transformation is accomplished by replacing a variable with a new expression that does the opposite of the transformation.
Why horizontal transformations are backward
This general issue came up again in 2013:
Functional Transformations Explained and Undone Why do horizontal transformations behave in an opposite manner? For example, why does f(x + c) shift a graph c units to the left? Likewise, to shrink or stretch horizontally, i.e., f(cx), why do you divide the x coordinate by c?
I explained in terms of undoing:
Here's the idea. Suppose, for example, that the point (5, 6) is in the graph of y = f(x). This means that f(5) = 6. Now, consider the graph of g(x) = f(x + 4). Since we know that f(5) = 6, we know that g(1) = f(1 + 4) = 6. So the point (1, 6) is in the graph of g. This point is 4 units to the left of (5, 6). The same will be true of any point on the graph of g. Do you see what happened? In order to find the input to g that will correspond to 5 being the input to f, I had to SUBTRACT 4 from x -- that is, shift the point LEFT. In other words, when you replace x with x + c in a function, x must be c LESS that what it was in the original function in order to get the same output. Similarly, when you replace x with cx, x must be DIVIDED by c in order to get the same output.
What do you call it?
In 2014, we got a very different question, asking about the terminology of stretches:
Stretching Definitions, and Compressing The original function is y = f(x). Given a new function y = f(cx). Case (i) If 0 < c < 1, the graph is stretched horizontally by a factor of c units Case (ii) If c > 1, the graph is compressed horizontally by a factor of c units For case (i), why is the stretch factor not equal to 1/c? For case (ii), is the stretch factor c or 1/c? Do we always measure "stretch" in c units? and compress in 1/c units? I am really confused by this.
If you don’t see what Jason is concerned about, notice that for \(f\left(\frac{1}{2} x\right)\), his book calls it a stretch by a factor of \(\frac{1}{2}\), where I would call it 2; and it calls f(2x) a compression by a factor of 2, which could also be called a factor of \(\frac{1}{2}\) (since that is what coordinates are multiplied by). Is the book wrong?
I had observed that this terminology varies, and took the opportunity to research it a bit, breaking down what I found into cases:
I've seen this taught several ways -- which should tell you that it's really not important.
I(a). Some texts always use a factor greater than 1; they say that
f(2x) is compressed by a factor of 2
(meaning x is divided by 2)
f(x/2) is stretched by a factor of 2
(meaning x is multiplied by 2)
In general,
f(cx) is stretched by a factor of 1/c if 0 < c < 1,
and compressed by a factor of c if c > 1.
Here the "factor" cited is always greater than 1.
For example, see
http://blogformathematics.blogspot.com/2012/12/transformations-of-
functions.html
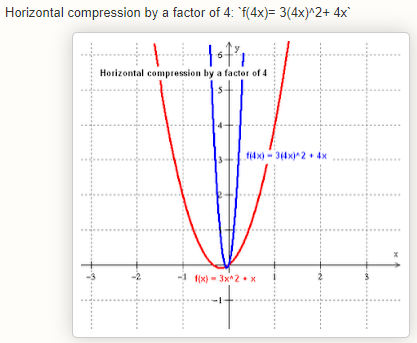 I(b). An alternative presentation of the rule is:
In general, taking c > 1,
f(cx) is compressed by a factor of c.
and f(x/c) is stretched by a factor of c.
See, for example,
http://archives.math.utk.edu/visual.calculus/0/functions.12/
I(b). An alternative presentation of the rule is:
In general, taking c > 1,
f(cx) is compressed by a factor of c.
and f(x/c) is stretched by a factor of c.
See, for example,
http://archives.math.utk.edu/visual.calculus/0/functions.12/
 II(a). Others say that
f(2x) is compressed by a factor of 1/2
(meaning x is multiplied by 1/2)
f(x/2) is stretched by a factor of 2
(meaning x is multiplied by 2)
In general,
f(cx) is stretched by a factor of 1/c if 0 < c < 1,
and compressed by a factor of 1/c if c > 1.
That is, x coordinates are multiplied by a factor of 1/c,
which is a stretch if 1/c > 1 and a compression if 0 < 1/c < 1.
For an example, see
http://math.kennesaw.edu/~sellerme/sfehtml/classes/math1113/
transformation.pdf
II(a). Others say that
f(2x) is compressed by a factor of 1/2
(meaning x is multiplied by 1/2)
f(x/2) is stretched by a factor of 2
(meaning x is multiplied by 2)
In general,
f(cx) is stretched by a factor of 1/c if 0 < c < 1,
and compressed by a factor of 1/c if c > 1.
That is, x coordinates are multiplied by a factor of 1/c,
which is a stretch if 1/c > 1 and a compression if 0 < 1/c < 1.
For an example, see
http://math.kennesaw.edu/~sellerme/sfehtml/classes/math1113/
transformation.pdf
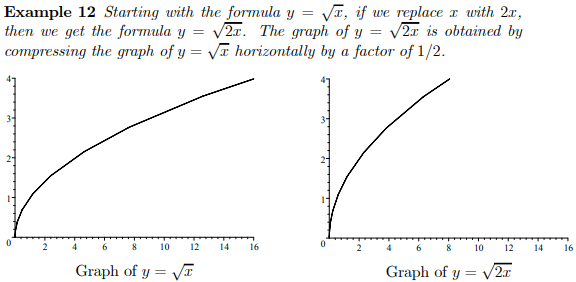 II(b). The following site seems to follow this approach, but in the horizontal case, they say the factor is c, not 1/c. They give no examples, so I don't know if they realize that they are saying f(x/2) is "stretched by a factor of 1/2," which makes no sense!
http://www.regentsprep.org/Regents/math/algtrig/ATP9/funclesson1.htm
II(b). The following site seems to follow this approach, but in the horizontal case, they say the factor is c, not 1/c. They give no examples, so I don't know if they realize that they are saying f(x/2) is "stretched by a factor of 1/2," which makes no sense!
http://www.regentsprep.org/Regents/math/algtrig/ATP9/funclesson1.htm
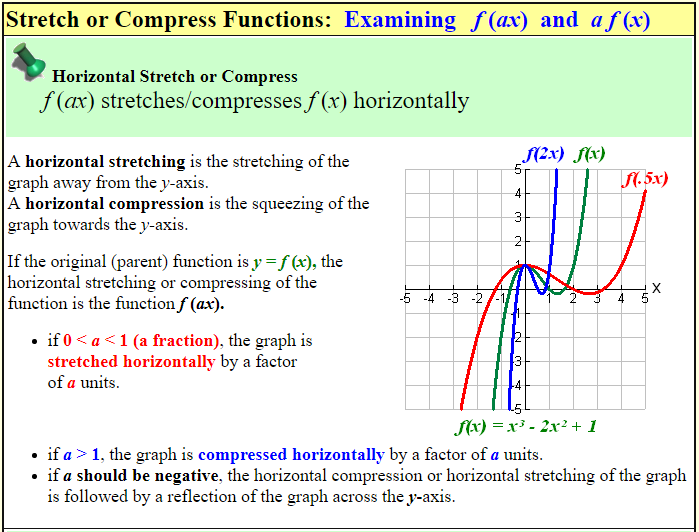 III. Yet others seem to avoid the terminology of "by a factor of c," and just say that
f(cx) divides x by c, which is a stretch if 0 < c < 1
and a compression if c > 1.
III. Yet others seem to avoid the terminology of "by a factor of c," and just say that
f(cx) divides x by c, which is a stretch if 0 < c < 1
and a compression if c > 1.
So, we find “compressed by a factor of 2” (I), and “compressed by a factor of 1/2” (II), meaning the same thing. As long as we focus more on the word than the number, we’re okay:
The first view (I) takes the word "stretch" or "compress" as telling you whether to multiply or divide, and makes the factor always greater than 1. The second view (II) takes the operation to be always multiplication, with stretching implying a factor greater than 1 and compressing implying a factor less than 1. I tend to prefer II(a), because "factor" implies multiplication, not division, and because it seems more natural to talk about compression as being by 1/2 rather than by 2. But I can appreciate the reasons for the other view, and I don't mark students wrong for expressing it that way. As long as they use the word "stretch" or "compress," I know what they mean; "compress by a factor of 2" can't mean multiplication by 2, so it must mean division by 2. The rules you quoted are the II(b) version, which as I noted is strange, and certainly not standard. I would not accept that usage from my students, because saying that the graph is stretched by a factor of 1/2 is incomprehensible, and I would not be sure they know what they are doing. You may want to adopt version III for your own thinking, as a way to avoid trouble in the future. But be aware that you will find all sorts of terminology in other sources, including future classes you take. Ultimately, you should do whatever your textbook and teacher say ... ... and hope that they agree: if not, the teacher must be aware of the issue and will either tell you not to worry about it, or make it clear what he expects.
Jason replied,
Dr. Peterson, thank you for your detailed explanation and the websites. I agree that II(a) makes more sense, and now have a better understanding of the concept.

Pingback: Combining Function Transformations: Order Matters – The Math Doctors
Pingback: Equivocal Function Transformations – The Math Doctors
Pingback: Finding Transformations from a Graph – The Math Doctors
Pingback: Translating a Curve: Multiple Methods – The Math Doctors
Thank you for doing all of this research on compression “by a factor of…”! I am grateful. It was exactly addressing an issue out of which I thought I would never make sense nor find any answers.
You’re welcome.
Before I did the research for that last question, I had a general sense of what was possible, but I was surprised by how much variation actually exists!
Pingback: Two Sinusoidal Models – The Math Doctors
Pingback: Exponential Growth: Surprisingly Flexible – The Math Doctors