Two recent questions from the same student involve exponential functions: We can express different kinds of growth all using one base, called e; or we can use different bases (and ignore horizontal scaling transformations). And we can use different transformation to obtain the same graph. This relates to some important properties of exponential functions.
Why can we always use ex?
The first question from Debarghya came in mid-May:
I have read following statement in a book:
Just like every number can be considered a scaled version of 1 (the base unit), every circle can be considered a scaled version of the unit circle (radius 1), and every rate of growth can be considered a scaled version of e (unit growth, perfectly compounded).
But e only comes for continuous growth where every part grows at the same rate. then how it can be considered as a unit for any growth? In fact how discrete growths like 2x, 3x etc can be related to e? e is related to many natural phenomena where growth is continuous. But is it fundamental for any growth even if the growth is discrete?
Checking now for the source, I find the quotation copied in many places, often without attribution, but it appears to originate in Better Explained (which also has a book). The preceding paragraph says,
e shows up whenever systems grow exponentially and continuously: population, radioactive decay, interest calculations, and more. Even jagged systems that don’t grow smoothly can be approximated by e.
The article then proceeds to work from repeated doubling, \(2^t\), and discrete compound interest, \(\left(1+\frac{r}{n}\right)^{nt}\) to the continuous case, \(e^{rt}\).
If you think about it, though, most exponential growth situations are really discrete, in that the number of people or atoms is actually a whole number. We just pretend they vary continuously to simplify things.
Doctor Fenton answered:
Growth rates such as 2x or 3x are discrete only if x is discrete. If x is continuous, then so are 2x and 3x. The general definition of an exponential ab is ab = eb ln(a), which will be a real value only if a > 0. For discrete compounding at regular intervals, such as at annual interest rate r with n compounding periods per year, the growth rate is (1 + r/n)n = en ln(1+r/n) .
Essentially, there is only one exponential function (i.e. a function with a constant base and variable exponent). (Similarly, there is essentially only one logarithm function, since by the change of base formula, logb(x) = loge(x)/loge(b) .)
The point is that all of these functions, whether \(2^x\) or \(\left(1+\frac{r}{n}\right)^n\), can be written as \(e^{kx}\); such a form can be used regardless of whether x takes only whole number values or not. What makes a problem discrete is merely that the independent variable happens to be only whole numbers; the formula is the same.
Debarghya replied,
What I understand from your reply is as follows:
Although by definition e results from continuous compounding but applying algebraic formula of logarithm properties we can apply e as base for any exponential and logarithmic function. But still my question is, how it can be considered as base unit like 1 in number system. It is true that we cannot take base 1 in exponential and logarithmic function. But why e is so fundamental or so basic? It is prevalent in many natural growth processes. So it is important to study. But how it can be unit growth?
One thought has come in my mind, since e corresponds to growth at every instant hence it can be considered as most basic growth. Because all other growths occur at certain intervals. hence e is most elementary growth for any growth processes. Is it the reason?
How, he is asking, can e be like a unit, as they claim, and fundamental to any exponential growth, when simple doubling seems to have so little to do with e?
After Doctor Fenton responded in a different direction, Debarghya clarified a little:
I understand that there are different rates of growth. e is involved with exponential growth where rate of growth is proportional to the base value. But I want to know that when we say 2x, 3x then they also mean exponential growth. but they are not continuous growth. If x is time then growth results after a certain time interval. But ex corresponds to continuous growth. isn’t it? So, occurrence of e other than any bases happen only when we consider continuous growth. Am I correct?
Here is my thinking:
All exponential growths are inherently continuous in nature. If we see it from grower’s perspective then every exponential growth can be modelled by base e. Here r is the rate of growth and t is the time interval after which final growth i.e., value of ert is observed. But from observer’s perspective any suitable measurement model can be obtained. He can take any suitable base. Is it correct explanation?
This is a good start!
Two perspectives on growth
Doctor Rick now answered:
Hi, Debarghya. I think your “two perspectives” approach is a good one. Here is my take on two perspectives:
From the application perspective, often there is one “natural” choice for the base of an exponential function, which depends on the application problem. For instance, for a “half-life” problem, base 1/2 is natural; for a “doubling time” problem, base 2 is natural; for a “growth rate” problem, we’d use (1 + r) as the base.
The application perspective is what’s natural for the problem (such as base 2 for doubling); the mathematical perspective will be what’s convenient for the solver.
But once we have chosen a mathematical model for the application problem, we’re in the realm of pure math. The property of exponents
(bk)x = bkx
allows us to write a power of any base as a power of another base, so we aren’t bound to our initial choice of base. For instance, I may have chosen a model
y = 2x
but I can rewrite it as
y = (10log 2)x = 10x log 2
if I prefer to work with a base of 10 (I don’t usually).
If we use base e, we get \(y=e^{x\ln2}\). It means the same thing.
Now, if I write
f(x) = 10x
then the function above is
y = f((log 2)x)
which you will recognize as a horizontal scaling of the parent function f. So once we choose one base to work with, every exponential function is a scaled version of f! That’s why the source you quoted said “every rate of growth can be considered a scaled version of e” (meaning ex). It’s a useful observation!
We discussed such scaling, for example, in Shifting and Stretching Graphs. (Scaling is equivalent to stretching or compressing.)
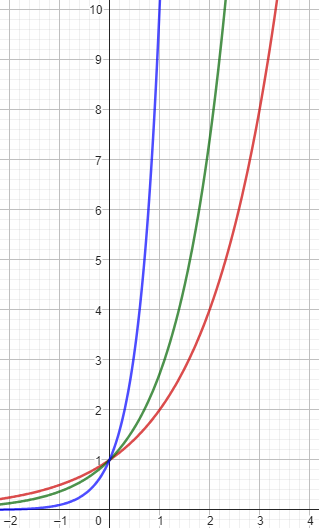
This is one way in which exponential functions are “flexible”: We can choose whatever base we like, and we are just changing the horizontal scale. Here are graphs of \({\color{Red}{2^x}},{\color{DarkGreen}{e^x}},{\color{Blue}{10^x}}\):
Why is e like a unit?
Now, from the mathematical perspective, why would we prefer to work with e as our standard base? The primary reason comes from calculus — just as calculus provides the strongest reason for using radian measure with trigonometric functions.
The derivative of sin x is very simple (namely cos x) if we choose a scaling for x that makes sin x have period 2π (in other words, if we work in radians). If we worked with degrees, the derivative of sin x would be π/180 cos x.
Likewise, the derivative of ex is very simple (it’s ex again!) but if we choose something other than e as our base, then we’ll need an extra factor.
I don’t know whether you have even heard of a derivative yet. It is the rate of change of a function (the ratio of a change in y to a change in x; or, the slope of the graph at a point). In an exponential function, the rate of change is proportional to the value of the function itself; in the case of f(x) = ex, the constant of proportionality is 1. That’s the sense in which e can be compared to the number 1.
The point is that once you learn calculus, you’ll be very glad we use e (and \(\pi\))! And to answer the central question, once we discover the centrality of e for continuous growth, we read it back into discrete growth to keep the math consistent.
What point is the image of (0, 1)?
Debarghya had a new question two weeks later:
I was trying to solve problems regarding how to find equations of exponential function from graph. I could solve problems in the form of y = abx+c. I just need to find shifting of asymptotes w.r.t. parent function bx to get c. then from any two points on graph we could solve two equations to get a and b.
But I was unable to get equations from graph involving vertical stretching or horizontal shifting. I got this tutorial where a method has been discussed.
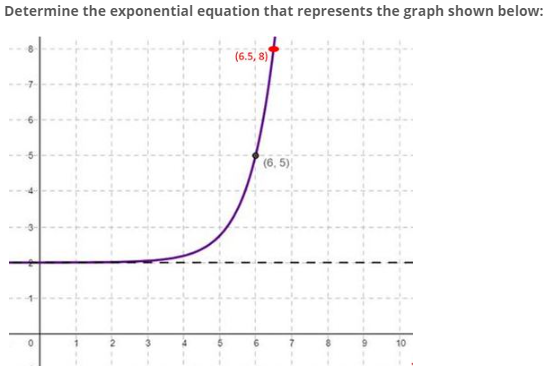
In the first example at step 2 a conclusion has been made as follows:
“The point (6, 5) labeled on the graph corresponds to the point (0, 1) normally located on the simplest exponential function”.
It makes easier to find c. but how could we know that (6,5) is the image point of (0,1)? or, is it implicit that point marked on graph are image point of (0,1). That definitely solves the problem. But without having any idea of image point of (0, 1) how could we found the horizontal shift? Please help.
Here is that first example:
Using two points to write equations for the parameters, as he initially says (and as we’ll do later), is a standard method; this author, instead, seems to assume we know what point is the image of the standard point \((0,1)\) on the parent graph. But how do they know that? (Spoiler: They don’t need to.)
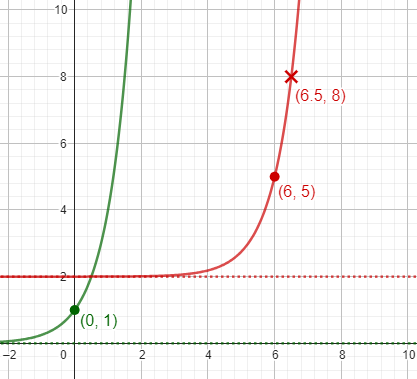
Here are the parent and given graphs (though we don’t yet know what the base of the parent is):
In summary, what they do is to find the parameters a, b, c, and d in \(y=a\cdot b^{x-c}+d\), by
- first finding the vertical shift, \(d=2\) from the asymptote, \(y=2\); then
- finding the horizontal shift, \(c=6\), that moves \((0,1)\) to \((6,?)\); then
- finding the vertical stretch, \(a=3\), from the distance of \((6,5)\) above the asymptote; and, finally,
- finding the base, using the other point, \((6.5,8)\): \(3\cdot b^{6.5-6}+2=8\;\Rightarrow\;b^{0.5}=2\;\Rightarrow\;b=4\).
The result is \(y=3(4)^{x-6}+2\).
Doctor Rick answered:
Hi, Debarghya.
You ask,
But how could we know that (6,5) is the image point of (0,1)?
I’d like you to try something. Suppose we switch the roles of the two points shown on the graph. That is, let the point (6.5, 8) correspond to (0, 1) on the parent function, and use (6, 5) later. What exponential function do you end up with? How does it compare with the function obtained in the example, y = 3(4)x–6 + 2?
We commonly answer questions like “Why must I do this instead of that?” by saying, “Try doing that, and see what happens”. That’s a good way to think of what he asked: “What if we used the other point instead?” Sometimes, the answer turns out to be, “It doesn’t matter which way you do it!”
Different point, different equation … same graph!
Debarghya replied,
I got the equation
y = 6(4)x–6.5 + 2
and this results in same graph!
But why this happens? If I consider any point as image of (0,1) and then I plug in any other point then how that results in same graph?
Here is the work, using the same method with the alternative assumption:
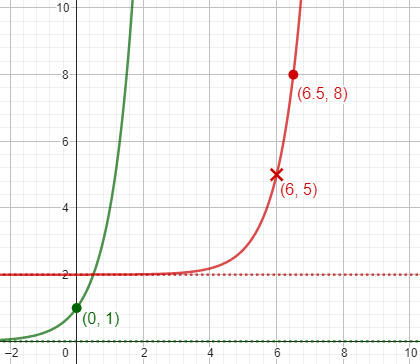
- Find the vertical shift, \(d=2\) from the asymptote, \(y=2\).
- Find the horizontal shift, \(c=6.5\), that moves \((0,1)\) to \((6.5,?)\).
- Find the vertical stretch, \(a=6\), from the distance of \((6.5,8)\) above the asymptote.
- Find the base, using the other point, \((6,5)\): \(6\cdot b^{6-6.5}+2=5\;\Rightarrow\;b^{-0.5}=\frac{1}{2}\;\Rightarrow\;b=4\).
The result is \(y=6(4)^{x-6.5}+2\). Its graph is the same as \(y=3(4)^{x-6}+2\). Why? Simplify each equation:
$$3(4)^{x-6}+2=3\cdot\frac{4^x}{4^6}+2$$ $$6(4)^{x-6.5}+2=6\cdot\frac{4^x}{4^{6.5}}+2=6\cdot\frac{4^x}{2\cdot4^6}+2=3\cdot\frac{4^x}{4^6}+2$$
They are the same function.
Doctor Rick responded:
It’s interesting, isn’t it? Rather unexpected …
We’re talking about a family of functions of the form
f(x) = a·bx–h + k
where h and k are the horizontal and vertical shifts and a is the vertical scale factor. Before I go on, what happened to the horizontal scale factor? It would be better to use a fixed base, let’s say e (I think we talked a little about this). That is, our parent function is f(x) = ex. Then we could write the family as
g(x) = af(c(x–h)) + k = a·ec(x–h) + k
Now you can see the horizontal scale factor c; in fact, c = ln b.
The author’s form, \(f(x)=a\cdot b^{x-c}+k\), doesn’t need a horizontal scale factor because changing the base has the same effect. There’s more, however:
But the exponential function has a special property that connects the horizontal shift and vertical scale:
ex–h = ex / eh = (1/eh)ex
Thus a horizontal shift of h has the same effect as vertical scaling by eh. We don’t need both of these transformations; either one alone will do. Let’s choose to drop the horizontal shift, so that our family is reduced to
g(x) = a·ecx + k, or
g(x) = a·bx + k
if you prefer. Either way, there are only three free parameters (a, c, and k; or a, b, and k) defining a given exponential curve, not four.
So the author’s horizontal shift was unnecessary! Above, we rewrote our example without a shift as $$y=\frac{3}{4^6}4^x+2=\frac{3}{4096}4^x+2$$ But they needed the horizontal shift for their method, in order to move the given point to \(x=0\).
In this form, we could have started with \(y=a\cdot b^x + 2\), knowing that the vertical shift is 2, and, just as Debarghya said at the start, plug in the two given points to obtain the two equations $$a\cdot b^6 + 2=5\\\\a\cdot b^{6.5} + 2=8$$ These can be solved by simplifying each, then dividing to eliminate a: $$a\cdot b^6=3\\\\a\cdot b^{6.5}=6$$ $$\frac{b^{6.5}}{b^6}=\frac{6}{3}$$ $$b^{0.5}=2$$ $$b=4$$
Then the first equation can be solved for a: $$a\cdot 4^6=3\\\\a=\frac{3}{4^6}$$
Returning to the author’s method:
The method you were reading for determining the equation of an exponential graph had us choose a point on the graph to correspond to the point (0, 1) on the parent function y = ex. It didn’t make clear that any point on the curve will do. After we’ve dealt with the vertical shift by moving the horizontal asymptote to the x axis, we’re just talking about equations of the form
g(x) = a·bx
Any two points will determine the values of the two free parameters. Suppose the points (x1, y1) and (x2, y2) are on the curve; that means
a·bx1 = y1 [1]
a·bx2 = y2 [2]
I think this is worth your discovering it for yourself. How can you solve the system of equations [1] and [2], in general? Hint: you’d like to eliminate one of the variables a and b; there is a nice way to eliminate a.
What he describes is what we just did for the specific example.
Debarghya replied:
What I understood are as follows:
- c = ln b. this means ec=b. it means that horizontal scaling of c has same effect as that of using base b without horizontal scaling.
- Horizontal shifting of h has the same effect as vertical scaling by eh. If our parent function has vertical scaling 1 then we could use either horizontal shifting of h or vertical scaling eh.
So, our choice becomes c or b and h or a. isn’t it?
So, any transformed exponential function is essentially of the form (abx+k). nothing else. am I right?
Now, coming back to your question, if we divide equation 1 by 2 then a will be eliminated. I can solve the rest part.
The equivalence of horizontal shift and vertical scaling is similar to issues discussed in Equivocal Function Transformations, for squaring, square roots, and logarithms.
An explicit formula shows symmetry
Doctor Rick approved, and proposed finding a general formula:
Your understanding is correct.
You are correct also about how to solve the system of equations. What does that give you as a general formula for the exponential equation (with the x axis as asymptote) whose graph contains the points (x1, y1) and (x2, y2)? In particular, what are a and b in the equation y = a·bx, in terms of x1, y1, x2, and y2?
We started by talking about two methods for solving a specific problem; a general formula will make it more complicated, but will also reveal how the points are interchangeable.
Debarghya answered:
a = y1-p y2q
here p = (x2)/(x2-x1) and q = (x1)/(x1-x2)
b = (y1 / y2)1/(x2–x1)
Doctor Rick responded:
Good! I was interested to see how you could handle solving equations with variables (parameters) instead of numbers, and you did well. I might have stopped with
b = (y1 / y2)1/(x2–x1)
a = y1 / bx1
but you went further; in that case, we could make the formula for “a” a bit more symmetrical like this:
a = y1p y2q
where p = x2/(x2–x1) and q = x1/(x1–x2)
but the only reason I have for doing this is that it makes it a little easier to see that if we swap the two points (interchanging subscripts 1 and 2), we get the same result. Remember how we got to this point? You discovered that it didn’t matter which of two points you took as the “base point”, you’d get the same equation either way. The symmetry under interchange of subscripts 1 and 2 in the formula is directly related to your observation.
Here is the formula all put together, including the vertical shift k: $$y=\left(y_1-k\right)^{\frac{x_2}{x_2-x_1}} \left(y_2-k\right)^{\frac{x_1}{x_1-x_2}} \left(\frac{y_2-k}{y_1-k}\right)^\frac{x}{x_2-x_1}+k$$
