Is Zero Really a Number?

A recent comment on the site raised questions about zero, beyond what we have discussed in the past about division by zero. Here we’ll look at basic questions about whether zero is actually a number at all, and then about multiplication by zero, which confuses a lot of people.

Infinity isn’t a number; why is zero?

We’ll start with a question from 2003:

Is Zero a Number?

If infinity is not a number, then is zero really a number?  I see that it is not recognized as a real number but as a whole number, integer, etc. It seems as though zero has been accepted as a number and infinity has been accepted as a concept. This question stems from an argument about 1/0 = infinity.

As explained in Why Can’t You Divide by Zero?, where we discuss 1/0, infinity is not a number because it doesn’t follow the rules of numbers. Zero, too, behaves a little oddly; is it, too, not a number?

Doctor Jaffee answered:

Hi Joe,

Zero is a number; in fact, it is a real number.  It is on the number line right between 1 and -1. You can add, subtract, and multiply with 0 and get real answers. You can divide numbers into zero and get a real answer, zero.

You can't say anything like that about infinity.  It is not on the number line and you can't do computations with it.

It isn’t clear why Joe thinks zero is called a whole number, but not a real number. He probably misread something.

What follows is a brief summary of some of the ideas discussed in the post about division by zero.

Now, consider 1/0. You know that 1/1 =1, 1/0.1 = 10, 1/0.01 = 100,1/0.001 = 1000, etc... Pick a power of 10 as large as you want and I can find a number larger than 0 that I can divide into 1 and get your number as a result.

In other words, as we divide numbers into 1 and those numbers get closer and closer to 0, the quotient gets larger and larger with no boundary. We conclude then, that 1/0 = infinity.

However, that is just a shorthand notation.  Actually, division by zero is undefined.  It is more precise to say that

  Limit 1/x = oo    As x gets closer to zero, the value of 1/x
   x->0             grows without bound (i.e., approaches infinity)

Unfortunately, often people will use the shorthand, without making it clear that this is what's going on.  So other people see what they've written, and think that '1/0 = infinity' is an actual statement of fact, when it's not. 

In the same way, people will often write '1/infinity = 0', instead of the more precise

  Limit 1/x = 0     As x grows without bound (i.e., approaches
   x->oo            infinity), the value of 1/x gets closer to 0. 

But '1/infinity = 0' is also untrue.

This may be part of what Joe had in mind: that zero is closely tied to infinity, so if one is undefined, the other must be, as well. But the fact that we can get zero in an illegitimate way from an undefined “number” does not mean it does not exist on its own!

Is zero, like infinity, just a concept?

This same idea was taken deeper by Swapnil in 2005:

Is Zero Really a Number or Just a Concept?

Hi, for a long time my teachers have hammered into my brain that infinity is not a number, it's just a concept.  Now that I understand that, I wonder if zero is just a concept too?  I guess this is both a philosophical and a mathematical question. 

Philosophically, you can't really have a zero of things, because the thing which is zero doesn't really exist.  In fact, if you do count things that don't really exist, you will have an infinite number of those things since there is no limit to things that you can imagine existing (which is rather an interesting fact).

In mathematics, many definitions and rules go haywire when they try to deal with zero (such as 0^0, 1/0, 0/0).  The two most used bounds for evaluating the limit of a function are in fact 0 and infinity.

So it seems obvious that there is a deep intricate relation between zero and infinity.  And like infinity, it seems that zero should just be considered a concept.  Furthermore, by making zero a concept we would be able to avoid writing those exceptions to rules where we have to specify that the equation is true as long as something is not zero. 

I just thought of few more examples:

1) If in a game, your opponent has 1 point and you have two points then you can say that you have twice as many points as him.  Whereas if your opponent has zero points and you have two points, you would technically have to say that you have infinite times as many points as him.
2) You can't really have a circle with radius zero.
3) Zero is neither positive nor negative.

His idea of not having “a zero of things” seems to relate to the idea, discussed in Empty Sets and Vacuous Truth, that “the set of all elephants in Antarctica and the set of all living Tyrannosaurs are the same set.” Given an empty set, you can’t tell what sort of “thing” it [doesn’t] contain! The oddities of an empty set relate closely to the oddities of zero, which support his idea that zero is too peculiar to be called a number.

I answered:

Hi, Swapnil.

It's true that infinity and zero have many interesting relationships. But zero is far less troublesome than infinity, and far more important.  We couldn't do much algebra without zero, because we couldn't define the additive inverse (negative) without the additive identity.  For example, in solving x+5 = 1, we add -5 to each side, getting x+5-5 = 1-5.  The left side becomes x because 5-5 = 0, and x+0 = x.  We couldn't do that without zero! There would be ways to get around it, I suppose, but they would be very awkward.  You'd lose a lot if you refused to do any arithmetic with zero, which is what we mean when we say that infinity is not a number.

Zero is central to what numbers are, really. We can’t do arithmetic with infinity, but we must do arithmetic with zero!

(There was a time when 0 was not considered a number; in fact, at that time 1 wasn’t considered a number either – because it is not plural! But including both made mathematics far more coherent. See A history of Zero, 2020 and the Y0K Problem, and Is One A Number?)

Now, it's true that zero is "just a concept"--but the same can be said of all numbers.  You've never seen a three, have you?  You see three boys, three sticks, and so on, and you generalize from that to the concept of "three".

You can't have zero apples--but you also can't have -3 apples.  (Actually, you can have both, if you think of it the right way.)  You can't have a circle with radius 0, or with radius -3, either--so do negative numbers not exist?  Zero and negative numbers are just extensions of the concept of counting, taking the idea of "number" beyond where it began.

You actually can, of course, have zero apples (that’s how many are in my hand as I type this!). And you can have a negative number of apples if you owe them. This is discussed in How Real Are Negative Numbers?

The reason zero is neither positive nor negative is that positive MEANS greater than zero, and negative means less than zero.  Zero is not an exception there--it's what the whole idea of positive and negative revolves around (almost literally!).

We’ll discuss this more next time.

In general, zero works in MOST settings, while infinity works in almost none of them.  You can't divide by zero, but you can add it; you can't even add infinity without getting in trouble!  So it makes good sense to work with the few peculiarities of zero, but to treat infinity as something else, just a direction to go when you take a limit, rather than an actual destination.

Zero is the starting point on which numbers are built, which makes it special, infinity is sort of an ending point (that you can’t actually get to), which puts it outside.

Multiplying by zero: Money

A common confusion about zero is how you can multiply by it and get “nothing”. We’ll look at four such questions, starting with this from 2001:

Multiplying by 0

This may be a stupid question, but why, when multiplying any number by 0, do you get 0? 

If I have a dollar in my hand and multiply it by 0, won't I still have a dollar? If not, then who took my dollar?

This is a common thought: If zero means nothing, then multiplying by it should do nothing, right?

Is it this,

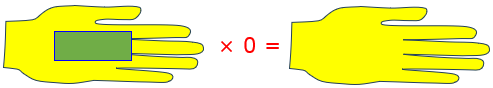
or this?

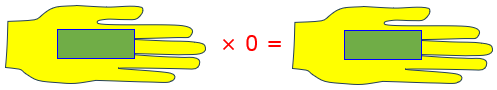
(Incidentally, in all my pictures I will be using \(a\times b\) to represent a being multiplied by b, so the second operand is taken as the number of repetitions (the multiplier). If you question this, see What is Multiplication? Multiplicand and Multiplier.)

Doctor Rick answered first:

Hi, Bruce.

They say the only stupid question is the one that you don't ask. Even "stupid questions" can lead to interesting insights if they make us look at the obvious in a new way. I don't know if I'll do that, but it could happen!

What does your illustration mean? If I have a dollar and multiply it by 2, I have $2. I could just as well ask where the second dollar came from, as you can ask where your dollar went.

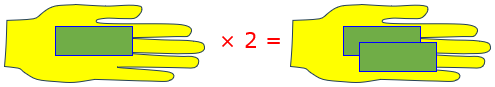
In this image of multiplication, it seems to be a magic wand that can create money from nothing.

But in reality, the $1 was not in your hand in the first place:

Let's fix your picture to make it clear where money is coming from. Let's say you're a barber and every customer tips you a dollar. At the end of the day, how much have you made in tips? Multiply a dollar by the number of customers you had. If you had 10 customers, you made $10. If you had 20 customers, you made $20.

So, what about the day that your shop was closed because of a blizzard? By your reasoning, you'd still make a buck, even though you had zero customers. 

No, it's clear that you make $0: $1 times 0 customers is $0.

Multiplication can be modeled in several ways; here we see it, in effect, as repeated addition.

Multiply $1 per customer by 2 customers, and there are $2 in the tip jar:

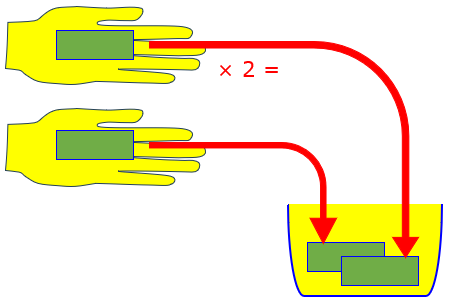
No customers, no money!

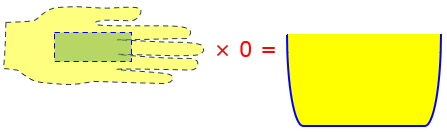
Adding together no things produces nothing.

A few minutes later, I answered with a sort of reversed image:

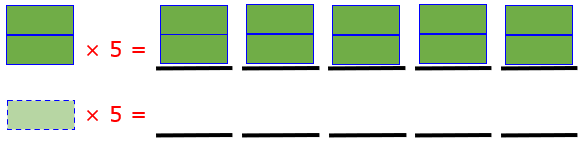
Hi, Bruce.

Picture multiplication by a whole number as making that many piles, each containing the original amount. If I start with a dollar and multiply by 5, I make 5 piles with a dollar in each. If I multiply by zero instead, I have zero piles; and zero piles (no matter how much I claim "each of them" has) will contain zero dollars.

Rather than 5 customers each paying a dollar, we now have one person making 5 piles. This doesn’t trace the origin of the money, but still has the idea that it comes from somewhere. It is not transmuting in the hand, but is moving.

Here are 5 piles of 1 (\(1\times5=5\)), and 0 piles of 1 (\(1\times0=0\)):

The $1 is not an amount we start with; it’s just an instruction we give, for the number in each pile.

But we can also see it reversed in another way:

You can also go in the other direction, multiplying zero by anything; this should give the same result. So start with 0 dollars, and make 57 piles, each containing zero dollars. Again, the total is zero.

Here are 5 piles of 2 (\(2\times5=10\)), and 5 piles of 0 (\(0\times5=0\)):

I'm wondering if you are confusing "multiplying by 0" with "adding zero times as much." If you have a dollar in your hand and multiply it by ONE, you will still have the same amount; multiplying by one doesn't change anything. Multiplying by 2 takes what you had, makes another copy of it, and gives you back twice what you started with. But multiplying by zero takes away what you had and gives you none of it back.

We say that 1 is the multiplicative identity: It leaves the amount unchanged. Zero is the additive identity: Adding zero leaves the amount unchanged. Multiplying by zero is different!

Multiplying by zero: Steps

Again, from 2002:

Multiplying by Zero

Dear Dr. Math, 

I know that zero's value is nothing, but why is it that it turns other numbers that clearly have a greater value to zero when multiplied? I have tried to answer that question in my research so far but I have been unsuccessful.

Doctor Ian answered:

Hi Carley,

If I understand your question correctly, you want to know why, if you multiply zero by _anything_, no matter how big, you get zero as a product:
 
                              1 * 0 = 0

                             27 * 0 = 0
 
  1,887,457,234,543,243,113,946 * 0 = 0

When you multiply one number by another, you can think of starting at some point ('the spot marked X', or wherever) and moving some distance away from it. To move, you need to know two things:

  1) how many steps you're going to take

  2) how big each step will be

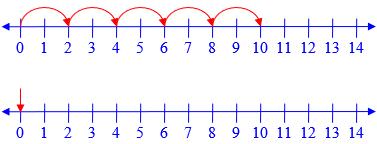
Now, if each step is of zero size, then you can keep taking them, and you'll never move anywhere. (Move a step of length zero. You're still where you started. Do it again. Still there. Keep doing it... how many of those steps will you have to take to actually move somewhere?) So any number times zero is still zero.

(He is using the “times” formulation, where \(27\times0\) means repeating 0, 27 times, with the first  number being the multiplicand; I will continue writing it as \(0\times27=0\), meaning 0 multiplied by 27, for consistency.)

Here are 5 steps of size 2 (\(2\times5=10\)), and 5 steps of size 0 (\(0\times5=0\)):

Now he does the same with 0 as the multiplier:

Also, if you're not going to take any steps, it doesn't matter how large a step you _would_ take, since you're not going to take it. So zero times any number is still zero.

Here are 2 steps of size 5 (\(5\times2=10\)), and 0 steps of size 5 (\(5\times0=0\)):

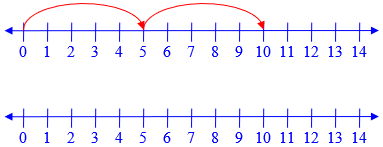
No steps, no movement!

Multiplying by zero: Algebra

Earlier in 2002, we got this question:

Multiplying by Zero

I was going through your website (which is wonderful by the way!) and I noticed some proofs that were really interesting about (-1)(-1) = +1 and so on. So I sat and thought about something like Mx0, and for the life of me I couldn't figure it out. We have been told since we were in 4th grade to learn it and accept it as truth, but now I am really curious as to how it is true. I was wondering if you could help me out. Thanks a lot!

Those proofs of negative times negative are found in Negative x Negative = Positive? Abstract Proofs.

Doctor Rick answered:

Hi, Jess.

I'm glad you like our site. Are you asking for a proof that any number times zero is zero? It's good to go back to basics such as this sometimes, as you suggest. When you learned the basics, you weren't as critical and logical as you are now, so they couldn't be presented in a way that would satisfy you now. But they can be, now that you're ready.

Pictures, like our answers above, can help in understanding at lower levels; but now we can use algebra.

We start out with just the counting numbers 1, 2, 3, ... . We find that the operations on these numbers have properties: commutative, associative, distributive, and so on. When we add zero to the number system, we want the same properties to continue to hold. Here is what we discover as a result:

  1 = 1 + 0       (0 is defined as additive identity)

  M*1 = M(1 + 0)  (property of equality: equals times equals are equal)
      = M*1 + M*0 (distributive property)

I won't bother to evaluate M*1 = M, because this isn't needed for the proof. I just subtract M*1 from each side:

  0 = M*0         (equals minus equals are equal)

That's what we wanted to prove. Does this answer your question?

So the fact that zero is the additive identity, and a couple other facts, require us to conclude that zero times anything is zero.

Multiplying by zero: More algebra

We’ll close with a question from 2003:

Algebraic Proof That a*0 = 0

If "a" is any element of all real numbers, then a*0 = 0.  I would like to understand the specific theorem or proof behind this idea.

Doctor Rob answered, with a fuller version of the same proof:

Thanks for writing to Ask Dr. Math, Katie!

The basic property of 0 is that, for any real number b,

   0 + b = b.

In particular, if b = 1,

   0 + 1 = 1.

Now multiply both sides by any real number a.  Then

   a*(0 + 1) = a*1.

Now recall that a*1 = a, by the definition of 1.  Apply the Distributive Law to the left side:

   a*0 + a*1 = a*1,
   a*0 + a = a.

Now add the negative of a to both sides:

   (a*0 + a) + (-a) = a + (-a).

Use the Associative Law of Addition on the left side:

   a*0 + (a + (-a)) = a + (-a).

Now use the fact that a number plus its negative is 0, which is the definition of the negative of a real number, so a + (-a) = 0:

   a*0 + (a + (-a)) = a + (-a),
   a*0 + 0 = 0,
   a*0 = 0.

Here he used the fact that 1 is the multiplicative identity (which wasn’t really needed), and justified the subtraction step using the additive inverse.