How Real Are Negative Numbers?

This week we’ll look at some Ask Dr. Math questions like, “How can a number be less than zero?” and “Why do we need negative numbers?” We’ll see a number of examples of their use, and how negative numbers make life easier.

Can’t (always) do it!

First, we have a question from 1998, from a child who didn’t yet know about negative numbers:

Introduction to Negative Numbers

Dear Dr. Math,

I want to know what does 11 - 12 equal?

Sincerely,
Jacob

I answered:

Hi, Jacob. 

That's a good question. It's easy to say what 12 - 11 is, so shouldn't 11 - 12 have an answer too?

Until recently, my own 6-year-old daughter would have written 11 - 12 = C, which stood for "Can't do it."

For some questions, that's the best answer you can give. Suppose you had 11 carrots on your dinner plate, and because I love carrots so much, while your head is turned I try to take 12 carrots from your plate. I can't do it!

My daughter is now working in a school (but not teaching math)! She invented this notation for herself; then I explained negative numbers to her.

Sometimes only positive numbers make sense, and for some problems “no solution” is the correct answer. But sometimes we can get past this barrier:

But suppose you had 11 dollars in your bank, and you wanted to buy a game that costs 12 dollars. You can't do it, but I might be kind enough to lend you a dollar. Then you would spend all 11 of your dollars, and you would owe me another dollar. You would actually have one dollar less than nothing, because as soon as you earned another dollar, it would go to me and you would have nothing!

We’ve put an IOU in the bank:

This will “cancel out” the next dollar put into it:

For a similar way to think about “negative apples”, see Picturing Negative Numbers.

Several hundred years ago mathematicians realized that there were a lot of problems they could solve if they had a way to talk about numbers less than zero. So they decided to write 0 - 1 = -1, which is read as "negative one" and means "one less than zero." From what I just said about owing a dollar, you can see that:

   11 - 12 = -1 (when you spend 12 dollars, you owe me one)

and

   -1 + 1 = 0   (when you earn another dollar, you will have nothing)

This idea actually arose before the modern use of symbols; they would have written \(-1\) as “m.1”. The point is that they had a concept of negative numbers.

There's actually another place where you can see negative numbers very easily. Look on a thermometer, and you'll see that the temperature can go down to zero degrees, but then it can keep getting lower. Temperatures below zero are written as negative numbers, like 

   -10 degrees

which means 10 degrees below zero. If the temperature now is 11 degrees, and it gets 12 degrees colder, it will be -1 degrees.

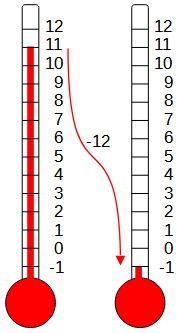
We’ll see this example a lot; rather than counting negative objects, we are measuring positions along a line that goes in both directions, which makes more sense.

Avoiding special cases

Next, from teacher Mary Ellen in 1999:

Using Integers

I need real-life examples of integers to show my 7th grade students, to demonstrate the fact that they need to be able to use them in math class. I've mentioned scores in some games, yardage in football, and the balance page of an accountant's book. Can you give me some more? Thanks.

Doctor Rick answered this:

Hi, Mary Ellen, welcome to Ask Dr. Math!

I presume you're talking in particular about places where we use numbers that may be either positive or negative, and it's really helpful to be able to treat them as the same kind of number, instead of needing a separate rule for each combination of negative and positive numbers. Some examples aren't really integers but positive or negative real numbers.

We’ve seen a lot of people confuse the concepts of “integer” and “signed number”, presumably because of the way they are often introduced together in school. Integers can be positive or negative, but the primary meaning of the word is “whole“: They don’t include fractions. But even fractions can have signs. For more, see What is an Integer?

How about temperatures? Conversion between Fahrenheit and Celsius on a sub-freezing day is a good exercise in using negative numbers.

Elevations go negative in places like Death Valley and the Dead Sea. Comparing the base-to-peak heights of Mount Everest and Mauna Loa is an exercise in subtracting negative numbers.

Latitude and longitude are easier to work with if you take east/north as positive and west/south as negative. The most obviously useful calculation here is in working with time zones - you'll find charts with time zones labeled EST = -5, Eastern Europe = +2, etc.

All of these are measurements along a line, up and down or left and right.

Years are a peculiar case. AD and BC were invented around AD 525, before negative numbers (or zero) were really understood, so there was no year zero. The year after 1 BC was AD 1. If it had been done right, we would have been able to compute the years between 43 BC and 33 AD as 33 - (-43) = 76. But because dates aren't integers, you have to say 33 + 43 - 1 = 75. In other words, when the calendar was devised, people just accepted the need for special cases, but with the invention of integers, we found a better way.

For a fuller discussion of this, see 2020 and the Y0K Problem.

By the way, the federal government does not assume that taxpayers understand integers, so the 1040 form uses the special-case approach: "If line 64 is LESS than line 59, subtract line 64 from line 59 and write it in line 65. If line 64 is GREATER than line 59, subtract line 59 from line 64 and write it in line 66." (That's the idea anyway, I got my form yesterday but I don't have it in front of me.)

Here is an actual example:

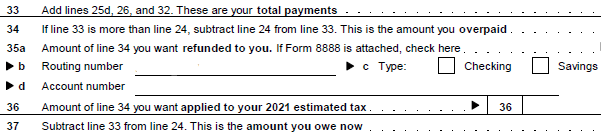
On line 34 a positive number is an overpayment, while on line 37 a positive number is an underpayment. In each case, a positive amount of money has to be transferred.

This is probably a wise decision on the part of the Internal Revenue Service, since many people would make mistakes with negative numbers.

I can't think of any everyday cases where we multiply negatives by negatives. But when your students learn about quadratic equations, they will be benefiting again from the no-special-cases property of integers. Early developers of algebra had to present solutions for 6 kinds of quadratic equations:

  http://www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/Al-Khwarizmi.html

Your students will learn a one-size-fits-all solution method.

The link says:

He first reduces an equation (linear or quadratic) to one of six standard forms:

1. Squares equal to roots [e.g. \(x^2=10x\)].
2. Squares equal to numbers [e.g. \(x^2=16\)].
3. Roots equal to numbers [e.g. \(x=10\)].
4. Squares and roots equal to numbers; e.g. \(x^{2}+10x=39\).
5. Squares and numbers equal to roots; e.g. \(x^{2}+21=10x\).
6. Roots and numbers equal to squares; e.g. \(3x+4=x^{2}\).

Don’t let the IRS get its hands on the quadratic formula!

Equations and coordinates

This is from 2002:

Practical Applications of Negative Numbers

I am preparing a unit on operations with negative numbers for a class of very bright and accelerated fifth graders. I would like them to have some of the theory and background on negative numbers other than the obvious temperature and checkbook examples. What is the history of negatives? Why were they invented, considering that you can't have -2 of a given object? Can they be used to count anything? What have they been used for? 

I would like to go deep, so any guidance you have would be most appreciated.  

Thanks.

I answered, starting with the history:

Hi, Michael.

This site, listed in our FAQ under Math History, should be your first source for questions on history:

   MacTutor Math History Archive
   http://www-history.mcs.st-and.ac.uk/ 

In particular, you will find some relevant material under the history of zero:

   http://www-history.mcs.st-and.ac.uk/HistTopics/Zero.html 

Check the link on Brahmagupta for some further details on the earliest use. The Chinese also used negative numbers very early, writing them in black and positive numbers in red. Negative numbers were not taken seriously, though, until the time of Cardan and Stifel, whom you can look up there; and it was not until some time later that negative numbers were given "equal rights" with positives, so that one did not need to know ahead of time whether a value was positive or negative.

We have some discussion of this topic here (check out the links):

   Negative Number History
   http://mathforum.org/library/drmath/view/52593.html

The “equal rights” idea means that until then, negative numbers were not considered valid answers, just a trick to use in the middle of a problem. We’ll be seeing that this idea continued long beyond Cardan (1500’s).

To answer your specific questions, I would say that negative numbers were invented not to count anything (unless you think of "counting" a debt, which is how Brahmagupta described the concept), but in order to make it much easier to work with equations. 

The best example I can think of, however, is beyond your students, unless you just show them the problems without going into the solutions. This is the solution of quadratic equations. Until the use of negative numbers, each kind of equation had to be treated separately: 

    x^2 + ax = b
    x^2 - ax = b

and so on. Once it was found that negative and positive numbers could be handled in the same way, the same methods could be used for all quadratic equations, since all could be expressed in the same general form by allowing variables to be have either sign:

    x^2 + ax + b = 0

(Note that if a and b are positive, this has no positive solutions, so they would not even have considered it.)

The Hindu mathematician Brahmagupta (600s) solved at least the first form; later authors such as Bhaskara (1100s) did allow negative coefficients and even (to some extent) negative solutions. Uniting all these forms into one meant there could be one method, and one quadratic formula.

In my mind the most significant use of negative numbers is in coordinate systems. We can locate points going both left and right, up and down from an origin, which would be impossible using only positive numbers. We would have to find an origin for which all points of interest were on the same side. So allowing negative numbers frees us up to describe things that happen anywhere in space, such as orbits of planets or graphs of equations. (Similarly, by allowing negative temperatures, we don't have to use a scale that starts at the lowest temperature we can observe; that's how the Fahrenheit scale originated, as a way to avoid negative numbers.) So really the number line is the central concept in working with negative numbers. Without them, we can't name all the points on the line, but only "half" of them.

Imagine having to fit everything you are working with into one quadrant of the coordinate plane!

But Fahrenheit’s scale, in which 0 was the lowest temperature they could achieve in the lab using salt and ice mixtures, was just as reasonable as the IRS decision to use only positive numbers.

Making things easier

Here’s one from 2004:

Why Do We Learn about Negative Numbers?

Why do we have to learn about negative numbers?  The only context where I can see it being useful is in determining temperature.

My child is just being introduced to negatives and both he and I are having difficulties with the subject.

Doctor Ian took this:

Hi John,

Strictly speaking, there's nothing we can do with negative numbers that we couldn't do without them. It's just that they make some things easier--in particular, they relieve us from having to worry about special cases when dealing with subtraction.

For example, suppose we're talking about longitudes.  We could always talk about "degrees east" or "degrees west".  But then we have to have a bunch of rules for subtracting longitudes, e.g., 

  a east - b east = (a - b) east if a > b

                  = (b - a) west if b > a

But if we just decide that east is positive and west is negative, then we can just subtract, 

  a - b = whatever

and let the sign keep track of the direction of the result, using a few simple rules.

This is very much like the IRS version, isn’t it? Signed numbers unify cases. We do often use directions in stating latitude and longitude, as in N38.889°, W77.035° or even N38°53′ 20″, W77°2’6″; but in calculations you would use (38.889, -77.035).

But the main reason for having to learn about them is that everyone _else_ is learning about them, and so if you don't learn about them, you won't be able to understand what other people are talking about in a wide variety of situations--which is kind of like moving to a foreign country and deciding that you don't really need to learn the language.  You can live that way, but you miss out on a lot. 

Does this make sense?

John replied,

Thank you very much for your prompt and very informative answer, this has clarified the situation for us.

A world of its own

Finally, a great question from 2008:

Negative Numbers in Real Life

I'm finding it very difficult to imagine negative numbers outside of math.  I've read some examples of their use here and elsewhere, but I'm still flabbergasted. 

I understand negative temperatures, because they're based on the temperature of water.  The temperature of frozen water is 0°C. Anything below is negative.  But measurements are a concept.  My trouble is with more concrete things. 

Mathematically, I can subtract 6 apples when I only have 5.  I can't do this in reality.  I can use negative numbers in math, but outside of measurements, I can't really grasp them in the real world.

For example, I can't have negative money.  After I'm bankrupt, I can't spend any more money (without going to a bank or getting a credit card).  But in the "world of math", I can take $600 from $500 and get -$100. 

I'm looking for an example where negative numbers work in the "real world" without measurements.  How can the math be accurate but impossible?

I answered this one:

Hi, Cody.

One thing that can help is to realize that mathematics is a world of its own that can be used to MODEL things in the real world, but, like any model, is not IDENTICAL to that real world.  Negative numbers are part of the "model world", not the real world.  So there are some situations where negative numbers make sense (and a negative answer to a problem is valid), and others where they do not (so that a negative answer just means there is no solution to the original problem).  In the case of temperatures, the 0 point (except in absolute temperature) is arbitrary, so that SOME negative values are possible, but others are not.

That is, when we apply math, we are “mapping” the problem into abstract models that match the way the real world works only up to a point. Then we “map” our answer back into a world where some answers just mean “can’t do it”.

In the case of money, a negative answer may or may not be valid.  If you are just spending money from a basic checking account, a negative balance means that you are overdrawn--but it DOES still have meaning, because you now owe that much money to the bank.  If you have an account with automatic overdraft protection, the negative balance means that you have borrowed that much and have to pay it back.  So how to interpret the negative result depends on the situation; often positive and negative are just two sides of the same coin, each with its own interpretation.

So sometimes positive and negative mean “gained” vs. “lost”, and other times negative money means you did something wrong.

The idea of negative numbers was often considered suspect even into the 1800's.  I've read a book by a mathematician of that time trying to present algebra in a way that didn't treat negative numbers as real; he called them fictitious, and presented them as just a shorthand for operations that should properly be done in reverse.  But he admitted that using negative numbers made the work easier, always gave the right answer (when interpreted correctly), and unified what would otherwise have required several cases (depending on which number is greater, for example).  That is, negative numbers serve as a good, though imperfect, MODEL--you don't have to recognize the existence of the negative numbers themselves as concrete entities in order to make good use of them.  (And, by the way, even counting numbers are really an abstract concept too--you never saw a "three" by itself, did you?  ALL numbers live in the math world, not the real one.)

This book was Augustus DeMorgan’s Elements of Algebra (1837), which you can read here:

After 20 pages of explaining how to “correct” “impossible” operations, he says,

We don’t follow his line of thinking today (if anyone else ever did); but he demonstrates that negative numbers work so well that even if you don’t consider them real, it makes sense to pretend they are! The idea of seeing signed numbers as an abstract concept independent of (though related to) the real world, has rescued us from this.

What we are doing when we use negative numbers is translating a real problem into a problem about, say, locations on a number line (which correspond to amounts of money you have or owe, say), solving that new problem, and then deciding how to translate the answer back into the real world problem.  The negative numbers live in this separate world of math, and may have various meanings or lack of meaning in the real world.

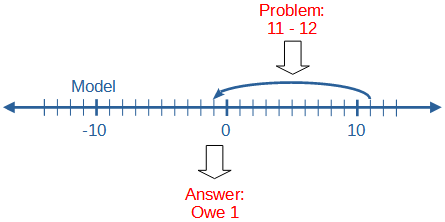
Cody wrote back:

Now THAT was a well put together answer.  It's more clear now, thanks.