Talking About Negative Numbers

Last week we looked at what negative numbers mean; here we’ll consider a number of questions we’ve been asked about the terminology of signed numbers: what “negative” means, and other words for negative numbers.

Up, down, and opposite

This question from 1998 asks about translating words to signed numbers:

Converting Words to Numbers

Can you solve this problem? 

Tell me an integer to describe each situation:

  1. 5 degrees below zero
  2. a loss of 7 pounds
  3. a gain of 10 yards
  4. positive twelve
  5. 3 feet below sea level
  6. 2 degrees above zero

Tell me the opposite of each integer:

  7.  -8
  8.   9
  9. -15

I answered:

Hi, Cambree, 

The first set of questions deals with what we call "conventions"; that is, people who use math have generally agreed that certain "directions" should be "conventionally" thought of as "positive." Anything that is "up" or "forward" or "increasing" or "more" is positive, and anything that is "down" or "backward" or "decreasing" or "less" is negative.

In general, “positive” is taken to mean “in the direction we expect” while “negative” means “the opposite of that”. So we need to know what is “expected” in a particular context, which is commonly implied by the words used.

For example, if I make a profit of 5 dollars in my business, I would call that +5, and if I lose 5 dollars, that would be -5. Why? Because then whichever happens, I can add that number to my bank account to find out how much I have now. 

Similarly, if a mountain's base is 2 miles below sea level and its peak is 3 miles above sea level, then the altitude of its base is -2 and the altitude of its peak is +3, so the total height is (+3) - (-2) = 5 miles.

“Positive” tends to correspond to adding, “negative” to subtracting.

On the other hand, as I said, these are just conventions, and they really depend on what you're measuring. If I were in a submarine measuring depth, I would say my depth is +2 miles, because when I think about "depth" I mean something that increases as I go deeper. So a depth of +2 means the same thing as an altitude of -2.

Therefore, the answer to these questions should include some sort of label. For instance, I would say "altitude = -3" for problem 5. You could also say "depth = +3" if you want to confuse your teacher, but then you'd have to bring me in to testify on your behalf, so maybe you'd better stick with -3.

I have too often seen textbook questions that are ambiguous because it isn’t clear which perspective to take.

You should be able to do the rest by looking for words like "below" or "loss" to indicate a negative number. Or look on your thermometer and see what they call a temperature below zero.

Let’s answer them all, since the problem was due long ago:

1. 5 degrees below zero = -5 degrees
2. a loss of 7 pounds = -7 pounds “gained”
3. a gain of 10 yards = +10 yards gained
4. positive twelve = +12
5. 3 feet below sea level = -3 feet in “altitude” [but +3 feet of depth!]
6. 2 degrees above zero = +2 degrees

I put the negative numbers’ units in “scare quotes” because you would not normally call, say, a loss of 7 pounds a gain; as I said above, this is contrary to expectations. The main use of such numbers is in formulas where a variable might be defined as a gain, and the negative value represents a loss. The fact is that, if we made a formula concerned with weight loss, we might actually expect a loss, and call a gain a negative loss. It all depends on what we call the quantity.

As for the last three questions, "opposite" just means to flip the number line around (stick a pin at the zero and give it a spin) and see where you land. The opposite of -3 is +3, and the opposite of +3 is -3:

   ------------------+----------+----------+------------------->
                    -3          0         +3

flips around to give:

   <-----------------+----------+----------+--------------------
                    +3          0         -3

so that -3 is where +3 belongs.

Just as in the words we use, “negative” means “opposite”. In fact, “opposite” is not used as a technical term with this meaning in math; many mathematicians would object to this very question. Instead, we say “the negative (or additive inverse) of -3 is +3”. But as we’ll see next, that can confuse students, so it is often avoided at first.

Answering the remaining questions,

7. opposite of -8 = +8

8. opposite of 9 = -9

9. opposite of -15 = 15

I hope this helps. Negative numbers aren't hard, but if you're confused, just remember that a few hundred years ago people thought mathematicians who talked about negative numbers were crazy. Let me know if you need more help.

We saw last week that even some mathematicians less than 200 years ago thought the idea was nonsense!

Negative vs negative of

This is from later in 1998:

Solving -x = 3

Please tell me how to get the answer to -x = 3. I have no idea how a negative can equal a positive.

We use “negative” in two different ways: a negative number is one that is less than zero; the negative of a number is the opposite of that number (which may be positive or negative, depending on the starting number).

Doctor Roya answered, avoiding this confusion by sneaking in the back door:

Dear Tyler,

Thank you for writing to Dr. Math.

We are going to try to solve this problem backwards. By that I mean, we are going to look at the answer first and work our way back to the original problem.

Let's look at the following example: 3 is a positive number. If we multiply 3 by -1, we get -3, which is a negative number. We say that -3 is the opposite of 3.

In fact, the symbol “\(-3\)” means “the negative of 3″, which is the same idea as “opposite”. The negative of a positive number is a negative number.

In the same way, 3 is the opposite of -3. How, you may ask? Well, just do the same thing. Multiply -3 by -1. We get (-1)(-3) = 3. 

If we drop the 1 in this new equation (we are allowed to drop the 1, since 1 times any number is that same number), we end up with:
   
   - -3 = 3
 
This is becoming more familiar, isn't it?  

Now, if we replace -3 with a variable (unknown) x, we end up with:

   - x = 3 

which looks just like your problem.

Again, the negative of a negative number is positive.

So this just happens to be the solution: If \(x=-3\), then \(-x = 3\).

Going back to your question:

If we read the equation (-x = 3), it says: We have a number x, that when we multiply by -1 the result is number 3. What number does x represent? 

Remember that (-1)(x) = 3 is really the longer way of writing the same equation. I hope that you now see how x must be a negative number. In fact x is equal to -3. 
 
Please keep in mind that x stands for a number. That number could be a positive number or a negative number. x is just a place holder. Please write back if you still have questions.

In solving this equation, we can just divide both sides by \(-1\), the coefficient of x. Or we can just say we are taking the negative (opposite) of each side: $$-x=3\\ -(-x)=-(3)\\ x=-3$$

Is zero a negative number?

Here’s a question from 2001 clarifying the definition of “negative”:

Is Zero Positive or Negative?

Is zero a positive or a negative number? People consider it neither. I don't get it.

Two of us answered; first, Doctor Jaffee:

Hi Beth,

In order for a number to be positive, it has to be larger than 0.   
So, 0 is not positive.

In order for a number to be negative, it has to be smaller than 0.   
So, 0 is not negative.

Therefore, 0 is neither negative nor positive.

Doctor Roy got his answer in less than two minutes later:

Let's reconsider what it means to be positive or negative. To be positive, a number must be greater than zero. To be negative, a number must be less than zero. If you read these two definitions carefully, you notice that the number zero is not covered by either case. So, the concept of positive and negative includes almost all the numbers, but it does not consider zero. Zero is considered special. By definition, it is neither positive or negative. 

Think of the number line as split into three parts: negative, 0, and positive, as follows:

      -5   -4   -3   -2   -1    0    1    2    3    4    5
   <---|----|----|----|----|----|----|----|----|----|----|--->

   <------ negative------------>0<-------------positive------>

I hope this helps, and please feel free to write back.

Zero is the border between positive and negative. A number that is “non-negative” can be either positive or zero.

Is zero a signed (or directed) number?

This question, from 2002, raises one more important distinction:

Is Zero a Signed Number?

Please tell me, Dr. Math,

Is zero a directed number? What is the direction of zero? If zero is not a directed number, why do we use it in the set of directed numbers?

Example: When we place directed numbers in line:

   -4, -3, -2, -1, 0, +1, +2, +3, +4

I answered after checking this relatively unfamiliar term:

Hi, Intisar.

Probably you are using "directed numbers" to mean something like "signed numbers"; it appears that this is a British school term for what we would properly call "integers" or "real numbers," with the emphasis on the presence of a sign. It is meant to be descriptive, not a precise definition, and I think you may be taking the term too seriously.

I would say that "the set of directed numbers" refers to numbers in which we are allowing both a length and a direction (sign). In the case of zero, the direction is meaningless, since +0 and -0 are the same; but that does not mean that it has no sign, only that the sign makes no difference.

As I mentioned last week, “integers” doesn’t just mean “signed” but also “whole”; mathematicians don’t commonly need the terms “signed” or “directed”, but they are useful when you first encounter the concept of sign.

When we write “-0” or “+0”, we are writing a sign, which would not be allowed if we were treating it as unsigned. We are not saying that 0 in itself has a sign (that is, is either negative or positive), as we just saw.

The important point about the set is not that each member of the set _must_ have a significant "direction," but that directions are _allowed_, so that the set does not consist only of positive numbers. That is, no claim is made that you can separate out the size and direction for every such number, so that each number (including zero) should have a specific direction; rather, numbers in the set are built by combining a "size" and a "direction" (sign), and there is nothing wrong with both +0 and -0 turning out to be the same number.

A similar issue arises with vectors, which are described as having both length and direction; there, too, the zero vector doesn’t actually have a direction.

Moreover, I would not even say that any particular number is "a directed number"; rather, a number like 1 (or 0) may be treated either as a mere number (by children who have not yet learned about negative numbers, or when only positive numbers make sense), or as a "directed number" in contexts where signs are meaningful. It is really only "the set of directed numbers," or "operations on directed numbers," that are significant, not the individual numbers.

In computer programming, a variable can be specified either as a signed or an unsigned number; this affects how it is stored (in effect, whether there is room for a sign), and what can be done to it.

If we tried to formally define the "integers" (directed whole numbers) or the "real numbers" as numbers that combine size and direction, we would have difficulty in stating clearly what we mean. But if you are using "directed numbers" just to indicate that you are working with numbers with (optional) signs, and not as a formal definition of a set, then there should be nothing wrong with accepting that zero belongs in this set.

Teaching negative numbers

I’ll close with a question from a teacher in 2003 that touches on several of the topics we’ve seen both here and last week:

Talking About Zero, Absolute Zero and Negative Numbers

Zero is a tricky number to explain, especially when children are interested in why we have negative numbers.  It is difficult to conceptualize taking something away from nothing.  It becomes even trickier when thinking about absolute zero.  Are there any useful strategies other than temperature to introduce negative numbers, and also to teach about zero, its properties, and how they differ from absolute zero?

I answered, starting with “absolute zero” and temperature:

I'm not sure what you are asking about absolute zero; I'm only familiar with that term as a temperature, and as far as numbers themselves are concerned, absolute zero is just zero.  The only special thing I see about it is how it fits into the scale: in the case of Kelvin temperature, we have a scale with a definite starting point, and negative temperatures do not exist (though I understand that this is not really quite true if you dig deep enough into the physics of temperature!).  On the other hand, in scales where no (known) lowest value exists, negative numbers have to be allowed, and zero becomes not an absolute end point, but a mere reference point along the scale from which quantities are measured in both directions.  If the concept of absolute zero temperature had not been discovered, then we could not have a Kelvin scale, and all temperature scales would have to, at least theoretically, allow for negative temperatures.

Temperature is not only a good place to see negative numbers, but also a model of the difference between applications that allow them, and those that do not. Here are the Kelvin, Celsius, and Fahrenheit scales for comparison:

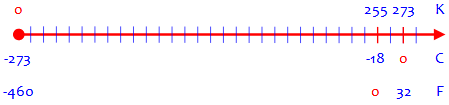
Kelvin starts with zero as the lowest possible temperature, so in principle it is a set of unsigned numbers. But Celsius puts zero at the freezing point of water, and Fahrenheit at the lowest temperature obtainable in the lab at the time, making them sets of signed numbers. The latter both allow negatives, though not all negatives are possible.

There are some situations where only positive numbers make sense, and in those cases we have the equivalent of a Kelvin scale, with an absolute zero.  For example, a person's height can't be negative; no one can be less than zero meters tall!  But altitude, which on the surface sounds the same, does allow negatives; I can be 100 meters above sea level, or 100 meters below sea level (a negative number).

Again, we can find an alternative scale for altitude that has an "absolute zero", namely the distance from the center of the earth; so altitude referenced to sea level is just a convenience for people who live near sea level (as Celsius is convenient for people who "live" in the zone where water is liquid).  But not all scales can be made absolute; coordinate systems for space offer no (known) "farthest left" location, so negative numbers are required no matter what you do.  Which leads into my next comment ...

Here are the two altitude scales (using miles, rounded), with zero at the center of the earth and at sea level, respectively:

The International Space Station is at 4250 miles from the center, but 250 miles above sea level.

Apart from temperature, I think the only good way to introduce negative numbers is with a number line (of which temperature is just a familiar example we can point to in a child's environment, especially when they live in a cold climate).  If you look at what we say about negative numbers, such as

  Positive and Negative Integer Rules
  http://mathforum.org/library/drmath/sets/select/dm_pos_neg.html 

you will find a lot of references to the number line.  The basic idea is that, if we want to locate every point on a line by associating it with a number, positive numbers just aren't enough!  In order to put any numbers on the line in numerical order we have to have a zero point from which we start counting; and in order to label points in both directions, we need negative numbers.  Once you have that idea of negative numbers as labels for points to the left of zero on a number line, everything else falls into place.

Positive numbers (actually, non-negative numbers!) are appropriate for measuring on a ray, which goes in only one direction; for a line, or anything else that can extend without bounds in either direction, we need negative numbers to be available.

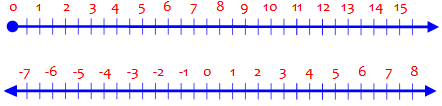
After building that view of negative numbers, you can return to counting situations and ask whether negative numbers ever make sense there.  That's when ideas of "owing" or "debt" arise as uses for negative numbers.  But probably those ideas won't be clear without the number line model to make the concept concrete.  In a sense, we are then modeling counting in terms of the number line, extending the idea of number to allow for negatives that result from subtracting more than you have.  Such modeling is really the essence of mathematics.

This is the idea we closed with last week.

Next time, I’ll look at two more questions that would have made this post too long; they are about the difference between “negative” and “minus”. How are negative numbers and subtraction related, and how are they different?