Last time we looked into terminology related to negative numbers; one subtopic was too big to fit, so I’ve broken it out into a separate post. How are the concepts of “negative” and “minus” (subtraction) related? How much do we need to distinguish them? We’ll look at two questions, the first from a child focused on the words, which are often confused, and another from an adult wanting to untangle the symbols, which are normally identical though they have different meanings.
Two different things
First, from an anonymous student in 2002:
Negative 5 and Minus 5 Can you tell me the difference between negative five and minus five? When should I use negative? When should I use minus? If I have a lot of numbers, e.g. +3 ,-7, -3/4, -5.4, 1/4....... How to read them? Thank you!
[Note: If this sounds totally foreign to you, you should read the discussion in the comments below, which points out that this appears to be a largely American usage; this question and answer assume that context.]
Rather than give a routine answer, Doctor Achilles started with a bit of history:
Thanks for writing to Dr. Math. That's a very good question. It's very easy to get negative 5 and minus 5 confused because people often say "minus 5" when they should actually say "negative 5." I'm going to answer this in a sort of roundabout way that I hope will help get the point across. A long, long time ago, people thought only in terms of the natural numbers: 1, 2, 3, 4, 5, ... You can do a lot with the natural numbers. You can count how many sheep, dollars, children, and friends you have. You can count how many apples you have. You can even do simple arithmetic: if you have 6 apples and you lose half (divided by 2), you end up with 3 apples; if you have 6 apples and you double the number (times 2), you end up with 12 apples; if you have 6 apples and you get two more (plus 2), you have 8; if you have 6 apples and you lose two (minus 2), you have 4. The idea of subtraction (or minus) has been around since the days before fractions and integers, when people only thought in natural numbers.
Before there were negative numbers, there were operations. Subtraction was read as “minus”, which is Latin for “less”, another term that is sometimes used: “nine minus five” or “nine less five”. (Adults don’t say “nine take-away five”.)
If I say "nine, five" to you, all I have done is list two numbers: 9, 5 I haven't told you anything about what to do with those numbers. The most you can do is just remember them. You don't know whether I want you to multiply them, divide them, add them, or just remember both of them (one could be the number of oranges I have and the other the number of cousins I have). If I say "nine plus five" to you, then I have told you to add two numbers. You don't have to remember 9 and 5, you just have to know that the answer is 14.
The point is that the words “plus” and “minus” represent operations.
Somewhere along the line, some people came up with zero (and that was a big deal) and some other people came up with fractions (and that was a big deal). Then some other people came up with integers. Integers are all the positive (natural) numbers, and zero, and the negative numbers: ..., -3, -2, -1, 0, 1, 2, 3, ... It's hard to think of apples and sheep in terms of negative numbers, but they are useful in thinking about money and other things. For example, right now, my bank account has a negative amount of money in it. Negative numbers are just a kind of number, not really any different from positive numbers.
The word “negative” describes a number.
If I say "nine negative five" to you, all I have done is list two numbers: 9, -5 I haven't told you anything about what to do with those numbers. The most you can do is just remember them. You don't know whether I want you to multiply them, divide them, add them, or just remember both of them (one could be the balance in my friend's bank account and the other the balance in my bank account). If I say "nine minus five" to you, then I have told you to subtract 5 from 9. You don't have to remember 9 and 5, you just have to know that the answer is 4. So "negative 5" is a number and "minus 5" is a mathematical operation you can do to another number. If it helps, you can think of "negative 5" as a noun, as in the sentence "negative 5 is my least favorite number"; and you can think of "minus 5" as a verb as in the (ungrammatical) sentence "I want you to take 9 and minus 5 it."
Unfortunately, people do often use “minus” in place of “negative”; my dictionary even gives the example “minus ten degrees”. It can be hard to keep straight!
One other thing. This tends to get complicated when you start doing crazy things like: "negative 5 plus 6" or "8 minus negative 5" If you want, you can check out this page for my suggestions of how to deal with this: Tips for Negative and Positive Numbers http://mathforum.org/library/drmath/view/57873.html I should note that I'm a bit sloppy with the distinction between "minus" and "negative" on that page.
He isn’t very sloppy; he just uses “minus” to refer to the symbol, however it is being used.
He closed by giving the words for +3 ,-7, -3/4, -5.4, 1/4 in the question:
For the last part of your question, the list you gave reads: "positive three" OR "three" "negative seven" "negative three-fourths" "negative five point four" "one fourth" OR "one quarter" Hope this helps. If you have other questions about this or anything else, please write back.
The student did write back:
Dear Dr. Math, I think your answers are great help to me. Thanks again. Can you answer another question? I'm reading a book called _Exploring Mathematics_. It says "Weather-forecaster: The temperature fell to 'minus five degrees'." Is it right? Thank you. Best regards!
Doctor Achilles replied,
In English it is not uncommon to hear "negative 5" called "minus 5." This is technically incorrect, but if you're not speaking with mathematicians, then it's acceptable to just use "minus 5."
Everyday language is not precise.
One symbol, two meanings
Our second question, from Chris in 2005, is about the symbol:
"Subtraction" and "Negative"--Same Sign, Different Concepts? Is there a difference between the operation "-" when used in the expression "y = a - b" as compared with its meaning in the expression y = -b? I don't doubt the truth of the statement 0 = -1 - (-1) but the reasoning I have seen has never quite convinced me, because it seems that the - sign is being used to mean two different things. On a number line these two things are something like 1) -b => Rotate the following number by 180 degrees. 2) a - b => Continue (or count) in the direction of the following number, rotated by 180 degrees. Now while these are fairly similar they are not the same thing. Taking another approach, we are allowed say "y = a × b" but we are not allowed to say "y = × b". So "-" is being used in a "syntactically" different way to "×". This indicates to me that we are allowing "-" to be used to mean two different things. I think that, as it happens, the rules for combining the two different meanings of the sign allow us to get away with saying "-(-) = +" without distinguishing between the two, because it just happens to work out like that. The reason I'm so hung up on this is that I think if we temporarily used new signs - say, p and n, for positive (no rotation) and negative (180 degree rotation)--and continued to use + and - for the operations of counting on or counting with rotation, it all becomes a lot easier to explain what is actually happening. That is, "pa - pb" can be shown to be the same as "pa + nb" and also it is much easier to grasp that "pa - (nb) = pa + pb". Is there anything to all this?
We often think of the negative sign just as part of the name of a number (which is how Doctor Achilles used it in his answer above); Chris rightly sees it as an operation (the “negative of” that we talked about last time). But that means we are using one symbol to represent two different operations. Would it be helpful to use two different symbols?
I answered:
Hi, Chris. You're exactly right that "minus" and "negative" are two different operations; that's why they have different names (and we _try_ to get kids to use the right names ;-). "Minus" is a binary operation (performed on two numbers), while "negative" is a unary operation (performed on a single number). They have the same symbol because they are _very_ closely related, and it doesn't cause any trouble to use the same symbol.
This is, ultimately, the same idea Doctor Achilles was emphasizing: Minus and negative are different things. But now we need to explore how they turn out to be related so closely that, even though we use two different words, we can use the same symbol. And distinguishing them will help us to see this!
Alternative symbols
However, some texts have done just what you suggest, and used different symbols for them; one common choice is a raised "-" to mean negative, so an equation might look like
_
a - b = a + b
This does help some students to get a better sense of the distinction before they move on to the normal notation.
This notation looks like “\(a-b=^-\!b\)” or “2 + ⁻3 = ⁻1”. It isn’t the only notation that’s been used.
You may recall that two weeks ago we saw that DeMorgan represented negative numbers by a bar over the number, as seen here (p. 46):

His \(\overline{4}\) wouldn’t work so well as an operation, but was a reasonable attempt to distinguish negation from subtraction. The same idea has been used in balanced ternary notation, e.g. \(10\overline{1}_{bal3}=1\cdot 3^2+0\cdot 3^1+(-1)\cdot 3^0=8\).
Cajori mentions several mathematicians who used each of these notations:
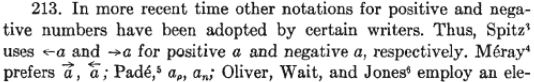

I might also add that scientific calculators have separate keys for the two operations; on those that most closely mimic written math notation, the "negative" key is commonly labeled "(-)" to distinguish it from the "minus" key, "-".
Here are two such calculators, with green “minus” and yellow “negative”:

Other calculators, in which operations apply to the number in the display rather than being entered as they would be written, use a “change sign” button instead (red here):

Computer programming languages don't need to make that distinction, since they can determine the meaning from context; I'm not sure why calculators don't do the same, but it's probably due to little differences in the way users think of keys on a calculator vs. characters on a page.
Here’s one difference between calculators and programming, that explains the need for the separate button: In a program, each statement has a definite start, so if you type, say “– 2 – 3”, it is clear that the initial “–” is a negative sign, because there is nothing before it. But in many calculators, if you enter “– 2 – 3”, it will assume you are continuing a calculation using whatever was previously calculated, so that there is in fact something before the sign; some, for example, will display “(ans) – 2 – 3”. If the display previously showed 0, the result will be what you expected, but otherwise you will be subtracting 5 from the previous result. The separate (–) button prevents this from happening.
Aside: A similar issue arises with students, who may confuse \(a-b\) with \(a(-b)\), especially in larger expressions. How can you tell whether “–” is a subtraction, or multiplication by a negative? This was discussed near the end of Order of Operations: Subtle Distinctions; the answer, as I just explained for computers, is this:
If an expression can be interpreted as a subtraction, it is a subtraction. For example, \(2-3\) is a subtraction because the “–” is between two numbers; but \(2(-3)\) can only be a multiplication, because there is no number on the left of the “–”. To show multiplication by a negative number on the right, the parentheses are required.
On the other hand, there are some programming languages with very different syntax, in which the distinction is needed. I vaguely recall the “high minus” symbol (raised negative) from my long-forgotten introduction to APL (one of the first languages I learned, in the 60’s); it is used like DeMorgan’s bar, not as an operation, but as an integral part of the numeric “literal”.
Subtraction as adding the negative
Regardless of whether we use distinct notations for the two operations, it is important to distinguish the operations themselves. The negative is called the "additive inverse", and is defined by a + -a = 0 That is, the additive inverse of a is the number you can add to a to get 0. Having defined that, we actually _define_ subtraction in terms of this: a - b = a + -b That is, we define subtraction as _meaning_ addition of the additive inverse; so, as you said, subtraction means "turn around on the number line and walk the given distance in the opposite direction". This is the connection between the two operations, and the reason it is helpful to use the same symbol. When I read "a - b", I see it as "a + -b", because addition has important properties, such as commutativity, that subtraction lacks, making it very useful to forget about subtraction and use only addition.
This definition of subtraction as “adding the opposite” can’t be used before students have learned about negatives, or in contexts dealing only with natural numbers. There, we define subtraction as the inverse operation of addition. That is, the difference \(a-b=c\) is the (unique) number \(c\) such that \(a=b+c\). Subtraction “finds the missing addend”. This produces the same result as adding the negative because, using the definition I gave above, we can see (1) that \(c=a+-b\) satisfies the definition: $$b+c=b+(a+-b)=b+(-b+a)=(b+-b)+a=0+a=a$$ and (2) that if \(a=b+c\), then, adding \(-b\) to both sides, $$a+(-b)=(b+c)+(-b)=(c+b)+(-b)=c+(b+-b)=c+0=c$$ so that \(c\) is unique.
Once we have the concept of additive inverses (which necessitates knowing about negative numbers), algebra becomes far easier. Think about the fact that algebra existed before negative numbers were accepted, so that (as we saw two weeks ago) we needed separate cases for everything!
(Note that if we used a very different symbol, like your "n", it would be harder to see the connection and to learn to see it this way: it is not obvious that a - b = a + nb.)
This is the benefit of “raised minus” notation: It’s enough like regular minus to see the connection, yet distinct enough to help students.
There is a similar issue with regard to multiplication and division. If we wanted, we could use the division symbol "/" to indicate the multiplicative inverse (also called the reciprocal): a * /a = 1 We define division as multiplication by this inverse: a / b = a * /b in much the same way as for subtraction. For some reason this has never caught on, as far as symbols are concerned. Similarly, although we can use "+" as a unary operator (which has no effect on a number, as +a = a, meaning 0+a), we don't happen to use multiplication, "*", in the same way, so that *a = a, meaning 1*a. It wouldn't hurt to do so, but has not been found useful!
In reality, rather than this “raised division”, \(a\div b = a\times ^\div\!b\), we use a negative exponent to indicate a reciprocal: \(a\div b = a\times b^{-1}\). This could be used, for example, in Order of Operations: Common Misunderstandings.
Getting back to negatives, the fact that -(-a) = a (effectively, turning around twice and ending up in the same direction) allows us to easily rewrite -1 - (-1) as -1 + -(-1) = -1 + 1 = 0 This is much harder to explain in terms of subtraction only; by seeing subtraction as adding the negative, it becomes relatively simple. In summary, your thoughts are valid, and not really new; seeing things this way is actually essential to learning algebra well. So you're in good company!
Chris responded:
Fantastic! To some small degree I have been hung up on this for years and despite moderate searching I have never come across any of these texts, so it is quite a relief for me to find that it is a valid way of thinking. Thanks again for your time.
More on the raised minus
I did some searching of my own, hoping to find examples of the raised negative in modern materials; but at the time that was hard to find; the only source I found no longer exists. It is easier to find references to it today; one reference I find to it, here, says
A simple and useful example is the use of two different “minus” signs in school (at least in the USA), the normal “-” sign for subtraction, and the raised minus sign for indicating a negative number, ⁻7 for negative seven. This notation, typically in use up to 8th grade, allows the text books to write 8 – ⁻7 rather than having to write 8 – (-7), for instance. Teachers typically think of this negative number notation as a kind of training wheels.
Wikipedia mentions it (here) without citation. American teaching standards don’t mention it. But I find examples of teaching materials using it from the U.S. (1972), the U.K. (expand Use negative numbers in context), Australia (e.g. pp. 14-18), New Zealand, and even the Philippines. (If you find better examples, let me know.)
Chris responded to what I showed him:
Thanks for this. Visually, the look of the expressions which mix the raised "-" and normal "-" are exactly right for me and express the meanings quite intuitively. The distinction between 5 - 6 and 5 + ^-6 is clear, as is the fact that they give the same result. Regards, Chris.

I have been a University scientist, in UK and Europe, for 50+ years and had never heard “negative 3” used in this way until I came across it on YouTube videos, where American presenters often use this new and strange terminology.
It is wrong, bizarre, and confusing to read “−3” as “negative 3”.
The unary operator is just that: an operator, with the name “minus”. In “−3” the “−” is NOT a property of the number, it is a function mapping one number to another.
“negative” refers to the property of a number, as does “odd”. I have never heard anybody read “−3” as “negative odd three”, which highlights the bizarreness of “negative three”.
When we use variables it becomes even more confusing. How would people speak the following:
x = −3
x = −y ?
y may or may not be negative (or odd for that matter) so it would be highly inappropriate to say “negative y” for “−y”, so “minus y” is the correct way of saying it. But the “−” serves the exact same purpose in each equation, so it would be confusing to say the equations differently.
Hi, Tony.
You raise two main points, both of which I find interesting: (a) that you had never heard “negative three”, and (b) that it is “bizarre”. I’ve taken the time to look into both (and found people arguing over this usage far more than it deserves).
First, I discovered that this terminology seems to be largely American. Some people (e.g. Wikipedia and Schwartzman) suggest that it was introduced as part of American “New Math” in the 1960s (which, if true, would work against your other claim, since that movement was led by actual mathematicians trying to correct poor ideas found in traditional textbooks, not ignorant non-mathematicians).
But in fact I’ve found both “minus 3” and “negative 3” used in an American textbook from 1905 and others like it; and I’ve found both forms at least mentioned in some British textbooks like this. (It’s hard to find explicit evidence of what mathematicians actually say when they read “-3”; textbooks at any level may not be representative of such actual usage.) So it isn’t really so new, or entirely American.
The Math Doctors are largely American, so we tend to teach what is taught here; but a good number of us have been elsewhere in the world, and I don’t recall any dissenting voices on this point. I can easily believe, though, that this usage is most common in America. And here, though we are typically taught to say “negative 3”, we do often switch to “minus 3”, and don’t make a big issue of it.
The more important issue is your claim that “negative 3” is “wrong, bizarre, and confusing”. It’s not uncommon for Americans to think British usages are bizarre, and vice versa. Having seen lots of variation in usage around the world, I try to avoid such critical judgments; I have no intention of convincing you to change to “negative 3”.
But is “minus three” inherently more rational than “negative three”? Is the latter objectively wrong? That’s worth thinking seriously about.
You say that “-” in “-3” is a unary operator, not a property of the number. I fully agree! That’s one of the points we make. The issue in question is whether it must be read as “minus” rather than “negative”. You assert the former, presumably assuming that we need separate words for operators and properties. Note that although the symbols for the binary subtraction and unary negation operators are the same, the operators themselves are distinct, and need not have the same name — in fact, it’s confusing if they do. The American preference (if that is what it is) is to help students see that distinction. That makes sense to me.
You say that “negative” is a property of a number. So it is; but it is also an operation (negation) that you can perform on a number: the negative (additive inverse) of a positive number is negative, while the negative of a negative number is positive. I agree that that can be confusing; for that reason many textbooks initially call it, say, “the opposite of x”, but my impression is that such terminology is considered informal. Your solution to that confusion is to call it “minus x”, but that can cause a different confusion, namely with subtraction.
(Your comment about “odd” is rather silly; there is no operator to change the parity of a number, as there is to change the sign, so there is no parallel. We don’t write “-” before a number to declare a property, but to modify the number.)
We do in fact read “-y” as “negative y”, meaning “the negative/opposite of y”; this does not mean that the result is a negative number. One has to realize that the adjective here does not mean that the number itself is a negative number, but that something has been done to the number to change its sign: “negative” has two different meanings (like many words in English). Yes, this is tricky. But, then, as you read it, “minus” has two different meanings!
My sense is that you find “minus” preferable primarily because you just think of it as a name for a symbol, and read the symbols rather than their meanings. That is a valid style, but just as arbitrary as other ways in which British and American English differ.
Ultimately, I think we have to recognize pros and cons on both sides. You prefer to use one name for the symbol, however it is used, and that makes sense. American teachers prefer to emphasize the meaning behind the symbol, and that makes sense too. Each style can lead to confusion; neither ought to be denigrated as if language could ever be “right” or “wrong”.
I would probably soften the statements that “minus” is wrong, and just say that it is useful to say “negative”; I suggest that you stop calling “negative” bizarre, and recognize that styles differ.
> You raise two main points, both of which I find interesting:
> (a) that you had never heard “negative three”, and
> (b) that it is “bizarre”. I’ve taken the time to look into both
> (and found people arguing over this usage far more than it deserves).
(a) I have attended conferences, and presented papers, around the world, including Maths conferences, and have never heard “negative 3” being spoken for “-3”, or similar. It has always been “minus three . . .”. This is a simple statement of fact.
(b) Bizarre: very strange or unusual. You confirm this by finding only American references that use this terminology. As USA is a minority of the English speaking world I stand by that claim – the usage is very unusual (i.e. bizarre). I have just attended a dinner with scientist and maths friends from China, Malaysia, Brazil, Australia, Scotland and Netherlands, and they too consider the usage strange and bizarre.
I note from Vector and Tensor Analysis, Borisenko & Tarapov (trans Richard A Silverman), Dover 1979:
“By the vector ─A (‘minus A’) […]”
so a published American Mathematician in the day considered unary “─” should conventionally be spoken “minus”.
I also note from your citation of the UK Instant Maths Ideas for KS3 Teachers: Number and Algebra, Colin Foster, Nelson Thornes, 2003:
Some people prefer to say “negative 3” rather than “minus 3”, saving “minus”
for operations (“negative” is an adjective; “minus” is a verb), although no-one does this with
temperature.
> You say that “negative” is a property of a number. So it is; but it is also an operation
> (negation) that you can perform on a number: the negative (additive inverse) of a
> positive number is negative, while the negative of a negative number is positive.
> I agree that that can be confusing
You agree that ─ as in ─3 is a unary operator. Negative is not an operation. Negate is, and had “Negate 3” been used I would have much less of an issue with that usage as, although unnecessary, it is less confusing. The Foster quotation identifies the problem: adjectives are properties, operators are verbs.
As negative is a property and and adjective I re-assert that the use of ‘negative’ as an operator is wrong. [Note: as wrongness is not an absolute property I mean that which is contrary to established (international) convention.]
You seem to argue that any confusion in the overloading of “negative” overcomes the confusion of overloading “minus”. Am I correct in that interpretation?
“minus 3” has been the conventional usage throughout by schooling, university education, and academic life, and I have never encountered any confusion with the terminology. What is the evidence that any confusion existed?
I’d like to see some academic citations to any research.
As a scientist I delight in being proven wrong.
It appears that I need to clarify a couple points in my response to you. (Why are you replying over a year later? It seems to me that you are “arguing over this usage far more than it deserves”.)
First, there is no need to prove that the usage “negative three” is not universally accepted; I have acknowledged that, and pointed out that our explanation of it was given in the context of American schools, where this is taught, and is not a claim that this is standard even in actual American usage. I said I found it “interesting” that you had never heard this usage, because I was not aware how closely it is associated with American teaching, and I was interested to learn that. I don’t deny your experience. You don’t need to convince me; I don’t need to prove you wrong.
On the other hand, I consider it offensive to use the word “bizarre”, which amounts to saying that American teachers are irrational. (Perhaps the word has a more moderate connotation in your dialect than in mine?) In my years of answering questions from around the world, I have run across many usages (in English vocabulary, and in notation), that surprised me, some of which I have found helpful, and others not so. I have tried, as I said, “to avoid critical judgments”, and to work within what a student is being taught, as much as possible. So if “negative three” had been some foreign usage unfamiliar to me, I would probably still try to explain why it is not irrational, rather than tear down that foreign educational system and promote disrespect for their teachers. Simple respect for other cultures is appropriate, and I do not put up with disrespect in comments on this site.
The main point of this post is not to recommend this terminology, but to point out the importance of recognizing the distinction between subtraction and negation, as well as the difference between “a negative number” and “the opposite of a given number”. I would not be surprised if “negative three” was introduced in much the same way as the “raised minus”, as a temporary terminology to help in talking about these differences, without being intended as something everyone should always use everywhere. (But the nature of the education system seems to be that simple rules intended for pedagogical purposes are transmuted into absolutes by people, teachers or students, who don’t know better. PEMDAS has had a similar history.)
Additional data would be interesting, to see when and where this usage actually originated, and what arguments were made for that introduction. I have not yet done enough research on that.
Pingback: Making Sense of Imaginary Numbers – The Math Doctors
Hello Dave
I was interested in the three meanings of a negative sign for my dissertation topic. Your web article gave me a lot of ideas and inspiration.
I have one question for you. Even though children fully understand what the three meanings of a negative sign are, why do they have so many errors in the Algebra problem including negative numbers? Is it just a matter of working memory?
Hi, Sen.
Your question brings to mind one mature adult student I spent time with this semester in my community college tutoring, who constantly dropped negative signs (eventually laughing at it as a running joke); it may well be a matter of working memory in her case.
But more generally, when I think about where I see sign issues in my work with students, there are two that stand out: subtracting negative numbers, as in x^5/x^-3, where they often just write x^2, thinking 5-3; and factoring with a negative, as in 3x^2+6x-2x-4, where they often write 3x(x+2)-2(x-4), getting the wrong sign for the last term. In the first case, the problem is that they are doing too much in their head, thinking “5 minusminus 3” which merges into “5 minus 3”; if they write out 5-(-3) they generally see it. You might consider this an example of a working memory issue; it’s just too hard to keep all that in your mind at once. The other case is mostly a matter of not thinking carefully enough, rushing through the end.
My recommendation for students in both cases is to slow down when they see a negative, and even more so when there are more than one in a problem. Slowing down can include writing more steps than they think they need, as in the first example, and thinking separately about each thing they do (“-2 times what is -4?”) in the second. Perhaps that, too, clears working memory to make more room.
So I like your idea!
I think (and treat them ) that plus and positive are the same, as are minus and negative. And they are not really operations.
4 + 3 is just simplifying 2 positive integers: 7
If you have $4 and your friend has $3 and you put them together, you get $7
When we put -3 together with positive 4, we just simplify them to 1
If you’re $3 in debt, but you have $4 in your pocket, you put them together to get $1
I don’t think it’s helpful to say addition is not an operation; your phrase “put together” is essentially what addition means, and you are definitely doing something to a pair of numbers, which is what an operation is. And you can’t say you are merely simplifying the two numbers; you are adding, which makes a new number.
And as I’ve said, although in the context of mere arithmetic it is natural not to think of negation as an operation, it is necessary to do so in algebra.
As a way of thinking about addition and subtraction, of course, what you say agrees with what we teach.