A question just after we recently discussed quartic equations, has special features that lead to a unique solution method. We’ll be showing how to use synthetic division, and seeing some interesting graphs.
Circular thinking?
Here is the question, from Jitender:
This problem is taken from the book: Problem solving strategies, by Arthur Engel, in Chap. 1 (“The Invariance Principle”) exercise #30.
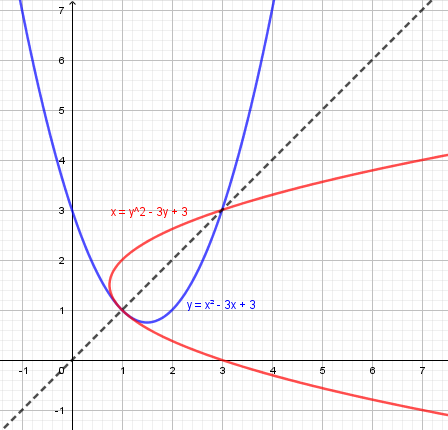
Solve the equation \((x^2-3x+3)^2 -3(x^2-3x+3) +3= x\).
I did this:
Let \(x^2-3x+3=y\),
\(y^2-3y+3=x\)
The roots of \(x^2-3x+3=y\) are: \(x=\frac{3\pm\sqrt{-3}}2\).
Now what to do further, seems a circular problem.
Half an hour later, he added more:
Sorry, didn’t know that book provides solution:
I answered first, not quite seeing what he was doing:
Hi, Jitender.
It’s a nice problem, and a well-explained solution using a trick I might not have thought of (though the chapter title might have suggested it). I presume reading that chapter would also be useful!
One comment I can make is about your work here:
Let \(x^2-3x+3=y\),
\(y^2-3y+3=x\)
The roots of \(x^2-3x+3={\color{Red}y}\) are: \(x=\frac{3\pm\sqrt{-3}}2\).
You solved x2 – 3x + 3 = 0, not x2 – 3x + 3 = y.
Do you fully understand the solution?
Since I’ve just written a couple posts on solving quartic equations, which is what this problem is, I have to also point out that if you expand the original equation, you will find that the leading and trailing terms are 1 and 3, so that the rational root theorem tells us to that the only possible rational solutions are ±1 and ±3, so we would quickly find the solutions without the tricky method the author used. But his solution is far more interesting, and would apply to harder problems (as long as they are carefully designed to yield to this approach)!
Sometimes all you can do is to expand an equation and use standard methods; but when it is presented in an interestingly arranged form, it’s a good idea to try to use what you’re given!
Composition of a function with itself
Doctor Rick saw more than I had seen:
Hi, Jitender, I would like to add some comments from another perspective.
Second, my first thoughts when I read the problem were a little different. When you wrote,
Let x2 – 3x + 3 = y,
y2 – 3y + 3 = x
I saw it not as merely renaming the variables, but as making the substitution in the original equation:
(x2 – 3x + 3)2 – 3(x2 – 3x + 3) + 3 = x \_________/ \_________/ y yThat’s what you were doing, isn’t it? It isn’t clear from the equations alone. This was a good insight.
Now, what I notice here is that the two equations are the equations of a function and its inverse, since the variables are interchanged. And I tend to think graphically, so I pictured the problem now as finding the intersections of the graphs of a function and its inverse. The graphs are reflections of one another in the line y = x. Two such graphs will always intersect along the line y = x (if at all). Why? It’s obvious that if (x, x) is a solution to one equation, it is also a solution of the other, since both equations become the same (x2 – 3x + 3 = x).
However, these are not necessarily the only points of intersection of the two graphs. Draw any parabola and its reflection in the line y = x (that is, any quadratic equation and its inverse relation), and in general you will find that there may be as many as four intersection points.
I didn’t notice until editing this post that this problem is closely related to a problem in an older post, When Can a Function Equal Its Inverse?. There we had to “find \(a\) such that \(f(a)=f^{−1}(a)\).” That is (almost) equivalent to “find \(a\) such that \(f(f(a))=a\),” which is our problem (almost for the same quadratic function \(f\)).
I did not proceed further than this before I saw your follow-up and Doctor Peterson’s response. Now I see that what the book did is closely related to what I was thinking; my four points of intersection suggest a quartic equation, and the two solutions found first correspond to the intersection points on y = x.
I want to show you the graph that I drew just now (I would not have used technology to solve the problem):
Here you can see the two solutions, (x, y) = (1, 1) and (3, 3). You also see something unusual: the two parabolas are tangent at (1, 1). If the blue parabola were shifted slightly (downward, for instance), then the red parabola would shift slightly to the left, and the point of tangency would separate into three distinct points of intersection, one on y = x and the other two slightly off that line. The fact of tangency corresponds to the fact that the quartic equation has a root of multiplicity 3.
Attempting a modified problem
Jitender replied:
Given the graph of two parabolas, shifted 90 degrees apart, by exchange of variables, we find two intersection points rather than four.
I would like to know if using algebra we can express the same.
That would make it quite easy to deduce different conditions.
I wanted to help Jitender discover some of this by himself:
I suggest that you try using the same method to solve the equation
(x2 – 3x + 2)2 – 3(x2 – 3x + 2) + 2 = x.
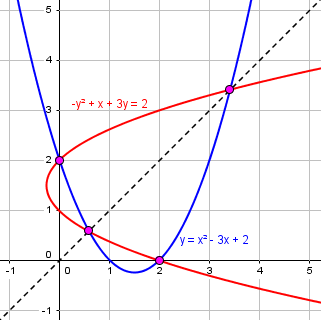
This is an example of the case Doctor Rick described, in which the parabola is shifted down (by one whole unit, rather than just a little), and will nicely illustrate how things will change. All that will be different is that after finding the first two solutions (with y = x), you will find two additional solutions after doing the division. The first two solutions will not be quite as nice, though.
So, yes, it can all be done with algebra.
Jitender wrote back, showing commendable detail in his work on the new problem. See if you can find his errors before I show them:
You have said to decrease constant 3 by 1 to have the equation:
(x2 – 3x + 2)2 – 3(x2 – 3x + 2) + 2 = x.
Attempting that:
(x2 – 3x + 2)(x2 – 3x + 2) = x4 – 6x3 + 13x2 – 12x + 4
I need to take a clue from the book’s solution to get:
x2 – 3x + 2 = x ⇒ x2 – 4x + 2 = 0 ⇒ x= 2±√2
So, I get two solutions, out of a purported 4.
So, the equation
= x4 – 6x3 + 13x2 – 12x + 4, let this be equation (1),
is divisible by (x-2-√2), (x-2+√2); let these roots be denoted by r1 (x = 2+√2), and r2 (x = 2-√2) respectively; and according to the book’s solution, (1) is divisible by product of both r1, r2.
I have a doubt here, as say I first divide (1) by root r1 (wlog), and then the quotient is also divisible by r2 too. Seems I lack some understanding here of polynomial division.
I need to first show if r1, r2 divide (1); and also if the quotient after division by r1 or r2 is divisible by r2, r1 respectively.
x4 – 6x3+ 13x2 – 12x + 4
For r1, (2+√2)4 – 6(2+√2)3 + 13(2+√2)2 – 12(2+√2) + 4
= (68+48√2) – (120-84√2) + (78+52√2) – (24-24√2) + 4
= (146+4-144) + (48+84+52+24)√2
= 6 + 208√2
Doubt 2: This is not 0, so r2 must be wrong too.
Had I been correct in finding r2, r1, next step would have been to pursue further division of (1) by product of r1, r2, i.e. (x2 – 3x + 2).
In case you aren’t familiar with it, “wlog” means “without loss of generality”. It doesn’t matter which root you take first.
He is using some wrong terminology; when he says he is dividing by a root, he really means by the corresponding factor. And what he did at the end is not actually dividing by these factors, but just evaluating; the result would be the same as the remainder of the division, which should be zero. So something went wrong, which I’ll be explaining.
He added,
I want to add that I would very much like graphs, but have learnt that algebraic solution is better and more reliable.
But, for simple cases as my Doubt 1 above, I hope it should be easier to show by graph why decreasing constant by 1 suffices.
We’ll see the graph later.
Correcting the errors
I answered, first about his two solutions, which are correct, though not as “nice” as in the original problem:
I suggested trying this (algebraically) to see that what Doctor Rick said is true in a relatively simple case. Don’t, at this point, think of it as “decreasing constant by 1” (though it should be obvious that that is what I did, and that it is what Doctor Rick suggested in terms of the graph); treat it as a new problem of the same type.
Yes, 2±√2 are our first two solutions, out of a possible 4 for a quartic equation. Now we want to find the other two (which in the original problem were just duplicates of one of the first solutions we had already found, and therefore obscured the idea somewhat).
But your expansion is just part of the polynomial in the equation. You only expanded the product of two factors, and didn’t add the other two terms. This is one cause of your subsequent difficulty.
So he wasn’t working with the correct equation. He was also evaluating the hard way; synthetic division is generally more efficient than “plugging in” the value directly, as we’ll see.
Next, about the equation being divisible:
I’m not sure what you mean when you say “according to the book’s solution, (1) is divisible by product of both r1, r2.” It is not that the polynomial is divisible by the roots, but by the linear factors corresponding to the known solutions. Be careful to distinguish these words.
That is, since we have two zeros of the polynomial x4 – 6x3 + 10x2 – 4x + 0 (which you will get when you correct the expansion), that is divisible by (x-2-√2) and by (x-2+√2). You could do those divisions one at a time; or you could first multiply them and divide by their product (which is what the book said to do). Have you observed that this product is simply x2 – 4x + 2, from which you obtained the roots? (Not x2 – 3x + 2 as you say later — be careful!)
Now do that division. If you have trouble, show us your work.
The factor theorem tells us that if, say, \(p\) and \(q\) are roots of a polynomial \(P(x)\), then \(P(x) = (x-p)(x-q)Q(x)\), where the roots of \(Q(x)\) will also be roots of \(P(x)\). So we can find \(Q(x)\) either by dividing by \((x-p)\) and \((x-q)\) successively, or by dividing all at once by \((x-p)(x-q)\). We’ll do both.
Next, about the work of evaluation itself:
First, you don’t need to do this complicated substitution; just do the division. But the main reason this failed is that, as I said above, you have the wrong quartic.
Synthetic division is often used as a more efficient way to evaluate a polynomial, avoiding the explicit substitution. It’s less convenient when the root is a complex number; by doing long division with the product of the factors, you make the work far easier.
The main benefit of synthetic division as a way of evaluating is that it requires fewer multiplications (which means a lot here, with all those radicals); but also, it gives us the quotient we need! Since, therefore, we need to do the division(s) anyway, we don’t need to do the evaluation another way first. The division proves that the roots are correct.
Finally, on his added question about the use of graphs:
We are not talking about using graphs to solve, but to understand what the algebra is doing. They are extremely useful for that purpose. If someone told you not to use graphs at all (not just for solving), ignore them. But this is exactly why I asked you to solve this problem algebraically, though I had already made a graph for it.
I’ll be showing you the graph for this example when you have solved it, and then you will see what you have done, and how it relates to what Doctor Rick said (which was that subtracting any positive constant would accomplish the goal of changing the problem to have four distinct solutions rather than one with multiplicity 3).
Starting over
Jitender replied:
I took the new system of equations to be:
x2 – 3x + 2 = y,
y2 – 3y + 2 = x
That gave wrong results, as I failed to get correct quartic equation.
I earlier got roots as:
x2 – 3x + 2 = x ⇒ x2 – 4x + 2 = 0 ⇒ x = 2 ±√2
The correct quartic equation is:
(x2 – 3x + 2)2 – 3(x2 – 3x + 2) + 2 = x.
Attempting that:
(x2 – 3x + 2)(x2 – 3x + 2)
(x4 – 6x3 + 13x2 – 12x + 4) – 3(x2 – 3x + 2) + 2 = x
x4 – 6x3+ 10x2 – 3x = x
x4 – 6x3 + 10x2 – 4x = 0. –- (1), eqn. 1
Substituting, or better by synthetic division, to check if x= 2 ±√2 are roots.
The factors are: r1: x = 2+√2, r2: x = 2-√2.
2+√2 | 1 -6 10 -4 2+√2 -6-2√2 4 ________________________ 1 -4+√2 4-2√2 0This shows it is a root, as remainder is 0. Similarly, show for r2, as below.
2-√2 | 1 -6 10 -4 2-√2 -6+2√2 4 ________________________ 1 -4-√2 4+2√2 0I can find the other two roots by dividing: x3 + (-4+√2)x2 + (4-√2)x –(eqn. 2) by r2.
2-√2 | 1 -4+√2 4-√2 2-√2 -4+2√2 ___________________ 1 -2 √2So, I get the equation : x2 – 2x + √2 = 0 —(eqn. 3) after division of (2) by r2.
The roots of quadratic eqn (3) are:
x = (2±√(4-4√2))/2 = 1±√(1-√2)
which is not clear. Better check if I got (3), (2) as correct or not.
Say if (x – r2) (x2 – 2x + √2) = (2), then correct.
(x – 2 +√2 )(x2 – 2x + √2) = (x3 – 2x2 +√2x) + (-2x2 + 4x – 2√2)+
(√2x2 – 2√2x + 2) = x3 +(-4+√2)x2 + (4-√2)x + 2(1-√2)
So, I got a different equation than (2)? Why?
Irrespective of the failure above, I want to ask why book solution states at end:
…usually the number of solutions is doubled in going from f[x] = x, to f[f[x]] = x.
There are a few errors here, though much of the work is good.
Finishing up
I answered:
First, a comment: You don’t need to divide the cubic (2) by each root separately, to show they both work. Dividing by the first, and then dividing the quotient by the second, as you did subsequently, is enough. (Or, as I said last time and will show below, just divide by their product.)
If the quotient is divisible by the second root, then so is the original polynomial.
Second, you omitted the constant term in your first division (of the quartic).
It should be
2+√2 | 1 -6 10 -4 0 | 2+√2 -6-2√2 4 0 ______________________________ 1 -4+√2 4-2√2 0 0So the quotient is x3 +(-4+√2)x2+(4-2√2)x; it appears that you are aware that the quotient is a cubic, though the work doesn’t show it; but you also made a typo in copying it. The latter is the reason for your failure.
Otherwise, the work was good … just this one mistake spoiled the result.
So your last division (of this quotient by the second factor) was wrong.
It should be this:
2-√2 | 1 -4+√2 4-2√2 0 | 2-√2 -4+2√2 0 _______________________ 1 -2 0 0So the remainder is zero as expected, and the quotient is x2 – 2x, leading to the additional roots 0 and 2.
When you don’t get the expected result, check your work!
Dividing by the product
Could we avoid all that work with irrational coefficients? Yes:
What I would have done is long division by (x – 2 + √2)(x – 2 – √2) = x2 – 4x + 2, which as I said is the quadratic from which you got those roots. Here is the division, which avoids the complexity of the radicals:
x2 - 2x + 0 ____________________________ x2 - 4x + 2 ) x4 – 6x3 + 10x2 - 4x + 0 x4 – 4x3 + 2x2 _______________ –2x3 + 8x2 - 4x –2x3 + 8x2 - 4x _________________ 0 + 0Again, we get the same quotient and 0 remainder with less struggle.
Some people do a form of “synthetic division” with higher-degree divisors like this, but I find it awkward.
Here is the graph of this solution, showing the two solutions on the line y = x, and the two that are not:
By shifting the function, we split the triple intersection in the original problem into three.
This example shows that assuming \(y=x\) does not in general yield all the roots, as it did in the book’s problem. Here we can see what happens as we gradually shift back upward:
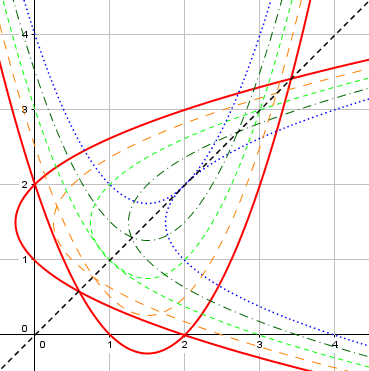
From red to blue, we drop from 4 solutions, to 3, to 2, then to 1; beyond, there would be none.
Finally, about the statement, “…usually the number of solutions is doubled in going from f[x] = x, to f[f[x]] = x.”
I think all he’s saying is that whereas f(x) = x in this example is a quadratic, f(f(x)) = x is a quartic, which typically has four roots; and in general f(f(x)) has twice the degree of f(x). And what we have been doing in our new example is demonstrating that, in fact, it is normal to get four distinct solutions to such a problem. That’s why I wanted you to do this: to gain the experience to see for yourself what he means.
Students often see problems that do not illustrate how “bad” things can get; it’s good to see what’s “normal” sometimes.