Negative x Negative = Positive? Concrete Illustrations

One of the more common questions we’ve been asked is, How can the product of two negative numbers be positive? Between this post and the next, I’ll put together many of the answers we have given, starting here with examples from the “real world” (gradually getting more abstract), and next time we’ll look at proofs.

Do we ever do it in real life?

We’ll start with a question from the very first week of Ask Dr. Math; this page was extended when others asked similar questions, and I’ll include several of those here. From November 1994:

Multiplying Negative by Negative

Dear Dr. Math,

I'm trying to make sense of these rules so that they'll be easier to memorize:

Pos x Pos = Pos, makes sense.  I've been doing it since 3rd grade.  And I can even think of a situation.  I get six birthday cards with $5 in each.

Pos x Neg = Neg, I can think of a situation for this, too.  I get four bills for $20 each so I'd owe money.

But, Neg x Neg = Pos just doesn't make sense.  Does it ever happen in real life?

My teacher said that you could say it would be the opposite of Pos x Neg but that seems like cheating.  It's not realistic.

Thank you,
Sally

The memorizing part is easy: Each negative number in a product changes the sign of the result! So a product with no negatives is positive (the default); one with one negative is negative; one with two negatives is positive; and you can continue when there are more numbers involved. But what does it mean???

Sally’s model is that money is positive, and a bill (requiring payment) is a negative. Multiplication by a positive number means getting the same thing multiple times. How do you multiply by a negative number?

Doctor Margaret answered:

So, one way to think about this is to take 6*(-6) (that is 6 times -6), find the result to this (which is exactly what you have above, ie -36) and then consider what -[6(-6)] is. This is nothing other than the negative of 6(-6) or, if you prefer, its opposite (opposite numbers are two numbers whose sum is 0- you may know this, but I said it just in case you don't know). Clearly, the opposite of -36 is +36, because -36 +36 = 0. Therefore, -6*(-6) = +36

Sally had no trouble with a positive number of positives or negatives; it’s natural that $$6\times(-6) = (-6)+(-6)+(-6)+(-6)+(-6)+(-6)=-36$$ Doctor Margaret didn’t give an example, but used the idea I mentioned above, that changing the sign of a number changes the sign of the answer. More is needed to clarify what it means. Others joined in.

Getting vs sending bills

Doctor Ken said this:

Thanks for the question!  It's great that you want to actually make sense of the situation instead of just doing it by rote.

I'll try to give you an example for the Neg x Neg case, based on your receiving bills thing.

Let's say you got five bills in the mail for seven dollars each.  Then you're right, you'd have 5 x -7 more dollars, i.e. -35 more dollars, i.e. 35 fewer dollars.

But what if you had _sent_out_ five bills instead of getting them?  Then, in a sense, you've gotten negative five bills, so you have -5 x -7 = 35 more dollars than you used to have.

Unfortunately, I can't think of another example right now to really drive the point home.  But I'll keep thinking, and I'll try to get back to you soon! Also, one of the other Math Doctors here might jump in and reply if they think of anything clever.

If I get 5 payments of $6 each, I gain $30: $$5\times 6=30$$

If I get 4 bills for $20 each, I owe $80: $$4\times(-20)=-80$$

If I send someone 5 payments of $6 each, I am $30 poorer: $$5\times(-6)=-30$$

If I send someone 5 bills for $7 each (and they pay), I am $35 richer: $$(-5)\times(-7)=35$$

Is it clear enough that undoing something is equivalent to doing it a negative number of times? Perhaps. I find it hard to keep track of both getting and sending, and money and bills, and being dizzy doesn’t help my understanding!

Taking away a debt

Doctor Steve modified the idea:

Hi Sally, I think you've gotten some good answers and here's another variation, again using your own example with bills.

Neg x Neg: Imagine that you buy five gift certificates worth $5 each and you pay for them using your credit card.  As you point out, you now owe money, so that's -$25.  The bill comes from the credit card company, but I TAKE IT AWAY from you and insist on paying it.  You now have $25 of gift certificates without having paid anything.  Taking away a debt is analogous to negating a negative.  Take away five debts of $5 (-5*-5) equals a gain of $25.

Here, instead of sending a bill, we are having a bill paid for us; removing a negative is the same as adding a positive.

Walking backward, facing backward

A year and a half later, a reader named Tom added another:

My son found the debt metaphor pretty helpful.  I have since been told about one I like even better.  Imagine a number line on which you walk. Multiplying x*y is taking x steps, each of size y.  Negative steps require you to face the negative end of the line before you start walking and negative step sizes are backward (i.e., heel first) steps.  So, -x*-y means to stand on zero, face in the negative direction, and then take x backward steps, each of size y.

Here, each step is \(+2\), moving two units to the right; he is taking \(3\) steps (\(3\times 2=6\)), or \(-3\) steps (\((-3)\times 2=-6\)), meaning that he “untakes” the steps:

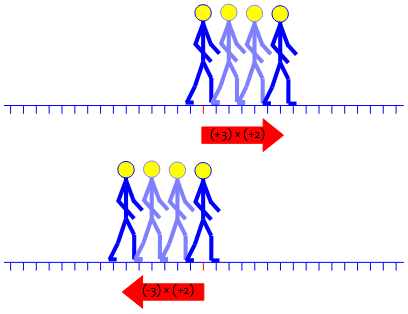
Here, each step is \(-2\), moving two units to the left; he is taking \(3\) steps (\(3\times(-2)=-6\)), or \(-3\) steps (\((-3)\times(-2)=6\)), meaning that he “untakes” the steps:

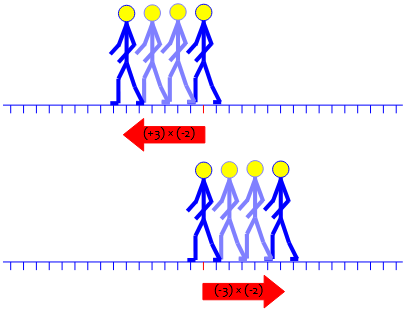
In the last case, we are taking a negative number of negative steps, and moving forward.

Motion past and future, east and west

In 1998, Doctor Pete answered a question similarly, but going backward in time rather than walking backward:

Imagine the following situation:

You're standing at a street corner. At exactly noon, a car passes by you, going east, at a constant rate of 20 miles/hour. After one hour has elapsed, that is, at 1:00 p.m., it would be 20 miles east of where you're standing. And one hour ago, at 11:00 a.m., it was 20 miles west of where you're standing.

Now, what would it mean if the car was travelling east at -20 miles/hour? It'd be in reverse, going west, of course. So, if it were going at -20 miles/hour east, at 1:00 p.m. it would be 20 miles west of where you're standing. Finally, if it were going -20 miles/hour east, at 11:00 a.m., where would it be? 20 miles east, of course. What does this mean?

     (-20 miles/hour)(-1 hour) = 20 miles.

Hence here is a "concrete" explanation of why two negatives multiply to make a positive number.

Distance equals rate times time, and both rate and time can be negative, at least in calculations. If you are going 20 miles per hour to the west (\(-20\) mph “east”), then 3 hours ago (\(-3\) hours of driving), your position was \((-20)\times(-3)=+60\) miles east.

Motion in the past: more detail

Another 1998 question was put in a separate page:

A Negative Times a Negative

Hello Dr. Math,

I would like to know more about integers. My question is, why do you have to take out the negative sign when you multiply two negative numbers (i.e. -2 x -2 = 4)?

Thank You,
El-ad Blech

In other words, why does \(-2\) change to positive when multiplied by \(-2\)?

I answered:

Hi, El-ad, 

This is something a lot of people have trouble understanding. I'll give you an explanation I find helpful.

One thing that helps is to realize that negative numbers are just an extension of the number line, and when we try to decide how to do operations on them, our main concern is to keep everything working the way it does when you work with positive numbers.

This will be a key idea when we look at proofs next time. When we invent a new kind of number, we have to define the operations in a way that will still be compatible with the operations we know and love. Here, we’ll do that not in the abstract (as we will next week), but in terms of one application of multiplication: rate problems such as we’ve just been considering. But this time, we’ll see them in terms of graphs.

Suppose I make a graph of a line; maybe it represents how far I travel if I keep going forward at a constant speed, so the horizontal axis is time and the vertical axis is distance (or position along a road):

     D
     |         / 
   6 +       X
     |     /
   3 +   X
     | /
   0 +---+---+---+ T
     0   1   2

This graph shows that I went 3 miles in the first hour, and another 3 in the second hour, so in two hours, I went forward 2 * 3 = 6 miles. I can represent the graph by the equation:

   D = 3 * T

More generally, we say “distance = rate × time”, or \(d=rt\). To keep numbers small, I used a speed that’s slow even for walking! $$3\times 2=6$$

I can continue this graph backward in time, to figure out where I would have been at earlier times. If I do that, it should still follow the same rules as for positive times. As I go from right to left on the graph above, D decreases by 3 each time I decrease T by 1. It should still do that if I continue it for negative values of T, so it will look like this:

               D
               |         /
             6 +       X
               |     /
             3 +   X
               | /
   +---+---+---+---+---+---+ T
      -2  -1 / |   1   2
           X   + -3
         /     |
       X       + -6
     /         |

So for T = -2, D = 3 * (-2) = -6. That part isn't hard to believe. All we're doing is continuing the straight line to the left. In terms of motion, at a time before the present I was at a place behind my starting point.

The reasoning here is similar to something we’ll see later involving “patterns”. It is not surprising that negative times (at positive speeds) yield negative distances, and that multiplying a positive rate and a negative time gives a negative distance. $$3\times (-2)=-6$$

Now let's think about negative speeds. Suppose I'm driving backwards (maybe the wrong way down a one-way street, or with my car in reverse). Then for each hour I drive, I go -3 miles, that is, 3 miles backward:

               D
               |     
             6 +    
               |   
             3 +  
               | 
               +---+---+---+ T
               | \ 1   2
            -3 +   X
               |     \
            -6 +       X
               |         \
This represents the equation:

    D = (-3) * T

If I go backward for a positive time, I’m multiplying a negative speed by a positive time, and it makes sense that I end up behind where I started. $$(-3)\times 2=-6$$

How do I continue this for negative times? Since D increases by 3 each time T decreases by 1, it should look like this, continuing the straight line backwards:

               D
     \         |
       X      6+
         \     |
           X  3+
             \ |
   +---+---+---+---+---+---+ T
      -2  -1   | \ 1   2
             -3+   X
               |     \
             -6+       X
               |         \

But that means that at time T = -2,

    D = (-3) * (-2) = 6

This is where people usually start to question the result; but both the graph, and the image of moving backward, should make it clear: If I walk backward, then in the past I was ahead of where I start. $$(-3)\times (-2)=6$$

What all this really means is just that a negative sign on either factor reverses the result, and reversing it twice makes it positive again.

I hope that helps make it more visible.

This, to me, is the main idea.

Tables and tapes

Yet another question came in 1998:

Negative Times Negative

Could you provide an example for comprehending how a negative times a negative is a positive? - maybe on the number line. I would like to understand it rather than just take it as fact.

Wanting to understand is exactly what we like to see!

Patterns in the multiplication table

Doctor Gail answered in two ways, first with the pattern that I mentioned a moment ago:

Dear Julia,

Here are a couple of examples for you:

If you are convinced that a positive times a negative is negative, then one way to look at negative times negative is to observe a pattern.  Consider the following:  

     3x(-3) = -9
     2x(-3) = -6
     1x(-3) = -3
     0x(-3) =  0

so what comes next in the pattern?  Notice that in each case we are multiplying -3 by a number 1 smaller than the previous number. Also observe the pattern that is being created with the products. So the next logical multiplication sentence is 

  (-1)x(-3) = 3

Note that negative times negative was positive.

This is the same idea as continuing the lines backward in the rate example we just saw.

Playing the tape backward

Then she gave her own version of the rate example:

One of the best realistic interpretations that I have found concerns videotaping. Consider videotaping two students, Julia who is walking forward in the tape and holds a sign saying "I am walking forward."  Also consider her friend who is walking backward in the tape and holds a sign saying "I am walking backward."  Now playing the tapes in the normal fashion would be forward times forward or positive times positive and Julia looks like she is walking forward (the result is positive). Similarly, the meaning of negative times negative might be interpreted as viewing "rewind" times "the friend" or backward times backward. What would it look like the friend was actually doing?  Walking forward! So one can visualize backward times backward is forward or negative times negative equals positive.

I hope this explanations begin to convince you that negative times negative equals positive.

You could generalize this, and make it clearer that multiplication is involved, by observing that in playback you can play at double speed (multiplying the motion by 2), or at half speed (multiplying by \(\frac{1}{2}\); or reverse (multiplying by \(-1\)), or reverse at double speed (multiplying by \(-2\)), and so on.

Julia replied,

What a most unusual example for visualizing a negative times a negative - the videotaped example.

I am actually going to try it since I do video training tapes. Thanks ever so much.

It could be nice to see a set of such videos; has anyone made some?

Geometrical multiplication

I’ll add one more, from 2006:

Modeling Multiplying Two Negatives with Number Lines

I'm trying to use a number line to figure out why -2 times -3 makes 6, and I can't do it.  If I start at -2 and move to the right three times I wind up at 4, and if I move to the left I wind up at -8.

What is the logic behind the rule of a negative times a negative makes a positive, and how do I demonstrate it on a number line?

What does multiplication look like on a number line? That leads to a unique approach from Doctor Rick: a method for multiplying numbers geometrically using similar triangles:

Hi, Joan.

You can find a variety of ways to think about multiplication of negatives, and also ways to *prove*, more or less formally, that a negative times a negative is positive, in the Dr. Math FAQ:

  Negative X Negative = Positive
  http://mathforum.org/dr.math/faq/faq.negxneg.html 

It's hard to demonstrate signed multiplication on a number line, but there is a way to do it using *two* number lines.  See what you think of this:

(The FAQ contains much of what we’ve seen above.)

Draw two number lines that cross at the origin on both lines--the angle between the lines doesn't matter.  To multiply a number x by another number y, first draw a line through 1 on the first line and x on the second line:

               /
              /
             /
            /
           /
        x /
         *
        /
       /
      /
  ---0--*-----------
    /   1
   /
  /

I can't draw that line, you'll have to do it on paper.

From here on, I’ll replace his drawings with better ones. Here is the first:

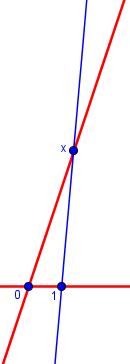
Then draw another line, parallel to this one and passing through the number y on the first number line.

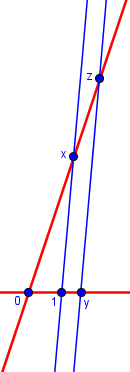
You can easily prove by similar triangles that 

  x/1 = z/y

so that

  z = xy

That is, the position of z on the second number line is the product of x and y.

That’s a well-known procedure for multiplying numbers, and is simple enough for positive numbers. We could try positive times negative, as in the last couple explanations, but he jumps straight to negative times negative:

Now, use this same graphical method to multiply -2 by -3:

Draw a line connecting 1 on the first (horizontal) number line with -2 on the second number line.  Draw a line parallel to this line, and passing through -3 on the first number line.  You will see that it intersects the second number line at 6, which is therefore the product of -2 and -3.

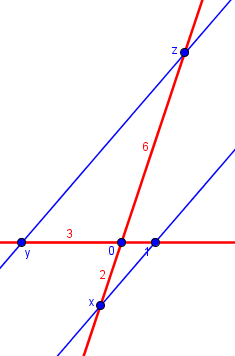
Here x is at \(-2\), y is at \(-3\), and z is at \(x\times y=-2\times-3=+6\).

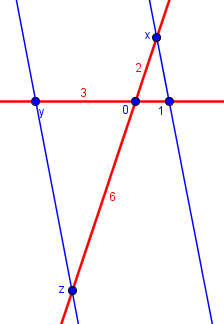
Just for fun, let’s also multiply \(x\times y=2\times-3=-6\):

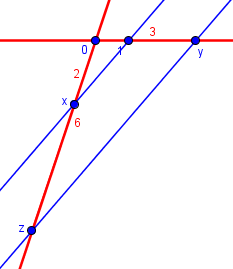
and \(x\times y=-2\times 3=-6\):