(New Question of the Week)
This week I answered a seemingly simple question that can be solved in several different ways when presented as multiple choice, but is rather difficult as a straightforward algebra problem. Trying to guess what the “patient” had done yielded an invalid method that gave the right answer — or was it really invalid? Luckily, something about it seemed familiar, and I found the answer in a question from last year, which itself had a complicated history! The result is worth sharing.
The problem
Here is the question, from Sinan:
The problem is:
If \(f:\left(-\infty, \frac{3}{2}\right] \mapsto \left[-\frac{29}{4}, +\infty\right)\) is defined by \(f\left(x\right) = x^2 – 3x – 5\), find a such that \(f\left(a\right) = f^{-1}\left(a\right)\).
A) 1 B) 1/2 C) -1 D) -3/2 E) 5
I found the inverse function and by the equation found the answer as 5. But 5 is not a desired answer according to the information given.
In case you are unfamiliar with the notation, this defines a quadratic function, restricting its domain to the left of its axis of symmetry \(\left( x = \frac{3}{2} \right)\); this makes it one-to-one, so that it has an inverse function. We are required to find values of x for which the value of the function equals the value of the inverse function. He got 5 as an answer, which is not in the specified domain, so he wondered if there really was no solution.
My initial response was to ask for details of his work, but in the mean time I suggested a possible error he might have made (which in fact he didn’t), and indicated both the direct method (which turned out to be what Sinan had done), and an easier method by which I got the correct answer:
As always, my first response is, please show how you got 5 as an answer! Just telling us what wrong answer you got doesn’t help us help you.
Now, I suspect you may have misread the question. It is possible that you solved \(f\left(x\right) = x\), that is, \(x^2 – 3x – 5 = x\), which finds a value of a such that \(f\left(a\right) = a\), not \(f^{-1}\left(a\right)\). But you say you found the inverse, so this seems unlikely; and you should have found two solutions, one in the required domain. So I can’t tell what mistake you might have made. Please show some details.
The direct way to solve would be to find an expression for \(f^{-1}\left(x\right)\) and solve \(f\left(x\right) = f^{-1}\left(x\right)\). What I did instead, saving the work of finding the inverse, was to apply \(f\) to both sides, so that \(f\left(f\left(x\right)\right) = f\left(f^-1\left(x\right)\right) = x\). So I found an expression for \(f\left(f\left(x\right)\right)\) and solved \(f\left(f\left(x\right)\right) = x\). This gave me a fourth degree equation, which would be unpleasant, except that using the rational root theorem, together with the list of choices, I only had to check three possibilities (by synthetic division).
Does that give you enough ideas?
Sinan responded by showing his attempt to follow my suggestion, together with what he had first done:
Yes by your method the answer is -1.
\(x = y\)
\(x = x^2 – 3x -5 \Rightarrow x = -1\)Here is my wrong solution:
\(f\left(x\right) = x^2 – 3x – 5\)
\(f\left(x\right) = \left( x – \frac{3}{2}\right)^2 – \frac{29}{4}\)
\(f^{-1}\left(x\right) = \sqrt{x + \frac{29}{4}} + \frac{3}{2}\)
\(\left( x – \frac{3}{2}\right)^2 – \frac{29}{4} = \sqrt{x + \frac{29}{4}} + \frac{3}{2}\)I tried the five choices, one by one. When I chose \(x = -1\), \(f\left(x\right) \ne f^{-1}\left(x\right)\).
It turned out that his original work was not what I thought, but was close to being correct; he took the “direct way” I’d described, but in finding the inverse, he neglected to choose the negative sign on the radical due to the fact that the domain of f was restricted to the left side of the parabola. Then he checked each of the five choices. The only reason I didn’t do this was my bias against using given choices by trial and error rather than actually solving the problem mathematically. (I don’t like to assume that the choices include all correct answers.) But what he did was undoubtedly the easiest way to solve it, given that it is a multiple-choice problem.
His equation should have been:
\(\left( x – \frac{3}{2}\right)^2 – \frac{29}{4} = \frac{3}{2} – \sqrt{x + \frac{29}{4}} \)
Solving this radical equation algebraically yields the same quartic equation I got using \(f\left(f\left(x\right)\right) = x\), namely \(x^4-6x^3-4x^2+38x+35 = 0\). The rational root theorem leads us to try -1 and 5, and the result lets us find the other two solutions, \(1 \pm 2\sqrt{2}\). Of these four solutions, only the first satisfies the original problem.
Sinan didn’t do all that, since it is a multiple-choice question; just checked the given choices, and found that -1 is the one that works:
LHS: \(\left( -1 – \frac{3}{2}\right)^2 – \frac{29}{4} = \left( – \frac{5}{2}\right)^2 – \frac{29}{4} = -1\)
RHS: \(\frac{3}{2} – \sqrt{-1 + \frac{29}{4}} = \frac{3}{2} – \sqrt{ \frac{25}{4}} = -1\)
Note an interesting fact here: both sides of the equation happen to equal x itself. This will be important!
The wrong way – or is it?
But in his attempt to do what I said, he instead did what I said not to do. So after explaining what I just showed, I continued:
Your new work is not the work I said to do; it is what I said you might have done, which is technically wrong: “It is possible that you solved \(f\left(x\right) = x\), that is, \(x^2 – 3x – 5 = x\), which finds a value of a such that \(f\left(a\right) = a\), not \(f^{-1}\left(a\right)\). ” That is not what you were asked to do.
I considered saying that this is a poorly written problem, because taking an unjustified shortcut like this happens to give the right answer, but I chose not to reveal that.
But I was getting curious: the “invalid shortcut” I had initially assumed Sinan had used by misreading the problem actually gave the correct solution; could it really be valid? I wanted to be sure. Examining the graph of the function and its inverse, I saw the fact that the solution lies on the line \(y = x\):
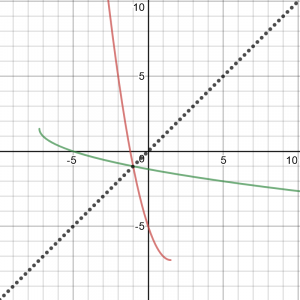
If that is always going to be true, then it will be valid to solve \(f\left(x\right) = x\) rather than \(f\left(x\right) = f^{-1}\left(x\right)\).
But when I had initially graphed the functions, I had not taken the trouble to include the domain restriction; I had seen this:
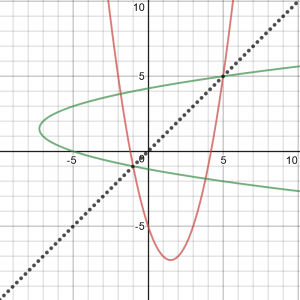
Here we see four intersections, only two of which lie on \(y = x\). (One of those, by the way, is the wrong solution Sinan had first found, by taking the wrong part of the inverse function.) But on closer inspection, the two other intersections are not between a function and its own inverse, but between the positive half of one relation and the negative half of the other.
I tried a couple more functions, and the same thing happened. So I was wondering it my shortcut were actually valid. I wouldn’t want to call a valid method invalid. Maybe the conjecture is true as long as we are talking about a one-to-one function and its inverse …
The truth (and a few errors)
But then I realized that this question seemed familiar, and vaguely recalled that the answer involved functions that were monotonically decreasing. Searching my records, I found the following (unarchived) answer from October, referring back to a previous unarchived answer that had been wrong. This is getting complicated!
Question [10/14/2017, from Fida]: I did a bit of experimenting and I came to the conclusion f(x)=f^-1(x) if there is a solution, then the point of intersection lies on the line y=x Answer: Actually, it is NOT true that the point of intersection must have y=x! It is easy to convince oneself (short of an actual proof) that it should be so, but here is one counterexample: f(x) = -x^3 f^-1(x) = -x^(1/3) f(x) = f^-1(x) ==> -x^3 = -x^(1/3) x^3 = x^(1/3) (x^3)^3 = (x^(1/3))^3 x^9 = x x^9 - x = 0 x(x^8 - 1) = 0 x = 0 or x = 1 or x = -1 y = 0 y = -1 y = 1 So there are three real solutions, but only one of them lies on the line y=x. You can see what is going on when you graph the two functions; the intersection points are reflections of one another. It is VERY easy to come to the wrong conclusion; looking back, I see at least two places where Math Doctors in the past have agreed with you. Here is a question and answer from 9 years ago about this, referring to an answer given the previous year that was not archived, but was posted by its recipient on a Greek discussion group, in support of one person's belief about the problem:
Question [6/25/2008, from Nikos]:
Suppose that f is an invertible real function of one variable. It is known that the graphs of f and f^{-1} are symmetric with respect to the line y=x. It is also known that if f is increasing then the common points of f and f^{-1} (if there exists) are on the line y=x.
My question is: What can we say when f is decreasing? The intersections of f and f^{-1} only lie on the y=x or is it possible to meet at points not belonging on the y=x? Example f(x)=-x^3.
I am a mathematician but I really want your help. In my opinion the graphs of f(x)=-x^3 and its inverse meet at 3 points. (-1,1) (0,0) (1,-1). But I get confused when I read at http://forum.math.uoa.gr/viewtopic.php?t=984&sid=865caa471f0db868f5826a68b1d1dcd2 the following:
Question [11/16/2006, from Bilstef]: Let function f, which is invertible. Then which are the points where f and f^-1 meet? How do we find them? By solving only the f(x)=x? What happen if f is increasing and what if decreasing? Are the meeting points only on the line y=x? Answer: Hello, You're correct, the place where a function and its inverse intersect must always be on the line y = x. Do you understand why? Please write back if you would like an explanation. - Doctor Gaff, The Math Forum
thank you in advance Nikos Fotiades Answer: We put answers we think are worth sharing with others in our archives; sometimes people write to us when they find an error there, and we correct it. We are only human, and are grateful when we are corrected. Evidently this answer, which we did not archive, was posted on a site we do not control, so we can't correct it. That is unfortunate. This is simply a wrong answer, and we have since answered the same question more correctly when others asked something similar. It is not true that a function can only intersect its inverse on the line y=x, and your example of f(x) = -x^3 demonstrates that. There are many others, of course; these include functions that are their own inverse, such as f(x) = c/x or f(x) = c - x, and more interesting cases like f(x) = 2 ln(5-x). The correct statement is that f will intersect f^-1 at any x for which f(x) = x, but may intersect in other places as well. I presume you have a proof that a monotonically increasing function can intersect its inverse only on y=x; I don't think that is hard to prove. Clearly, it is not true for a decreasing function. A mathematician knows not to trust what anyone says without proof; your counterexample shows that he can't have a proof, so you can ignore (or correct) that hastily made claim. - Doctor Peterson, The Math Forum
Here is the subsequent answer I referred to; I later realized that it appears to be the same “Bilstef” under a different name, so we had given him both the wrong, and then the correct, answer:
Question [12/2/2007, by Vasilis]: let f(x) = - x^3+1 then f^-1(x)= (1-x)^(1/3).were do their graphs intersects Are their graph intersect only on the y=x and why? Their graphs thru Graphmatica programme show that they intersect also in (0,1) and (1,0). Is that correct? Why? How do we find where the graph of f and f^-1 intersect? Answer: Hi, vasilis -- The graphs of any function and its inverse will intersect on the line y=x. But the graphs can intersect in other places also. In your example, the two graphs intersect on the line y=x and also at (0,1) and (1,0). - Doctor Greenie, The Math Forum <http://mathforum.org/dr.math/>
Finishing the answer to Fida:
Both Dr Gaff and Bilstef subsequently attempted to prove that y=x, but both proofs have major gaps. Both undoubtedly tried to visualize intersecting graphs and thought they saw an impossibility, so that they didn't think they had to be careful with their proofs, because it seemed obvious. Clearly, this is a tricky problem! What is happening is that f(x) = f^-1(x) will be true for any x such that f(x) = x; but more generally it is true whenever f(f(x)) = x as you can see by applying f to both sides of the original equation. For this, it is not necessary that f(x) itself be x.
As you can see, Doctor Gaff misspoke; Doctor Greenie then recognized the correct answer; then I was almost convinced but realized my error. This illustrates why mathematicians don’t like to speak off the cuff and say something they think is right but haven’t proved. This is also why I took the time to pursue this question, having actually written and then deleted comments that suggested the “shortcut” might be right.
To tie up a loose end, here is the graph of the classic counterexample:
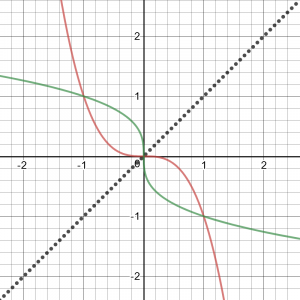
Clearly, the solutions of \(f\left(x\right) = f^{-1}\left(x\right)\) are not the solutions of \(f\left(x\right) = x\). So I was right: we can’t use the latter to solve the former (unless f is an increasing function).
