Last week we looked at some basics about zero; now let’s look at whether zero is positive or negative, and then at the topic of the recent comment that triggered this series: whether zero is even or odd.
Positive, negative, or neither?
We’ll start with a question from 1995:
Why Zero is neither Positive nor Negative Dear Dr. Math, My class and I are wondering if 0 is a negative or a positive number and why. My name is David and I am in fifth grade at Kyrene De La Sierra in Phoenix. Sincerely, Ms. Kieselbach's class
Doctor Ken answered:
Hello! Actually, zero is neither a negative or a positive number. The whole idea of positive and negative is defined in terms of zero. Negative numbers are numbers that are smaller than zero, and positive numbers are numbers that are bigger than zero. Since zero isn't bigger or smaller than itself (just like you're not older than yourself, or taller than yourself), zero is neither positive nor negative.
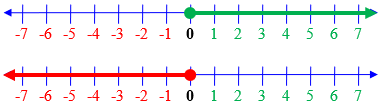
Zero is the dividing point, and is not on either side of the line. Here, positive numbers are green, negative numbers are red, and zero is neither:
![]()
People sometimes talk about the "non-negative" numbers, and what that means is all the numbers that aren't negative, in other words all the positive numbers and zero. So the only difference between the set of positive numbers and the set of non-negative numbers is that zero isn't in the first set, but it is in the second. Similarly, the "non-positive" numbers are the negative numbers together with zero.
It is easy to say “positive” when you really mean “non-negative”, because you forgot to think about whether to include zero! Here are the non-negative numbers:

Here are the non-positive numbers:

We previously discussed this in Talking About Negative Numbers.
Technically, if we’re talking about real numbers and not just integers, these should be:
Even or odd?
Now let’s turn to the question of “parity” (oddness or evenness), with a question from 1998:
Is Zero Odd or Even? Is zero odd or even? My 4th grade students are not satisfied with any explanation I can offer. Zero after any other number is even because it can be divided by 2. It holds an even place in the number line. Is it just special the way that 1 is neither prime nor composite?
(We discussed 1 not being prime or composite in Prime Numbers: What About 0 and 1?)
Wendy knows that zero is even, but can’t convince her students! Her first argument appears to be that since we can decide whether a number is even by whether its units digit is even (e.g. 36 is even because 6 is even), and all numbers that end with the digit 0 are even (e.g. 30 is even, and it ends in zero), then for consistency, 0 itself must be even. Not bad! And every other number on the number line is even, so we can’t skip over the place where zero is. Look back at that number line:
![]()
(Not sure about those negative numbers? We’ll get there!)
If we didn’t call zero even, it would look like this:
![]()
Something looks wrong, doesn’t it?
But since zero was special in terms of sign, maybe it’s special here, too?
Doctor Mateo answered, focusing on the definition:
Hello Wendy, You are right. Zero is an even number. An even number is a number that is exactly divisible by 2. That means that when you divide by two the remainder is zero. You may want to review the multiplication facts for 2: 2 x 0 = 2 x 1 = 2 x 2 = 2 x 3 = and so on. After writing these number facts out or reviewing them with the class you can ask them about patterns and eventually tell them that this is how they can create a list of even numbers.
Ultimately, we just have to go to the definition. We can (equivalently) say either that an even number is one that is exactly divisible by 2, or one that is a multiple of 2. So all the numbers in the list of multiples are the even numbers: 0, 2, 4, 6, … .
Then have them divide several numbers by 2 (including 0) and let them see a second way to conclude that a number is even (the remainder of the evens is 0 and the remainder of the odds is 1). Later when the number system is expanded to include the set of integers, they will be able to carry the concept over without much difficulty.
We’ll be looking at this extension below.
For more on integers, see the Dr. Math FAQ: "Integers are the whole numbers, negative whole numbers, and zero... The terms even and odd only apply to integers; 2.5 is neither even nor odd. Zero, on the other hand, is even since it is 2 times some integer: it's 2 times 0." http://mathforum.org/dr.math/faq/faq.integers.html
But can you really divide zero by 2?
A 2001 question takes us a little deeper:
Is Zero Even? At numerous sites across the Internet the answer to the question whether zero is odd or even seems to be totally subjective, and the proofs used to justify 'even' (zero can be divided by two, therefore it is even), sound reasonable. But zero can't really be divided by two since the result is zero - neither a positive or negative integer. Q: How many times does 2 go into 0? A: Zero times. Or to rephrase, two doesn't go into zero. Thanks.
Last time we saw how some people question the idea of multiplying, say, 2 by zero to get zero. Can you really divide zero by 2?
Doctor Rick answered:
Hi, John. Thanks for writing! I hope I can clear up some confusion. Our archives sometimes say that zero is neither positive nor negative, not that it is neither even nor odd. That's very different.
If there is “subjective” debate about this online, it is not by knowledgeable people!
The question of evenness or oddness is based on definitions. There may be variations on how "even" is defined, just as there are on how "natural numbers" are defined; but once you have established your definition, the question can be answered objectively based on that definition. An even number, as our archive pages say, is defined as one that is divisible by 2. Divisibility by 2 is defined as giving an integer quotient when divided by 2. The only matter open to debate is whether this last statement should say "integer," "natural number," or "whole number." If integer, then the even numbers are ..., -6, -4, -2, 0, 2, 4, 6, ... If natural number (0, 1, 2, 3, ...), then the even numbers are 0, 2, 4, 6, ... If whole number (1, 2, 3, ...), then the even numbers are 2, 4, 6, ...
The variation in definition of “natural numbers” is about whether to include zero or not, and affect words, not math.
The question here is whether there is reason to extend the definition of “even” beyond the positive integers, or reason not to do so.
There is no reason to be restrictive in our definition of divisibility: the definition introduces no contradictions or special cases when it is extended to all integers. If you have found places on the Web where a restrictive definition is used, I'd like to see them. You state that the problem you have with zero being even is that zero can't really be divided by 2, because the quotient is 0, which is neither positive nor negative. Putting this in my terms, you are defining "divisible" as meaning "giving a quotient that is a positive or negative (that is, non-zero) integer." I could accept one of the alternative definitions I gave above before I would accept yours.
It isn’t clear why John might think a quotient of zero is not allowed; it may be related to the arguments against multiplying by zero that we saw last time.
If we say that zero cannot be divided by anything, then this introduces lots of special cases to our mathematical properties. For example, the sum of two even numbers is even. You are telling me that the 4 and -4 are even, but that the sum of 4 and -4 is *not* even. We'd need to change the rule to "The sum of even numbers is even, UNLESS it is zero." It's so much simpler to define our terms in a way that does not require such special cases. Defining evenness and divisibility as we do does not introduce special cases.
This is one very important reason for making sure that we do call zero even: We make definitions so that they will be useful, as we saw recently with polynomials.
Before zero was introduced to our number system, negative quantities were treated as an entirely separate kind of entity from positive numbers. Different rules were needed for lots of different cases, depending on whether a quantity was added (positive) or subtracted (negative). The history of quadratic equations illustrates this. A big part of the genius of introducing zero in the first place was that it unified all these special cases into one. I am asking you now to see that you do not need to treat zero as special; and when you treat it like every other integer, it follows that zero is even.
We saw the value of signed numbers in avoiding special cases in How Real Are Negative Numbers?
Can negative numbers be even or odd?
Let’s take the even/odd question one step further, combining all the ideas we’ve seen, with this question from 2006:
Can Even and Odd Numbers Be Negative? Can even or odd numbers be non-positive? For example, is 0 even? Is -4 even? Is -5 odd? Some teachers say that even and odd numbers do not include negative integers, but some teachers say they are included.
Doctor Rick answered:
Hi, Sarah. No problem arises when the definition of even and odd is extended from the positive integers to all integers, so I see no reason not to do so. An even number is an integer that is divisible by 2 (that is, it can be written as 2 times some integer); an odd number is an integer that is not divisible by 2.
Generalization is good; if you can extend a concept without causing harm, do it!
In contrast, if we try to extend the concept to non-integer rational numbers, we encounter difficulties; any definition that is self-consistent is not particularly useful. Therefore we restrict evenness and oddness to integers; the number 1/2 is neither even nor odd.
The question whether a fraction can be called even is discussed at length in Kids Ask About Even and Odd Numbers. That will show what “self-consistent but not useful” means.
I'd like to hear the reasons that those teachers give for not including negative integers. This question comes up a lot (usually in the form "is zero even, odd, or neutral?"), and I have yet to see a good reason.
Sarah replied,
Some teachers say that we only need the concept of even and odd numbers when we count. It is meaningless to extend our discussion of even and odd to non-positive integers. Are these teachers right? What is the use of extending the discussion of evenness and oddness to non-positive integers?
Doctor Rick responded:
Hi, Sarah. I think we must distinguish between "meaningless" and "useless". Extending the definition of evenness and oddness to non-positive integers is not meaningless, because it is self-consistent; as long as a definition doesn't break anything, it imparts meaning "by definition". "Useless," on the other hand, is a word that pure mathematicians don't care for; many mathematical concepts were developed without thought of whether they had any use, but often applications of the concepts have appeared long afterward.
I would say that the “use” of identifying negative even numbers is to maintain rules such as that the difference of two even numbers is even. Stopping any property at zero seems likely to mess up something.
The terms "even" and "odd" do have their origin in counting: if you count 22 objects into two piles, the piles are the same size (even), whereas if you count 23 objects into two piles, you get one left over (odd). The most frequent usage of the words "even" and "odd" is certainly in the domain of non-negative integers. (I want to include 0 as an even number, because if you have no apples and you divide them between two people, you don't have any apples left over.)
Although we normally think of counting a positive number of objects, the extension to zero is so natural as to hardly feel like an extension at all (now!).
I could point out other ways in which mathematicians use the words "even" and "odd", without reference to numbers at all: there are even and odd functions and even and odd permutations. Both grow out of the non-negative-integer sense of even and odd: a polynomial consisting of only even powers of the variable (including 0) is even; a permutation that can be expressed as a product of an even number of transpositions (including no transpositions) is even.
The polynomial \(3x^4-5x^2+7\) is even because all its exponents are even (including the “invisible” exponent 0 on the constant term – see Polynomials: A Matter of Degrees).
The permutation that takes (1, 2, 3, 4) to (3, 2, 4, 1) is even because we can take 2 steps, changing (1, 2, 3, 4) to (3, 2, 1, 4) by interchanging 1 and 3, and then changing that to (3, 2, 4, 1) by interchanging 1 and 4.
My principal difficulty with those who ask, "Is -2 an even number?" and answer "no", is that once a negative integer is brought into the discussion, there is no reason to say it isn't even or odd. The only reason to restrict the even and odd numbers to positive integers is when no other numbers are in view; for instance, when counting or when factoring numbers. Then, even numbers mean *positive* even numbers, simply because positive numbers are the only numbers that exist, for the present purpose. But when you ask about a negative number, it is natural to apply the definition to that domain: an even integer is one that can be expressed as the product of 2 with some integer (not only a positive integer). What would be gained by saying that there are three classes of integers: even integers, odd integers, and negative integers?
So although “even” originally was applied only to whole numbers because no one had thought of asking the question about other numbers, as soon as you do ask the question of negative numbers, you find that the same definition applies.
One interesting thing about the even integers is that this set is closed under addition and multiplication: if you add two even integers, you get an even integer, and if you multiply two even integers, you get an even integer. The set of even integers is thus a useful example in abstract algebra. Looking through my abstract algebra textbook, I find this: "Let E = {even integers} = {2n | n is in Z}. Then (E, +, *} is an infinite commutative ring without identity where + and * are ordinary addition and multiplication." There is one example of mathematicians applying the term "even" to all integers, and also one demonstration of the usefulness of the concept to mathematicians. The set of even integers is interesting. To me, that is sufficient justification.
Definitions typically are what they are in order to be useful, interesting, or both.
Comments on the evenness of zero
Here is the relevant part of a comment on the post about 0/0, that led me to write about this topic:
… More than that, I do consider number 0 parity undefined, because when checking number 0 parity, dividing \(\frac{0}{2}\), even if the remainder is 0, because the quotient is 0, that means that number 0 parity is undefined.
Here some logical contradictions arise when considering 0 even number, because we check number parity dividing absolute value number by smallest even absolute value number, if 0 is even, it is automatically smallest even absolute value number, therefore we must divide by 0 instead of 2. Contradiction.
I answered, in part:
… your comments about parity (even/odd) make no sense to me; you seem to be starting from a wrong definition. A number is even when it can be obtained by multiplying an integer by 2; there is no need to talk about division, much less to reject a quotient of 0. If someone has said that we have to divide by the smallest absolute value of an even number, they must have had only positive integers in view; that statement is easily corrected by saying that an even number is a multiple of the smallest even positive integer. (But why would you use the word “even” in its own definition?) Do you have a source for your definition?
He responded,
**Definition:**
Numbers parity is counting number of units or object if they are odd or even.
Zero has no units or objects, therefore number zero parity is undefined.**Demonstration:**
3: 🍏🍏🍏
2: 🍏🍏
1: 🍏
0: zero apples, therefore zero parity is undefined
I replied,
But your “definition” is not the real definition (I asked for a source!); it is not even a definition at all, since it uses the word “even” without defining it. All you are doing is stating your own idea about what “even” should mean.
I followed this with some proper definitions, and added:
There is a reason for preferring a definition that includes zero; it makes many rules (such as that the sum of two even numbers is even) consistently true, and it eliminates what, by your “definition”, would be a gap in the list. In general, mathematicians prefer such inclusive definitions, rather than arbitrarily excluding special cases as you want to do.

10 = (2, 2, 2, 2, 2), 5 groups of 2 elements with no remainder => even.
11 = (2, 2, 2, 2, 2, 1), 5 groups of 2 elements with remainder => odd
0 = (?, ?), no groups of 2 elements to consider 0 even, no remainder to consider 0 odd => 0 parity is neutral.
You can insist on that for your own purposes, if you want. But you won’t be able to communicate accurately with the mathematical world, which understands that a remainder of zero, even in this special case, defines evenness; and your alternative version of mathematics would be harder to work with, as we’ve fully explained. The sum of two even numbers is not always even in your world; this, among other things, makes your definition mathematically useless.
The rest of us will continue to do what is reasonable and consistent. There is no “neutral parity”. Integers have even or odd parity, non-integers have none, because the term doesn’t apply. Zero is interestingly different, but it is nevertheless a number, and is valid both as a quotient and as a remainder.
In programming we use (n % 2) sometime (n & 1).
It is oversimplified view about 0 parity (odd or even),
and often we say “0 is even by convention”, because convention is an agreement of convenience,
but if to follow logical deductive reasoning, “0 value is neutral, therefore 0 parity is also neutral”,
$$ a \pm 0 = a $$
for i in range(10):
print(i, i % 2, i & 1)
0 0 0
1 1 1
2 0 0
3 1 1
4 0 0
5 1 1
6 0 0
7 1 1
8 0 0
9 1 1
All you’ve done here is to confirm that computer science agrees with mathematics that zero is an even number: Both characterizations of an even number (by remainder, and by units digit in binary) agree that zero is just like all the other even numbers. Have you not wondered why this “convention” is universally accepted? It’s because of the logical reasoning I’ve shown; it is not just arbitrary convention.
Your “logical deductive reasoning” seems to start, once again, at a non-definition, “0 value is neutral”. That word “neutral” is not a formal mathematical term. And your conclusion does not follow logically from that, anyway.
Any further comments from you will be blocked, because you persist in rejecting proper logic. I can’t waste my time on this.
Let me fix that last one for you:
0 = (), 0 groups of 2 elements with no remainder => even.
(We generally would call those “groups of 2 elements” the “quotient”.)
Why would you care what the quotient is? The only thing that matters is the remainder. 0/2 and 2/2 have a remainder of 0, so 0 and 2 are both even. 1/2 and 3/2 have a remainder of 1, so 1 and 3 are both odd. The quotient is not taken into consideration at all. In logic, the quotient is a “don’t care” when determining parity.
You seem to be the only person in the world who defines n to be even if n/2 is an integer _and not equal to 0_. No one else includes that last requirement. Omitting that special case does not create any inconsistencies or other problems in mathematics, so why not just leave it out? (As this article says, “generalization is good; if you can extend a concept without causing harm, do it!”) On the other hand, including that special case would only complicate mathematics without any benefits.
For example, statements like these:
* “(-1)^n = 1 for even n”
* “(even)+(even)=(even)”
* “(even)+(odd)=(odd)”
* “(odd)+(odd)=(even)”
would have to be expanded to include exceptions like this:
* “(-1)^n = 1 for even n or n=0”
* “(even or zero)+(even or zero)=(even or zero)”
* “(even or zero)+(odd)=(odd)”
* “(odd)+(odd)=(even or zero)”
if you excluded zero as an even number.
Can you think of anything that would be simplified by excluding zero as an even number? Or can you think of any problems that are caused by allowing zero to be even? I don’t want to hear about wings on a pig or legs on a snake or heads on a mannequin or whatever other non-mathematical nonsense you’ve used elsewhere for determining if zero is even.
And if you want to have a special case in your own definition of parity, what is your reason for picking on zero? What makes zero so special to you? Why not pick on a number like 42? It’s just as special as zero. After all, no other number equals 42, and it’s the answer to life, the universe, and everything! You could, for example, define n as even if n/2 is an integer _and is not equal to 21_. That would make just as much sense. The number 42 is way overused anyway. 😉
You appear to be a programmer. You (should) know that special cases are Bad(TM). They increase the number of lines of code and the number of possible code paths (each condition doubles the number of code paths); both increase the likelihood of bugs (which are generally considered bad). A good programmer tries to generalize their code and minimize special cases. Simpler and shorter code with fewer limitations is generally considered to be better than more complicated and longer code with more limitations. The same applies to mathematics.
I’ll end with a quote by one Mr. Albert Einstein: “Everything should be made as simple as possible, but not simpler.”