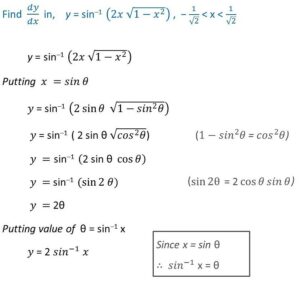(A new question of the week)
It is not uncommon for students to ask about why they get different answers using different methods. Usually the answer is that the answers are really equivalent. This time, the answers really are different! This was partly the result of being taught an incomplete technique, omitting important cautions. And although the question is about calculus, the real issues all involve some tricky trigonometry.
One function, two derivatives?
Here is the question, from Shreshth, at the end of November:
I have to find the derivative of y = arcsin(2x * sqrt(1 – x^2)) .
I can take
x = sin θ or x = cos θ
which will lead me to the answers
2/sqrt(1 – x^2) and -2/sqrt(1 – x^2)
But these derivatives are not equal. Is this possible?
I have attached images for the procedure to solve using x = sin θ:
Thanks.
Shreshth
This is not the usual method for differentiating, which would not involve such a substitution; rather, the substitution is meant to simplify the work of differentiation. The answer obtained is correct; Shreshth didn’t show his own work that gives the wrong answer. Let’s do what I presume he did:
$$\begin{align*}y&=\sin^{-1}(2x\sqrt{1-x^2})\\ \text{ Putting }&x=\cos\theta\\ y&=\sin^{-1}(2\cos\theta\sqrt{1-\cos^2\theta})\\ y&=\sin^{-1}(2\cos\theta\sqrt{\sin^2\theta})\\ y&=\sin^{-1}(2\cos\theta\sin\theta)\\ y&=\sin^{-1}(\sin2\theta) = 2\theta\\ \text{ Putting }&\theta=\cos^{-1}x\\ y&= 2\cos^{-1}x\\ \frac{dy}{dx} &= -\frac{2}{\sqrt{1-x^2}}\end{align*}$$
This does indeed give the wrong sign. Can you see why?
The substitution is unnecessary, and not quite right
Doctor Fenton first answered the explicit question:
A function cannot have two different derivatives. It is possible to be able to compute the derivative in two different ways, yielding two different formulas, but the two formulas must be equivalent. For example, if we differentiate y=sin(2x) by the Chain Rule and obtain
dy/dx = 2 cos(2x) ,
and also write sin(2x) as 2 sin(x) cos(x) and differentiate using the Product Rule to get
dy/dx = 2 cos2(x) – 2 sin2(x) ,
then although the two results look different, they are actually the same, by the identity
cos(2x) = cos2(x) – sin2(x).
This is what we usually find when someone asks about getting two different answers. But the two answers Shreshth got can’t be the same. So what is happening? We’ll get to that later; but first, why is he using this method?
First of all, I don’t know why you are using a substitution to compute the derivative. The computation is straightforward, using the Chain Rule. You write u = 2x√(1 – x2) and use the Chain Rule to write
dy/dx = dy/du * du/dx .
There is no reason to substitute a different formula for x.
The substitution seems to be used to verify an identity that
sin-1(2x√(1-x2) ) = 2 sin-1(x) for -1/√2 < x < 1/√2 ,
so that on this interval, the derivative is just 2/√(1-x2) .
We’ll see the full work without substitution soon. And we’ll also be seeing that this identity is correct … on the given domain. But both substitutions are missing something essential:
Your two substitutions are not equivalent. Writing x = sin(θ) when -1/√2 < x < 1/√2 assumes that θ is in the fourth or first quadrant, so -π/4 < θ < π/4. In this interval for x, we can write x as sin(θ) for θ in the given θ-interval.
Why only in this interval? We’ll see more later, but ultimately it will be because of how we define the inverse function, whose range is taken to be \([-\frac{\pi}{2},\frac{\pi}{2}]\).In the following picture of the unit circle (where the y coordinate of a point is the sine), the red vertical line represents the domain of the inverse sine, the red semicircle represents its range; the blue line and sector represent the stated domain of x, and the implied domain of θ, respectively
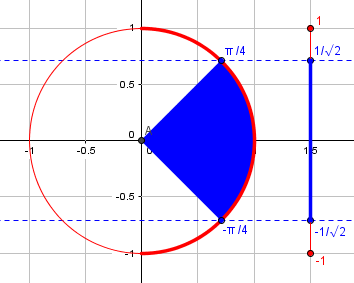
Observe that on this interval, the cosine is positive; this will be important to know later. The important point for the moment is that there are other angles with sines in the given interval, so that the substitution as stated did not uniquely define theta.
But writing x = cos(θ) when -1/√2 < x < 1/√2 assumes that θ is in the first or second quadrant, so π/4 < θ < 3π/4, and the substitutions are not equivalent. When you replace √(1 – sin2(θ)) with cos(θ), that is incorrect in the second quadrant. You need to take the negative square root in the second quadrant. The substitution of cos(θ) for in the given interval for x is not valid.
(I think Doctor Fenton is talking about the (valid) work that was shown, using the sine, not about the (invalid) work, using the cosine, where we actually replace \(\sqrt{1-\cos^2\theta}\) with \(\sin\theta\), which turns out to be valid. I only came to realize this while editing this post.)
Here are the domain and range of the inverse cosine (in red), and the implied domain of θ (in blue):
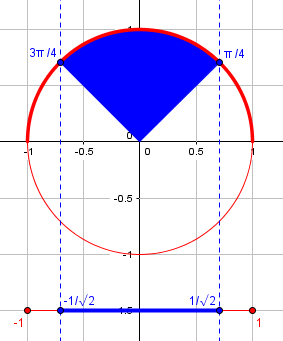
In the second quadrant, the cosine is negative, but the sine is positive. That’s why the radical is, perhaps accidentally, handled correctly. What’s most important, as we’ll see, is that these angles are not in the range of the inverse sine (which is the function explicitly used in the problem).
Doing it directly
Doctor Fenton’s main point is that those complexities are unnecessary:
But mainly, there is no reason to make such a substitution to compute the derivative in this case. The result of using the Chain Rule as I described does lead to a somewhat complicated formula, but this does simplify to 2/√(1-x2), since
2/√(1 – u2) = 2/√(1 – (2x√(1 – x2))2)
= 2/√(1 – (4x2(1 – x2)) = 2/√(1 – 4x2 + 4x4) = 1/(1 – 2x2) ,
since in the given interval for x, you need to write √(1 – 4x2 + 4x4) = (1 – 2x2) to take the positive square root.
Let’s carry out the whole work of differentiating \(\arcsin\left(2x\sqrt{1-x^2}\right)\). We’ll use the fact that \(\frac{d}{dx}\arcsin(u)=\frac{1}{\sqrt{1-u^2}}\frac{du}{dx}\) (by the chain rule), together with the product rule:
$$\frac{d}{dx}\arcsin\left(2x\sqrt{1-x^2}\right)\\=\frac{1}{\sqrt{1-\left(2x\sqrt{1-x^2}\right)^2}}\frac{d}{dx}\left(2x\sqrt{1-x^2}\right)\\=\frac{1}{\sqrt{1-4x^2\left(1-x^2\right)}}\left(\frac{d}{dx}(2x)\cdot\sqrt{1-x^2}+2x\cdot\frac{d}{dx}\sqrt{1-x^2}\right)\\=\frac{1}{\sqrt{1-4x^2+4x^4}}\left(2\sqrt{1-x^2}+2x\frac{-x}{\sqrt{1-x^2}}\right)\\=\frac{1}{\sqrt{1-4x^2+4x^4}}\frac{2(1-x^2)-2x^2}{\sqrt{1-x^2}}\\=\frac{1}{\sqrt{(1-2x^2)^2}}\frac{2-4x^2}{\sqrt{1-x^2}}\\=\frac{1}{1-2x^2}\frac{2(1-2x^2)}{\sqrt{1-x^2}}\\=\frac{2}{\sqrt{1-x^2}}$$
Doctor Fenton’s last comment needs emphasis, as this is where the restricted domain in the problem is used. Near the end of the work, we needed the take the square root of \(1-4x^2+4x^4\). Because we know that \(-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}\), we know that \(0\le x^2<\frac{1}{2}\), so that \(1-2x^2>0\). Outside of the specified interval, we would need the negative sign to get the positive root, and the answer would be … what Shreshth got using the cosine!
Avoiding errors in the substitution
Shreshth replied,
The reason I am using substitutions is because the school books are teaching those. So, I had to use those.
Thanks a lot for your help!
In light of this, Doctor Rick joined in, to correct specific errors in the method being taught:
Hi, Shreshth. I would like to add some comments.
If you are indeed being taught to use substitutions in finding derivatives, then you will need to learn to avoid errors to which that method is prone. Could you tell us more about this substitution method? Under what conditions are you taught to make a substitution, and how do you decide what substitution to make? Could you show another example of this?
We’ll be seeing more examples, but not the general rules that are taught.
In the work you show, with the substitution x = sin θ, there are two errors.
The first error is that no interval is specified for θ, and therefore the substitution is not well defined. For instance, if x = 1/2, we could have θ = π/6 or 5π/6 (or any angle coterminal to these). Saying θ = sin-1 x would have eliminated the ambiguity, because the restriction is built into the definition of sin-1, but we need to be aware of this, and take it into account in the work that follows.
When we make a substitution, we need to fully specify which values of each variable correspond to one another; the substitution must be one-to-one. Just saying “\(x=\sin\theta\)” doesn’t indicate which value of θ corresponds to any given value of x.
That is, though the problem specifies a domain for x, the work (presumably written by the teacher) never specifies a corresponding domain for θ, which sets us up for an error. If the inverse sine had been mentioned in the description of the substitution, rather than only being introduced later, this fault would technically not be present, but it would still be easy to forget the implications that follow.
The next error in the work shown is in replacing √(cos2 θ) by cos θ. Unless we know that cos θ ≥ 0, we need to replace √(cos2 θ) by |cos θ| instead.
In fact (we’re currently looking at the provided work using the sine), for the appropriate values of θ, the cosine is in fact positive, so this step is valid. But it is necessary to pay attention to this; work that blithely takes the root without considering its sign is essentially wrong work, even if the result happens to be correct!
How about the alternative work, using the cosine? That, too is valid at this point. The sine is always positive in the interval of interest. But in other similar examples, there might be trouble.
These two errors together cause the situation that confused you. Doctor Fenton has already pointed these things out to you; I am just re-expressing them in terms of how to avoid errors in a substitution like this.
Actually, the real error in the work is a detail that hasn’t yet been touched upon! The key step in both solutions is $$y=\sin^{-1}(\sin2\theta) = 2\theta$$ But this is not always true. I discussed this in
Mixing Trig and Inverse Trig Functions
There I called this the “second Grant’s Tomb twist”: We are asking, “The sine of what angle is the sine of 2 theta?” But there are many such angles; what we are really asking, without realizing it, is, “The sine of what angle, between \(-\frac{\pi}{2}\) and \(\frac{\pi}{2}\), is the same as the sine of 2θ?”
In the sine-substitution method, since we are told that \(-\frac{\pi}{4}<\theta<\frac{\pi}{4}\), we know that \(-\frac{\pi}{2}<2\theta<\frac{\pi}{2}\), which is in the range of the inverse sine, so it is true that \(\sin^{-1}(\sin2\theta) = 2\theta\). (Were you wondering why they choose that odd domain for x? This is why!)
But in the cosine-substitution method, we have to specify instead that \(\frac{\pi}{4}<\theta<\frac{3\pi}{4}\), and can conclude that \(\frac{\pi}{2}<2\theta<\frac{3\pi}{2}\), which covers the second and third quadrant. There, the inverse sine is not the same angle, but rather an angle in the first or fourth quadrant. This will be revealed in the graph we are about to see.
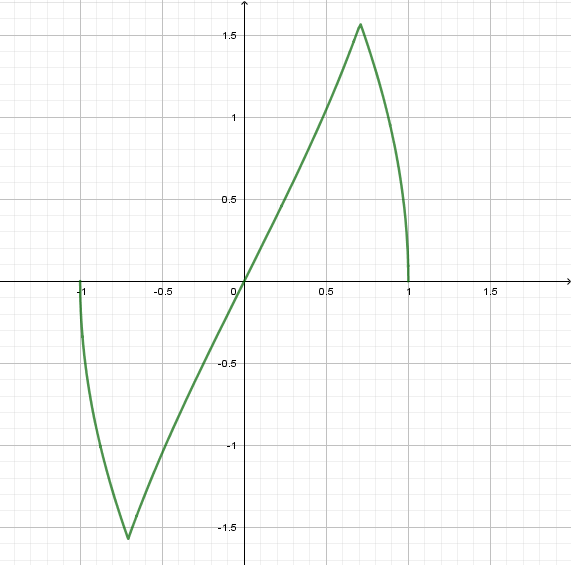
The fact that the work shown makes no reference to the domain of x, while the problem did so, should raise a warning in your mind. You ignored this domain restriction in your initial statement of the problem, but it turns out to be critical! When we graph the function you are differentiating, we discover that something important happens at the endpoints of the given domain:
Notice the sharp change in slope (derivative) at x = ±1/√2 ≈ ±0.707. If you complete the differentiation using the standard (chain rule) method that Doctor Fenton discussed, you will find that
{ 2/√(1–x2), |x| ≤ 1/√2 dy/dx = { { -2/√(1-x2), 1/√2 < |x| ≤ 1which shows that your two derivatives are both correct, but for different intervals of the full domain, [–1, 1].
This is what I pointed out above, when I carried out the work just for the specified interval, but mentioned the sign change needed outside that interval.
What causes those sharp bends? Here is the same graph, of \(y=\sin^{-1}(2x\sqrt{1-x^2})\) (green), compared with the supposedly equivalent function, \(y= 2\sin^{-1}x\) (red dots), and Shreshth’s version, \(y= 2\cos^{-1}x\) (purple dots):
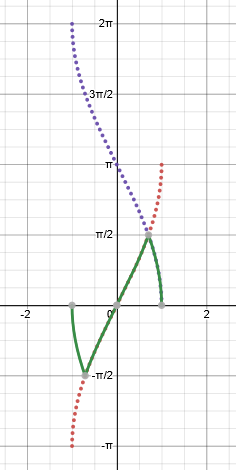
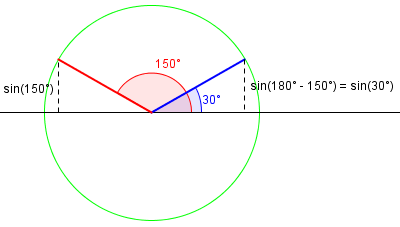
The inverse sine is restricted to \([-\frac{\pi}{2},\frac{\pi}{2}]\), so it “folds” either of the other two graphs back toward zero when they exceed the bounds. For instance, for \(\frac{\pi}{2}<\theta<\pi\), in quadrant II, \(\sin^{-1}(\sin\theta) = \pi-\theta\), as shown here, in an example using degrees:
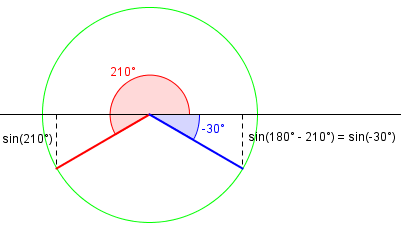
And for \(\pi<\theta<\frac{3\pi}{2}\), in quadrant III, it is still true that \(\sin^{-1}(\sin\theta) = \pi-\theta\), as shown here:
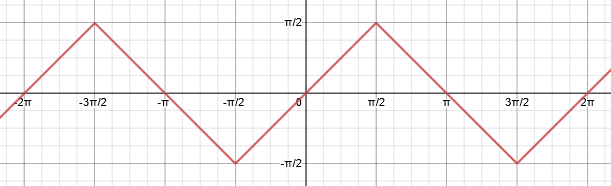
As a result, here is the actual graph of \(y=\sin^{-1}(\sin\theta)\):
Another example of the method, and its flaws
Shreshth sent several examples from his teacher, of which I’ll show only the first for now (and another later):
I have attached a few more examples given by my teacher:
It is entirely possible that the NCERT books (the books we use in India) did not mean for us to use the substitution method. But teachers here focus more on the easiest ways out with maximum marks, and over the years I have found that for the evaluators the solutions I attached are enough however wrong the solutions are.
So, I will just be using the chain rule from now on.
This particular example has a typo (an extra 2 in the denominator); my impression is that the problem is intended to be what was written below “Putting x = tan θ“.
Doctor Rick replied:
You did not answer my questions about the situations in which you are taught to use the substitutions, and how you are to decide which substitution to use. Your examples, however, suggest that this technique is taught specifically for functions that are inverse trig functions of certain classes of function, perhaps with a specific substitution to use for each class.
I myself prefer to minimize how many specific formulas I memorize. It would appear that they have a long list.
As Doctor Fenton suggested, this technique amounts to simplifying the function before differentiating, so that you only need to differentiate inverse trig functions of x. I would assume that you still sometimes encounter problems in which you can’t simplify that much, so that you need to use the Chain Rule.
This is one of the dangers of focusing on memorized formulas: Not every problem will be amenable to such a formula.
As your initial problem shows, the simplification has some tricky points that are easy to miss. Also, my guess is that you need to remember a number of rules, and they will not always apply. In the long term, the Chain Rule is one rule that will always work, so it is the most worth knowing. However, I recognize that schools everywhere probably “teach to the test”, and if the test is expected to have a lot of problems like these, I can understand specific methods being taught to solve them faster.
We do seem to see this sort of teaching particularly in South Asia, judging by the questions we get; but it can happen anywhere.
Your first example here, differentiating y = sin-1(2x/(1+2x2), is incorrect! After the substitution x = tan θ, the function was miscopied, so the wrong function was differentiated. When I differentiate the original function (using the Chain Rule), the result is not as simple as all your other examples. On the other hand, when I differentiate y = sin-1(2x/(1+x2) carefully, I find that it ought to have a domain restriction like the others (the derivative is different on |x| ≤ 1 than on |x|> 1).
So, even correcting the 2 in the denominator, the problem this time is stated incorrectly, by not specifying the domain. The solution implicitly assumes that \(\theta=\tan^{-1}x\) and therefore is in the interval \(-\frac{\pi}{2}<\theta<\frac{\pi}{2}\). But, as in the original problem, in order for it to be true that \(\sin^{-1}(\sin2\theta) = 2\theta\), we need to restrict further to \(-\frac{\pi}{4}<\theta<\frac{\pi}{4}\), corresponding to \(-1<x<1\).
Here is a graph of \(\displaystyle y=\sin^{-1}\left(\frac{2x}{1+x^2}\right)\), again with the given function in green, the claimed equivalent (valid only between -1 and 1), \(y=2\tan^{-1}x\), in red dots, and the equivalent for x > 1, \(y=2\cot^{-1}x\), in purple dots:
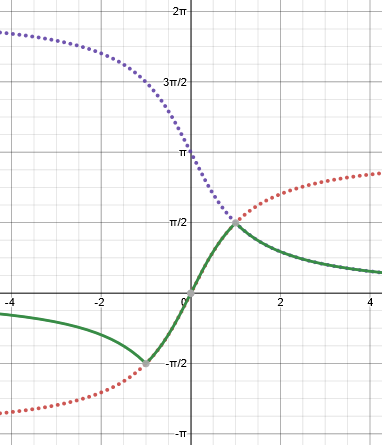
The correct “simplified” form of the function is $$\left\{\begin{matrix}2\cot^{-1}(x)-2\pi & \text{if }x<-1\\2\tan^{-1}(x) & \text{if }-1\le x\le 1\\2\cot^{-1}(x) & \text{if }x>1\end{matrix}\right.$$ And the derivative is negative outside of the interval \([-1,1]\).
One more example
Shreshth included four other examples, but I’ll just look at the last one he sent, which is a little different:

Here you are evidently expected to recognize the triple-angle tangent formula, which I don’t know on sight. An issue similar to the others arises here, but this time the graph is not continuous:
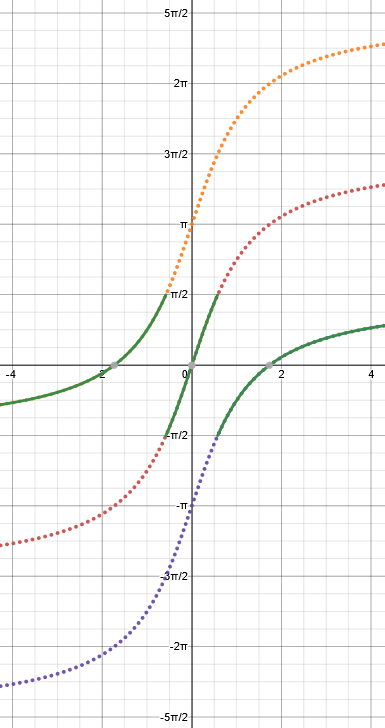
You may notice that the given function is undefined at the endpoints of the given domain, so I would add four open circles if I drew the graph by hand.
The correct “simplification” this time requires shifting the inverse tangent graph up on the left, and down on the right. We could write it as $$\left\{\begin{matrix}3\tan^{-1}(x)+\pi & \text{if }x<-\frac{1}{\sqrt{3}}\\3\tan^{-1}(x) & \text{if }-\frac{1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}}\\3\tan^{-1}(x)-\pi & \text{if }x>\frac{1}{\sqrt{3}}\end{matrix}\right.$$
Again, the answers to all the questions as provided by the teacher are correct where a domain was specified, but the lack of any explanation of the circumstances that make them correct can lead students astray when the problem requires more care. Always be careful when you take an inverse function of a function that is not one-to-one! This applies to the “Grant’s Tomb problem”, and also to the square root of a square or a Pythagorean identity.