(A new question of the week)
Last week I discussed several Ask Dr. Math questions about factoring quartic polynomials, which had been on my list of potential topics. That list also included a question on that topic from three years ago, that didn’t make it into the blog at the time. That will lead us into a 133-year-old algebra book, which explores the topic a little more deeply than modern books generally do. As a bonus, we’ll get many exercises for you to try!
How do I choose the right tool?
The question is from John, on the first day of 2019:
I am very bad at factoring polynomials. For example,
x2 – 2x(a + b) – ab(a – 2)(b + 2) … [A]
I tried to find its factors by +/- (a + b)2 because a chapter on factoring in my book suggests I do that. Unfortunately this approach doesn’t lead anywhere and I am out of ideas.
Another example is
x3 (a + 1) – xy(x – y)(a – b) + y3 (b + 1) … [B]
I have no idea what to do here; I tried to open every expression and check if I can apply grouping since that’s what my book tells me to do.
That’s my biggest problem regarding factoring. I don’t know how to approach problems like that. My book has a list of strategies which can be used but most of the time none of them work. So my question is how to think about these problems? I know long division and I understand the distributive property. I tried to guess possible factors then use long division to check if they give a satisfying answer but that seems very inefficient and time consuming. I tried to multiply different expressions and see what I get, but again this approach involves guessing. So can anybody explain factoring to me?
I’ve added the labels [A] and [B] so we can refer back to these problems later.
The initial attempt at [A] is presumably based on the “wishful thinking” approach we saw last time: We see that the polynomial looks like the beginning of \(x^2-2x(a+b)+(a+b)^2 = (x-(a+b))^2\), so we add and subtract that third term to see what happens, hoping perhaps that we will get a difference of squares. We don’t: $$x^2-2x(a+b)+ab(a-2)(b+2)\\ = x^2-2x(a+b){\color{Red}{+(a+b)^2-(a+b)^2}}+ab(a-2)(b+2)\\ = (x-(a+b))^2-(a+b)^2+ab(a-2)(b+2)$$ and the final terms don’t seem useful. There’s nothing wrong with that; factoring is the sort of endeavor where you may find yourself with the entire contents of your toolbox scattered on the workbench while you try one last thing. Then it may work … or it may not! As we pursue these problems and more, we’ll be buying ourselves a few new tools, and finding new uses for old ones.
Factoring [A] as a trinomial
I answered:
Hi, John.
I can factor the first by the usual method for quadratics: Look for a pair of “numbers” whose sum is -2(a + b) and whose product is -ab(a – 2)(b + 2). One of the natural choices works.
I have to admit that, looking at [A] just now, three years later, I didn’t think of that! Just as we would factor \(x^2-7x+12\) by looking for a pair of numbers whose product is 12 and whose sum is -7 (obviously -3 and -4), and concluding that the factors are \((x-3)(x-4)\), we can try various combinations of factors. Taking the product as \(\left[-ab\right]\cdot\left[(a-2)(b+2)\right]\) the sum will be $$\left[-ab\right]+\left[(a-2)(b+2)\right]=2a-2b-4$$ which is wrong.
If we tried \(\left[a(a-2)\right]\cdot\left[-b(b+2)\right]\), resulting in the sum $$\left[a(a-2)\right]+\left[-b(b+2)\right]=a^2-2a-b^2-2b$$ it would have the wrong degree, since we want the sum to be linear in a and b.
But what about taking the product as \(\left[-a(b+2)\right]\cdot\left[b(a-2)\right]\)? This gives the sum $$\left[-a(b+2)\right]+\left[b(a-2)\right]=-ab-2a+ab-2b=-2(a+b)$$
We’ve got it! The factorization is $$x^2-2x(a+b)+ab(a-2)(b+2)=(x-a(b+2))(x+b(a-2))\\ =(x-2a-ab)(x-2b+ab)$$
At this point, however, I had no idea how to handle [B].
I would like to see the actual list of strategies you were taught (word for word), and exactly what they say as hints for these two problems. Presumably you are learning advanced techniques beyond the usual, at least in part, since we don’t usually have so many variables in a factoring problem.
What course is this, and what is the textbook?
Not the usual modern textbook!
John replied,
Hi Mr Peterson thank you for your response I am reading a book called A Treatise on Algebra by Charles Smith. I am taking pre calculus college course. I wanted to check some more challenging problems since the ones provided in class were too easy. My instructor is reluctant to advise on topics not related to the coursework provided by him because of the time constraints so I decided to ask here.
Factoring techniques presented by Smith are these:
- Factor out monomials.
- Check for expressions like an – bn and other known identities.
- x2 + (a + b)x + ab = (x + a)(x + b) (now I see that it can be applied in the first problem above).
- Solve the quadratic then use its roots.
- Complete the square.
- Rearrange and group the terms.
There are examples provided in the book but they are very simple like -ax3 – x2 + ax + 1 … [C]; I have no problems solving these. However I seem to get easily confused when the number of variables tends to increase like in the problems like this one
x4 – 2x2 a2 – 2x2 b2 + a4 + b4 – 2a2 b2 … [D]
Problems like multiplication and division have clear algorithms which I can follow; is there an algorithm for factoring?
The name of the book sounds old-fashioned, so John appears to have found a book from another generation, which may well cover material we no longer teach! And it is understandable that a teacher would consider this outside of his duties; this is our job!
Factoring [C] by grouping
Problem [C] is indeed a typical example of factoring by grouping: $$-ax^3-x^2+ax+1 = -x^2(ax+1)+1(ax+1)\\ =(1-x^2)(ax+1) =(1+x)(1-x)(ax+1)$$ I would usually factor out -1 first to avoid negative leading coefficients: $$-(ax^3+x^2-ax-1) = -(x^2(ax+1)-1(ax+1)\\ = (x^2-1)(ax+1) = (x+1)(x-1)(ax+1)$$ The important thing is that this only works for special cubics, and can’t be expected to work in general. That’s how factoring works.
Factoring [D] as a trinomial … and more!
Let’s try [D]. If we rewrite it as a polynomial in x, we get $$x^4-2(a^2+b^2)x^2+(a^4-2a^2b^2+b^4)$$ We can try to factor it, again as an ordinary quadratic trinomial: $$x^4-2(a^2+b^2)x^2+(a^4-2a^2b^2+b^4) = x^4-2(a^2+b^2)x^2+(a^2-b^2)^2$$ This is so close to the perfect square $$x^4-2(a^2+b^2)x^2+(a^2+b^2)^2 = (x^2-(a^2+b^2))^2$$ that I wonder if it could be a typo … but what if we try that “wishful thinking” idea again! Let’s add and subtract \(4a^2b^2\) to “make it so”:
$$x^4-2(a^2+b^2)x^2+(a^4-2a^2b^2+b^4)+4a^2b^2-4a^2b^2\\ = [x^4-2(a^2+b^2)x^2+(a^4+2a^2b^2+b^4)]-4a^2b^2\\ = (x^2-(a^2+b^2))^2-(2ab)^2\\ = [(x^2-(a^2+b^2))-(2ab)][(x^2-(a^2+b^2))+(2ab)]\\ = (x^2-(a^2+2ab+b^2))(x^2-(a^2-2ab+b^2))\\ = (x^2-(a+b)^2)(x^2-(a-b)^2)\\ = (x-(a+b))(x+(a+b))(x-(a-b))(x+(a-b))\\ = (x-a-b)(x+a+b)(x-a+b)(x+a-b)$$
We did it! And we just had to use several “basic” methods (notably the difference of squares) over and over, never giving up.
But I hadn’t solved this yet when I responded.
Factoring is an art
I was intrigued by the book, which on one hand sounds unexpectedly modern in its list of methods, but not in its selection of problems:
Thanks.
The techniques you listed are only the usual methods, not anything advanced – the list is entirely ordinary.
These examples, on the other hand, are extraordinary! I rarely, if ever, see factoring problems with parameters like a and b. As you found, the first yields to an ordinary method; I’m not convinced that the second does.
There is no mere algorithm for factoring; it is very much an art that requires skill. See the following pages for examples of more advanced techniques, as well as comments about the difficulty of factoring in general:
Factoring a Multivariate Polynomial: Strategies Beyond Grouping
Advanced Polynomial Factoring Methods
Factoring Quartic Expressions with No Real Zeros
Don’t try to read through all of those; I don’t know everything mentioned there myself! But notice that even these don’t include parameters.
Those links are to pages I looked at last week but considered too advanced to include in the blog; maybe we’ll look at them some other time. (To read them where they are, you’ll need to set up a free account.)
Factoring [B] by guessing the form
I used an idea from the first of those pages to work out [B]:
I found that I can use one of the methods mentioned to work out your second example. What I did was to observe that the polynomial is homogeneous in x and y (that is, the total degree of each term is the same, thinking of a and b as mere numbers), so that, being 3rd degree, it should factor as something like
(mx2 + nxy + py2)(qx + ry)
where each factor is homogeneous.
I expanded this, then matched up coefficients with the coefficients of your polynomial (after expanding it in x and y, keeping a and b in their parentheses); for instance, mn = (a + 1). Then, thinking of each factor like (a + 1) or (a – b) as a prime number, I looked for a solution to the system of four equations in m, n, p, q, r. This involved some trial and error, but not too much. Try that.
This technique of choosing a likely form for the factors and matching coefficients is one we saw last week. Let’s carry it out: $$(mx^2+nxy+py^2)(qx+ry) = mqx^2+(mr+nq)x^2y+(nr+pq)xy^2+pry^3$$ and $$x^3(a+1)-xy(x-y)(a-b)+y^3(b+1)=(a+1)x^3+(b-a)x^2y+(a-b)xy^2+(b+1)y^3$$
so equating coefficients gives the system $$\left\{\begin{matrix}mq=a+1\\ mr+nq=b-a\\ nr+pq=a-b\\ pr=b+1\end{matrix}\right.$$
The first equation implies that either \(m=1\) and \(q=a+1\), or \(m=a+1\) and \(q=1\); likewise, the last equation implies that either \(p=1\) and \(r=b+1\), or \(p=b+1\) and \(r=1\). This gives four possible combinations we can check out:
If \(m=1,\ q=a+1,\ p=1,\ r=b+1\),
then \((b+1)+n(a+1)=b-a\) and \(n(b+1)+(a+1)=a-b\),
both of which imply \(n=-1\).
If \(m=1,\ q=a+1,\ p=b+1,\ r=1\),
then \(1+n(a+1)=b-a\) and \(n+(a+1)(b+1)=a-b\),
so that \(\displaystyle n=-ab-2b-1\) and \(\displaystyle n=-\frac{a-b}{(a+1)(b+1)}\) which is inconsistent.
If \(m=a+1,\ q=1,\ p=1,\ r=b+1\),
then \((a+1)(b+1)+n=b-a\) and \(n(b+1)+1=a-b\),
so that \(\displaystyle n=-ab-2a-1\) and \(\displaystyle n=\frac{a-b-1}{b+1}\) which is inconsistent.
If \(m=a+1,\ q=1,\ p=b+1,\ r=1\),
then \((a+1)+n=b-a\) and \(n+(b+1)=a-b\),
so that \(n=b-2a-1\) and \(n=a-2b-1\) which is inconsistent.
(Once I found the first, I didn’t really need to try the others, since all I need is one set of coefficients.)
So our coefficients are $$m=1\\ n=-1\\ p=1\\ q=a+1\\ r=b+1$$ and we have the factorization $$x^3(a+1)-xy(x-y)(a-b)+y^3(b+1)=(x^2-xy+y^2)((a+1)x+(b+1)y)$$ which checks out when multiplied.
But we have to wonder whether the original partially factored form could have been of use. We’ll see another way shortly.
Looking at the book
I don’t think you need to be anxious about being able to do these problems; but if you can, you will be far ahead of your class!
Now, having written all that, I looked for your book online, recognizing that the title looked old. Old books often are more challenging than modern ones.
Are you referring to this book, from 1888?
A Treatise on Algebra, By Charles Smith
I see your problems on pages 64-65. I haven’t looked carefully through its examples to see if there is a good parallel to this one; I’ll have to spend some time looking.
Here are the problems, which you may find interesting; our [A], [B], and [D] are #20, 32, and 36:
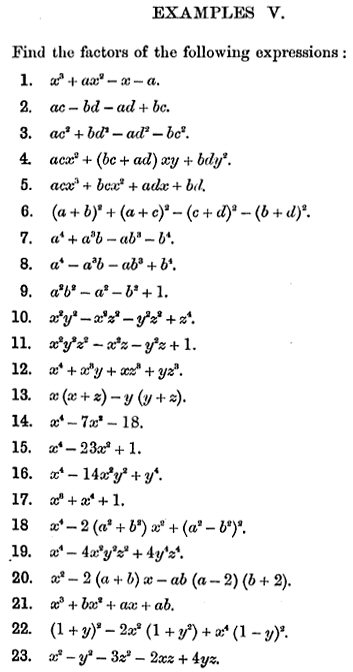
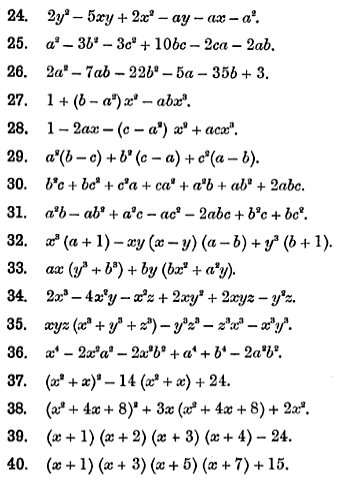
Here is part of what is taught before these problems, including our [C] as the first example:
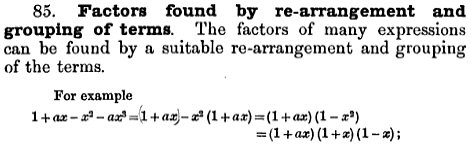
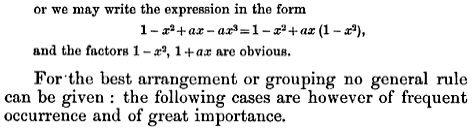
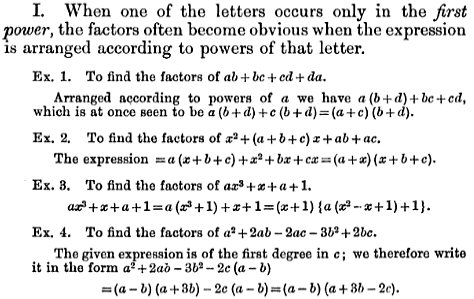
When I teach the basic form of “factoring by grouping”, I generally recommend ordering terms in descending order by the powers of x; but examples 2 and 3 here are given to us already written that way, and choosing to order instead by the degree of a parameter instead hadn’t occurred to me.
Factoring [B] an easier way
After reading that, I had more to say:
Hi again!
I just read page 61 (section 85, about grouping), and decided to follow the suggestion of focusing on a, which occurs only in the first power. It worked like magic.
Collect the terms containing a; then notice that many of the remaining terms contain b, so collect those; and then collect the other two terms.
Now factor the GCF from each of these three groups of terms, and everything will fall into place (if you also notice a sum of cubes).
In other words, the technique being taught here is to look for the easiest thing to do, and hope that will work!
Here’s the work on [B] for this method:
$$x^3(a+1)-xy(x-y)(a-b)+y^3(b+1)\\ =a(x^3-xy(x-y))+b(xy(x-y)+y^3)+x^3+y^3\\ = ax(x^2-xy+y^2)+by(x^2-xy+y^2)+(x+y)(x^2-xy+y^2)\\ = (ax+by+x+y)(x^2+xy+y^2)\\ = ((a+1)x+(b+1)y)(x^2+xy+y^2)$$ as before, with considerably less work.
John wrote back:
Hi thanks for all the help. Thanks to you I managed to solve most the exercises. It seems so simple now almost embarrassing I did not notice those tricks immediately. 😀
Nor did I.
I responded:
Most tricks seem simple once you see them.
This was fun.
As I often tell students, my definition of “fun” is “challenging”.
Symmetric polynomials
Then he had another question:
Hi can you help me with one more factoring problem?
(y – z)5 + (z – x)5 + (x – y)5 … [E]
I know that it has three factors (x-y)(z-x)(y-z) because if I replace x by y or z by x or y by z I get zero. However the degree is 5 so there has to be either two more factors or one factor of the second degree. I know this because there’s an example of a 5th degree polynomial in the book we talked about above and the author demonstrates how to factor it. Here is the example:
b2c2(b – c) + c2a2(c – a) + a2b2(a – b) … [F]
It factors into
-(b – c)(c – a)(a – b)(bc + ca + ab)
To begin with how does he know that the fourth factor will be of second degree and not two factors of the 1st degree? Secondly, how did he come up with this expression; was it just a guess? I know that the polynomials in the example and in my problem are symmetric and that symmetric polynomials are constructed from the simpler symmetric polynomials, so is there like a list of simple polynomials you can look at to help you guess the factor?
In answer to his last question here, which I never explicitly answered, what he wants are called elementary symmetric polynomials, which you can also read about here.
I responded:
I see the problem on page 73, and read the previous pages. The techniques there are similar to some in the pages on our site that I referred to earlier. It is interesting reading!
I imagine that if there were two linear factors, you could still find them by assuming a second-degree factor and discovering that it could be factored further, so it is not necessary to know which is the case.
Here are the problems on page 73, where [E] is exercise 2:

Here is part of what is taught leading up to these, on page 71:

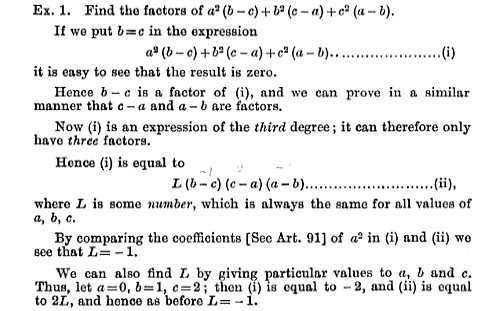
And here is the work for example [F]:
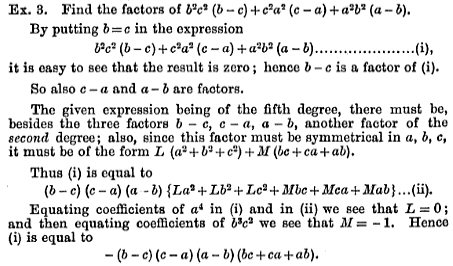
In both of these examples, there is an element of guessing: He tries setting two variables equal to see if \(b-c\) might happen to be a factor. So in these problems, which are contrived to use the ideas he is teaching, we can expect such things to work!
I continued, correcting a slightly wrong implication there:
He explains the reasoning for this guess, namely that the factors can be expected to have the same symmetry as the original (though there is no guarantee, as explained in the last response in Factoring a Multivariate Polynomial: Strategies Beyond Grouping). Ultimately, yes, it is a hopeful guess, an “ad-hoc technique” in Dr. Vogler’s terms). So he assumes the squared terms all have the same coefficient, as do all the cross-terms like xy. That is required for symmetry.
Smith said that the new factor must be symmetrical; this is true because the other factors (taken together) are. But Doctor Vogler pointed out in that page that, in general, a symmetrical polynomial may have factors that are not, giving an example:
Not all symmetric polynomials factor into symmetric factors. For example, (x + y)(x + z)(y + z) is symmetric in three variables, but none of the factors is. However, a symmetric polynomial that factors into terms of different degrees will have symmetric factors. The reason is that permuting the variables doesn't have to leave all of the factors unchanged, but it does have to leave the collection of factors unchanged, which means that the most it can do is rearrange the factors. (Look at how swapping x and y, for example, will rearrange the factors in my example polynomial.)
Factoring [E] by guessing the form
Our quadratic factor must be symmetric, which means the coefficients of any terms that would be exchanged by permutation of the variables must be the same:
For the problem you are asking about, you can just follow the example, guessing that the factorization has the form
(y-z)(z-x)(x-y)(L(x2 + y2 + z2) + M(yz + zx + xy))
The fifth degree terms must be 0, but you can look at the fourth degree terms to find the coefficients.
So let’s close by finishing the work for [E].
We assume that $$(y-z)^5+(z-x)^5+(x-y)^5\\ = (y-z)(z-x)(x-y)(Lx^2+Ly^2+Lz^2+Myz+Mzx+Mxy)$$
The product of three linear factors expands to $$xy^2+yz^2+x^2z-x^2y-y^2z-xz^2$$
Multiplying this by the quadratic factor, we get $$Lx^3y^2+Lx^2yz^2+Lx^4z-Lx^4y-Lx^2y^2z-Lx^3z^2\\ +Lxy^4+Ly^3z^2+Lx^2y^2z-Lx^2y^3-Ly^4z-Lxy^2z^2\\ +Lxy^2z^2+Lyz^4+Lx^2z^3-Lx^2yz^2-Ly^2z^3-Lxz^4$$ $$+Mxy^3z+My^2z^3+Mx^2yz^2-Mx^2y^2z-My^3z^2-Mxyz^3\\ +Mx^2y^2z+Mxyz^3+Mx^3z^2-Mx^3yz-Mxy^2z^2-Mx^2z^3\\ +Mx^2y^3+Mxy^2z^2+Mx^3yz-Mx^3y^2-Mxy^3z-Mx^2yz^2$$
This simplifies to $$-Lx^4y+Lx^4z+(L-M)x^3y^2+(M-L)x^3z^2\\ +(M-L)x^2y^3+(L-M)x^2z^3+Lxy^4-Lxz^4\\ -Ly^4z+(L-M)y^3z^2+(M-L)y^2z^3+Lyz^4$$
We could now expand the LHS, and equate coefficients. But we don’t really need to do all that to solve for two constants, do we? We only need two equations. As I suggested, we could just pick a couple terms in the expansion.
The term in the LHS with degree 5 in x will be \(-x^5+x^5 = 0\), which is good since the RHS can have no such term.
The terms in the LHS with degree 4 in x are \(5x^4z-5x^4y\); in the RHS we get \(-x^2(y-z)Lx^2=Lx^4z-Lx^4y\), so we know that \(L=5\).
What of the terms with degree 0 in x? For the LHS, we have $$(y-z)^5+z^5-y^5=-5y^4z+10y^3z^2-10y^2z^3+5yz^4+z^5$$ and for the RHS we have $$-yz(y-z)(Ly^2+Lz^2+Myz)=-Ly^4z-(M-L)y^3z^2+(M-L)y^2z^3+Lyz^4$$ Equating coefficients, we see again that \(L=5\), and that \(M-5=-10\) so that \(M = -5\).
So our factorization is $$(y-z)^5+(z-x)^5+(x-y)^5\\ = (y-z)(z-x)(x-y)(5x^2+5y^2+5z^2-5yz-5zx-5xy)\\ = 5(y-z)(z-x)(x-y)(x^2+y^2+z^2-yz-zx-xy)$$
Can the quadratic factor be factored further? I suspect not, for several reasons. But let me know if you find otherwise!

By Symmetry:
(x^2 + y^2 + z^2 – yz – zx -xy) = (x + y + z)^2 – 3(xy+yz+zx)
Not sure if that makes things much better… But there it is!
Mike
I don’t see that this helps factor the expression on my last line; but there’s probably a lot I don’t know about symmetric polynomials.