(A new question of the week)
Since we’ve been doing a little trigonometry this week, let’s look at a recent set of questions from a student in the Philippines, all about compositions of trig and inverse trig functions. This is a topic with some interesting little surprises, and several of us answered, to give a variety of voices.
Trig(inverse trig)
First, a very simple question:
Can we find cos(arccos(3/5)) manually? I’m well aware that there is a rule cos(arccosx) = x. But the 3/5 is bugging me.
I tried to compute it without using a calculator.
So I calculate arccos(3/5) first, which is cos x = 3/5. While finding x, I know that cos = x/radius so, x = 3 and radius = 5 and create a right triangle and tried to find the angle… um… yeah. That’s my problem, I don’t know how to compute for the angle. Or should I use calculator now? (It’ll be boring.)
The problem is much easier than he made it. He is using the definition of the cosine of an angle as the ratio x/r of a point on the terminal ray, but then wants to actually find the angle without the calculator. That isn’t needed, and in fact can’t be done by hand! I took this one:
You already have calculated the answer manually! The “rule” cos(arccos(x)) = x is not just a rule; it is a fact, essentially the definition of arccos, namely that it is the inverse of the cosine. This is how you find that cosine.
I think you may have confused yourself by using “x” with two meanings (the angle and the x-coordinate). Let’s give the angle its own name: You want to find cos(arccos(3/5)), so you want the cosine of an angle θ = arccos(3/5); this tells you that cos(θ) = 3/5. That is the answer!
Finding the answer manually does not mean finding every step of the expression manually; you can’t do that at all! It just means thinking about the expression and using what you know. You are smarter than your calculator!
I didn’t tell the following joke, because you have to be American to get it. I call this type of question the Grant’s Tomb problem, from the riddle, “Who is buried in Grant’s Tomb?” Answer: (President Ulysses S) Grant, of course! (It’s a New York City monument.) Actually, if you follow that link, you’ll see that there’s a twist or two to the joke; I’ll have my own twists later!
But the idea is that \(\cos(\arccos x)\) can be read as, “What is the cosine of the angle whose cosine is x?“, much as “Who is buried in x‘s grave?” is x. The answer is in the question — there’s no thinking to do … unless the input to the inverse trig function is outside its domain, as in \(\cos(\arccos \frac{5}{3})\), which is an undefined expression. This is the first Grant’s Tomb twist: no one is actually buried in the tomb, as the bodies are in raised sarcophagi; and there is no angle whose cosine is 5/3.
Inverse trig(trig)
In this series of questions, we didn’t get to the more twisty one: an inverse function of a trig function. I’ll just mention it briefly here, as this is where the bigger twist comes in.
Suppose we turn the question around, and want \(\arccos (\cos \theta) \). This can be read as, “What is the angle whose cosine is the cosine of θ?“, so you might immediately think the answer is θ. The trouble is that there are actually infinitely many angles with the same cosine; the expression has to be refined using the range of the inverse cosine: “the angle in \([0, \pi]\) whose cosine is the cosine of θ.” For example, \(\arccos(\cos 30°) = 30°\), because 30° is in quadrant I.
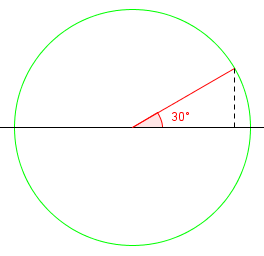
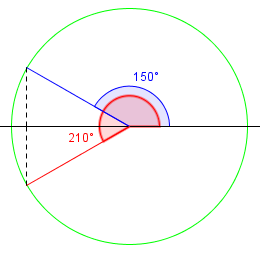
But \(\arccos (\cos 210°) = 150°\), because these two angles (in quadrants II and III) have the same cosine, but the value of an inverse cosine must be in quadrant I or II. We could say this is the second Grant’s Tomb twist: in reality both Grant and his wife are in the same tomb, so there is more than one correct answer, and we have to choose the appropriate one. (If English pronouns were gendered, the choice would depend on the gender of our “who” — its range.)
Trig(other inverse trig)
Now we move on to the next question:
Find csc(arccos(3/5)).
I used a calculator for arccos(3/5), which is unbearably boring and unsatisfactory, and I got 53.13° . Then I have now csc(53.13° ) then used calculator, again (bruh!), which results to having 1.25 as an answer.
So my concern here is the proper “manual” solution.
This time, we want to use the given cosine to find a different function of the same angle. I took this one, too:
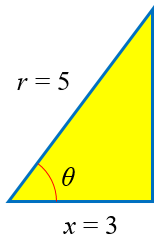
You want csc(arccos(3/5)). That is, you want csc(θ), where cos(θ) = 3/5.
Find the sides of the right triangle for this angle, and find csc(θ) from that.This way of thinking, defining an intermediate variable θ, will be even more useful for the other two questions you asked, which I will not have time for this morning (but someone else may).
Like the first problem, here we can paraphrase the problem as “What is the cosecant of an angle whose cosine is 3/5?” (This one is like “What is the first name of the person buried in Grant’s Tomb?” asking for different information than what is given.) The range of the inverse function can play a small role in questions like this, telling us in this case that we are talking about an angle in quadrant I, not in quadrant II, which can tell us the sign of the answer (though in this case, the sign of the cosecant would be positive in any case). But the main focus is on finding the necessary sides of the right triangle (or coordinates of a point on the terminal ray). A picture is helpful.
He replied,
I used Pythagorean Theorem to find the missing side. Let y be the missing side. So y^2 + 3^2 = 5^2. Then the result is 4. Which is also the opposite side of the triangle. Knowing that sin is opp/hyp (4/5), then csc is hyp/opp which is 5/4.
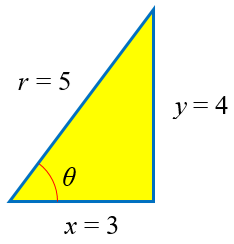
He did well. In other problems like this, the angle would not be in the first quadrant, and there would be some extra considerations of sign, but the same essential method would be used.
I had left a couple other more elaborate questions unanswered, as I was about to leave on a trip. Others took those.
Trig(sum of inverse trigs)
The next question was a step beyond the others:
Find cos(arctan(2) + arctan(3)).
First, I solve for both arctan(2) and arctan(3):
tan x= 2, tan x=3.
I know that tan = y/x so I’ll assume that y = 2 and y = 3, then I create a right triangle then compute for hypotenuse and I got sqrt 5 and sqrt 10, respectively. My problem is how I will know the angle which is also the answer for arctan, right?
Doctor Rick took this, first pointing out the confusing use of variables:
Be careful: don’t use the same variable to mean two different things. You might define:
tan x = 2; tan y = 3
Now, using ideas from other problems you have asked about lately, you can find sin x, cos x, sin y, and cos y (knowing that x and y are in quadrant 1 since they are arctangents of positive numbers).
To finish, you know a formula for the cosine of a sum of two angles, I’m sure.
Here the problem can be paraphrased as, “What is the cosine of the sum of two angles whose tangents are 2 and 3, respectively?“; Doctor Rick used x and y to represent the two angles. Then we just have to use the angle-sum formula to find the required cosine.
I will use A and B for the two angles, so I can use x and y as needed in describing coordinates or sides of triangles. So the question becomes, “What is the cosine of the sum of angle A (whose tangent is 2) and angle B (whose tangent is 3)?” Here is the detailed work:
Since tan(A) = 2, we can make a right triangle with opposite side \(y=2\) and adjacent side \(x=1\); the hypotenuse is
\(r=\sqrt{5}\). So \(\sin(A) = \frac{2}{\sqrt{5}}\), and \(\cos(A) = \frac{1}{\sqrt{5}}\).
Similarly, tan(B) = 3, we can make a right triangle with opposite side \(y=3\) and adjacent side \(x=1\); the hypotenuse is
\(r=\sqrt{10}\). So \(\sin(B) = \frac{3}{\sqrt{10}}\), and \(\cos(B) = \frac{1}{\sqrt{10}}\).
Now we can put these values into the angle-sum formula:
\(\cos(A+B) = \cos(A)\cos(B) – \sin(A)\sin(B) = \frac{1}{\sqrt{5}} \frac{1}{\sqrt{10}} – \frac{2}{\sqrt{5}} \frac{3}{\sqrt{10}} = \frac{-5}{\sqrt{50}} = -\frac{1}{\sqrt{2}} \).
To check, what do we get using the calculator? \(\arctan(2) = 63.43°\); \(\arctan(3) = 71.57°\); \(\arctan(2) + \arctan(3) = 63.43° + 71.57° = 135° \), and we know that \(cos(135°) = -\frac{1}{\sqrt{2}} \). So we got it right.
There was one more problem in this series:
Trig(double inverse trig)
How do I simplify this: sin(2 arccos x)
What I did was I solve it in terms of cos, so
sqrt(1 – (cos(2 arccos x))^2)
so I’ll have sqrt(1 – 4x^2).I have a bad feeling about this.
Doctor Fenton took this one:
You are on the right track by using a trigonometric identity to simplify the problem, but you have to be careful not to make up your own identities. You have rewritten the given expression in terms of cos(2 arccos(x)), but in evaluating cos(2 arccos(x)), you seem to assume that
cos(2 arccos(x)) = 2 cos(arccos(x)),
which is not correct.
Let θ = arccos(x), so that cos(θ) = x. Then you should know that cos(2θ) is not the same as 2 cos(θ). There is an identity which expresses cos(2θ) in terms of sin(θ) and cos(θ), and you need to use that to evaluate cos(2θ). You know that cos(θ) = x, and the first identity you used will give you the value of sin(θ) when cos(θ) = x.
The student got it:
Oh! Oh! So my starting equation will be sqrt(1 – cos(2 arccos x)^2)
Let θ = arccos x. So x = cos θ, and the expression is
= sqrt(1 – (cos 2θ )^2)
= sqrt(1 – (cos^2 θ – sin^2 θ )^2)
Then I notice that sin^2 θ can be equal to 1 – cos^2 θ .I LITERALLY SCREAMED THE MOMENT I NOTICED THAT!! I FEEL VICTORIOUS!!!
= sqrt(1 – (1 – 2 cos^2 θ )^2)
= sqrt(1 – (1 – 2 cos^2 θ – 2 cos^2 θ + 4 cos^4 θ ))
= sqrt(4 cos^2 θ – 4 cos^4 θ )
= sqrt(4 cos^2 θ )(sqrt(1 – cos^2 θ )) = 2 cos(arccos x)(sqrt(1 – (cos(arccos x))^2)
My final answer is…(drum roll please)
Tada!!
2x sqrt(1 – x^2)
They say calculus is difficult! I say… yeah it’s difficult. Haha
He had continued the way he originally started, rewriting as a cosine in the expectation that that would work better with the arccos; this was more complicated than it had to be.
Doctor Rick jumped in with a comment:
You solved it! Good work.
You did it rather backward from what I’d do, but there is nothing wrong with that. We’ve probably already said that most good math problems can be solved in multiple ways.
My method, perhaps more direct, uses the double-angle identity for the sine. We have x = cos(θ), and we want to find sin(2θ) = 2 sin(θ) cos(θ). We just need to write sin(θ) = sqrt(1 – x^2) and we’re done.
However, we really should consider that sin^2(θ) = 1 – x^2 also has the solution sin(θ) = – sqrt(1 – x^2). Are we sure that our solution doesn’t need a negative sign? The fact is that we don’t need it; we can show this based on the fact that arccos(x) is in quadrant 1 or 2.
This is similar to what happened above with a cosecant; that, and the sine, are positive for the entire range of arccos, which keeps things simple. In other problems, this warning about the sign might be important.
So we have gone through a good list of problems combining trig functions and their inverses. There are probably several more types we could look at, but this will do.

Pingback: Subtleties of Inverse Trig Functions – The Math Doctors
Pingback: More On Mixing Trig Functions – The Math Doctors
Pingback: Pitfalls of Inverse Trig Functions – The Math Doctors