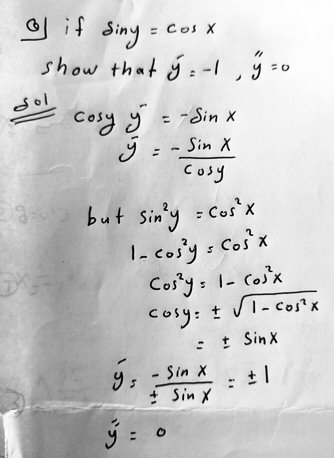I’ve had several occasions in face-to-face tutoring lately to refer to a past post on mixing (that is, composition) of trig and inverse trig functions. Several recent questions have touched directly or indirectly on this same general idea and extended it, so I thought I’d post them.
Converting an angle?
The first, in mid-October, is from Simran:
Hello math doctors,
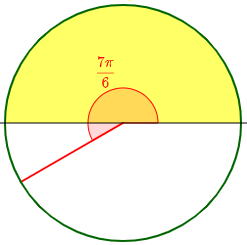
Is there a method for changing angles and converting them to the desired quadrant angle. For example, if I want to change 7π/6 to an angle that lies between 0 to π then is there any sort of trick. I am able to do it for angles less than π but not for higher angles. Would be glad to know if there are any methods!
The angle \(\frac{7\pi}{6}\) is in the third quadrant; what could it mean to convert it to an angle in the first or second quadrant (as shown in yellow)?
I asked for clarification, suggesting a likely context:
Hi, Simran.
It depends on what you mean by “convert”. If an angle is not in the desired quadrant, then you can’t make it so.
I imagine you might be trying to find an angle in the interval [0, π] for which the cosine is the same as for the given angle 7π/6. It will not be a coterminal angle; and if you wanted the same value of the sine, you would need a different interval, as the sines over that interval are all non-negative.
Please tell us the context of your question, so we can be sure what you really want to do.
My suggestion is that we are trying to find \(\cos^{-1}\left(\cos\left(\frac{7\pi}{6}\right)\right)\), that is, the angle in \([0,\pi]\) whose cosine is the same as the cosine of \(\frac{7\pi}{6}\):
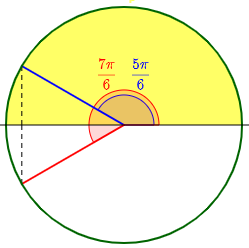
The alternative problem would be \(\sin^{-1}\left(\sin\left(\frac{7\pi}{6}\right)\right)\), which asks for the angle in \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\) whose sine is the same as the sine of \(\frac{7\pi}{6}\):
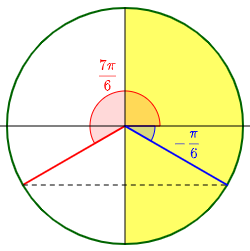
We’ll be coming back to these problems.
Inverse trig(co-trig)
Now he told us different problem, similar to what I had guessed:
Yes, I meant finding a desired angle in the following ranges for example: sin-1(cos 33π/5) how do I convert 33π/5 to a range that satisfies sin-1 .
This is a different angle, and a different interval, but the same type … almost.
Now I was able to answer:
Thanks. So you are asking something similar to what I suggested.
This is a case I didn’t get into in
Mixing Trig and Inverse Trig Functions
where I would have described it as “inverse trig(other trig)“, or perhaps more specifically as “inverse trig(co-trig)“.
In finding sin-1(cos(33π/5)), we want to
find the angle θ in [-π/2, π/2] such that sin(θ) = cos(33π/5).
In the old post, we looked briefly at cases I called
- “trig(inverse trig)” (e.g. \(\cos\left(\cos^{-1}\left(\frac{3}{5}\right)\right)\)),
- “inverse trig(trig)” (e.g. our \(\cos^{-1}\left(\cos\left(\frac{7\pi}{6}\right)\right)\) above), and
- “trig(other inverse trig) (e.g. \(\csc\left(\cos^{-1}\left(\frac{3}{5}\right)\right)\)).
We’ll look at one of these below, in a little more detail than before.
But this is one we didn’t look at there:
- “inverse trig(other trig)”: \(\sin^{-1}\left(\cos\left(\frac{33\pi}{5}\right)\right)\).
In the most general case, there is no shortcut for this type; you’d just have to evaluate it with a calculator. But when the two trig functions have the right sort of relationship, something can be done. I called this one “inverse trig(co-trig)” because the outer function is the inverse of the cofunction of the inner function, and cofunctions are related via the angle itself, which gives us some useful tools. Specifically, \(\cos(\theta)=\sin\left(\frac{\pi}{2}-\theta\right)\).
I would probably start by moving 33π/5 to the interval [0, 2π] in the sense of finding a coterminal angle (since a trig function of a coterminal angle is the same as for the original angle).
I do this by subtracting an appropriate multiple of 2π; to find this, I convert 33/5 to the mixed number 6 3/5, so I know that subtracting 6π will accomplish the goal. My coterminal angle is 6 3/5π – 6π = 3π/5.
This changes the problem to
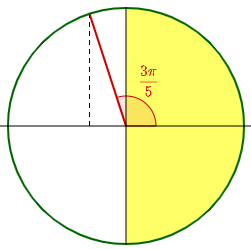
Find the angle θ in [-π/2, π/2] such that sin(θ) = cos(3π/5).
So we’ll be looking for an angle in the yellow zone whose sine is the same as the cosine of this angle:
But since I know that cos(x) = sin(π/2 – x), this is equivalent to
Find the angle θ in [-π/2, π/2] such that sin(θ) = sin(π/2 – 3π/5) = sin(-π/10).
And since -π/10 is in the required interval, that is the answer.
(Checking, I find that sin-1(cos(33π/5)) = -0.314159…, and -π/10 = -0.314159… .)
Here is the answer, which in effect reflected our angle around the bisector of the first quadrant:
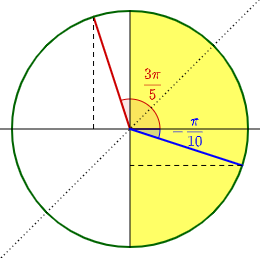
At a couple points this was easier than it could have been.
A more complicated example
Let’s try a harder one: \(\sin^{-1}\left(\cos\left(-\frac{22\pi}{5}\right)\right)\).
First, we want to find a coterminal angle for \(-\frac{22\pi}{5}\) that will in \([0,2\pi)\), just to get it in the right ballpark. We see that \(-\frac{22}{5}=-4\frac{2}{5}\). If we add \(6\pi\) to \(-\frac{22\pi}{5}\), we get \(\frac{8\pi}{5}\), which is in quadrant IV. (Or we could, instead, add \(4\pi\) and get \(-\frac{2\pi}{5}\).)
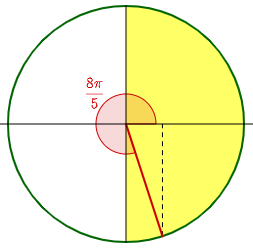
Now we want to find the angle in \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\) whose sine is the same as the cosine of \(\frac{8\pi}{5}\), which is the sine of \(\frac{\pi}{2}-\left(\frac{8\pi}{5}\right)=-\frac{11\pi}{10}\).
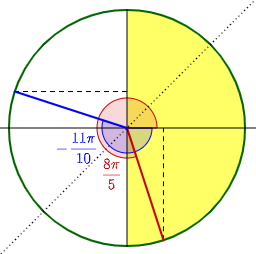
This angle itself is in the second quadrant, not the first or fourth; its sine is negative, so we need to find an angle in quadrant IV with the same sine. We need to reflect it across the y-axis, which we can do by subtracting it from \(\pi\): \(\pi-\left(-\frac{11\pi}{10}\right)=\frac{21\pi}{10}\). Finally, subtracting \(2\pi\) from this, we get an answer: \(\frac{\pi}{10}\).
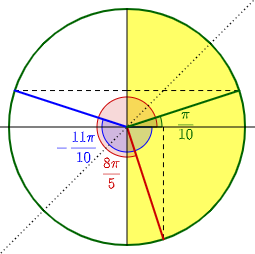
Checking again, we find that \(\sin^{-1}\left(\cos\left(-\frac{22\pi}{5}\right)\right)\approx0.314159\), and \(\frac{\pi}{10}\approx0.314159\).
Inverse trig(trig)
Now let’s try the problem I suggested in response to your original question:
cos-1(cos(7π/6)) = ?
Find the angle in the interval [0, π] for which the cosine is the same as for the given angle 7π/6.
This type is covered in the post I mentioned, under “Inverse trig(trig)”.
Here I would use the fact that cos(-x) = cos(x); that is, two angles have the same cosine when they are coterminal with an angle and its negative. In particular, since we want both to be positive angles, we can add the period to the negative one:
cos(2π – x) = cos(x)
So the angle we want is 2π – 7π/6 = 5π/6.
(Checking again, I find that cos-1(cos(7π/6)) = 2.61799…, and 5π/6 = 2.61799… .)
These probably don’t cover everything that can happen, but illustrate the kinds of thinking required.
This is far more conventional. I used the fact that the cosine is an even function, symmetrical about the angle 0, in what I called in the other post “the second Grant’s Tomb twist”.
Simran responded,
Thank you, I tried something similar in exams but couldn’t get it totally, now it’s more clear. That tomb joke took me a while to understand!!
I answered,
Yes, it’s a very American joke!
If you have more problems of this sort, feel free to share them, as each one can be very different, and need a slightly different perspective.
Simran closed:
Sure! I will do that, in fact I am trying some new ones lately (they made me realise I need to brush up my trigo skills!)
We haven’t heard more yet.
Differentiating sin(y) = cos(x)
Two days earlier, Amia had asked a calculus question that would eventually lead us into a related issue:
Hi Dr math,
I want your opinion for the question and its solution in the attached,
The problem is one of implicit differentiation; the derivative, surprisingly, is a constant, which implies that the graph is a straight line. But Amia got two constants rather than one. Is the work correct?
Doctor Rick answered, correcting the problem, and confirming the answer with an alternative method:
Hi, Amia.
You did not prove exactly what the problem says to prove, but what it says to prove is not true. Perhaps you just have a typo in the problem statement, and it should say:
if sin y = cos x, show that: y’ = ±1, y” = 0.
This can also be proved without calculus (until the last step, where obviously we need to bring in the derivative). Using the identity
cos x = sin(π/2 – x)
and familiar methods for finding all solutions of a trigonometric equation, you can get a family of solutions for y in terms of x. Graphing that family of functions will tell you more than what the problem asks for. I think it’s worth doing.
The suggestion is to use the cofunction identity in a way that is similar to our work above, finding \(\sin^{-1}(\cos(x))\) (but not restricting the result to the range of the inverse sine).
Amia replied showing the suggested method in action:
sin y = cos x
= sin (pi/2 + x) = sin (pi/2 – x)
y = pi/2 ± x + 2pi n
dy/dx = ±1
The two different signs, as I understand it, arise from the evenness of the cosine.
Doctor Rick replied,
Your solution is correct, but the way you have written your work makes it appear that you think:
if sin a = sin b then a = b + 2πn, for some integer n.
That is not entirely correct. Instead,
if sin a = sin b then a = b + 2πn or a = (π – b) + 2πn
We’ll examine this claim below.
Here is what I did:
sin y = cos x
sin y = sin(π/2 – x)
y = (π/2 – x) + 2πk, k ∈ ℤ, OR y = π – (π/2 – x) + 2πk, k ∈ ℤ
y = –x + (π/2 + 2πk) OR y = x + (π/2 + 2πk)
y = ±x + (π/2 + 2πk), k ∈ ℤ
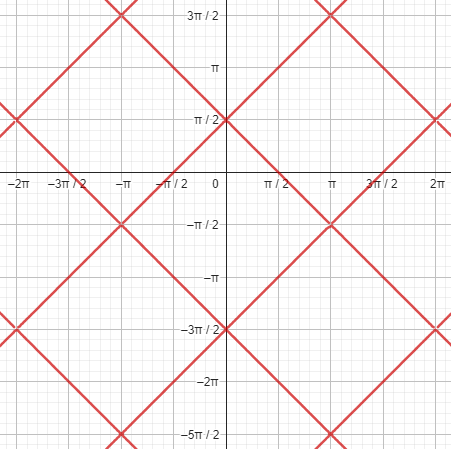
Thus the solution is two families of parallel lines, one with slope 1 and one with slope –1.
The implicit differentiation hid this structure, by not showing that each sign corresponds to a different kind of point on the graph. (But at some points, the graph has both derivatives! Clearly it is not a function.)
Letting GeoGebra do the graphing of the original equation, I get:
Here is a graph of \(\sin^{-1}(\cos(x)\), which restricts the range:
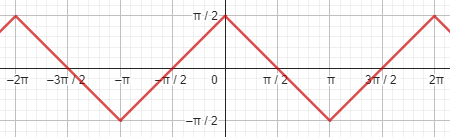
Notice that, if the original problem restricted x to \((0,\pi)\), and y to \((-\frac{\pi}{2},\frac{\pi}{2})\), the answer of \(y’=-1\) would be correct.
All solutions of sin(y) = sin(x)
A little later, Amia submitted a new question following up on that by asking for proof of Doctor Rick’s claim:
Hi Dr math ,
I have this question:
If sin x = sin y
then x = y+2 pi n
or x = pi – y + 2 pi n
How can I be sure that the solutions above are all the solutions?
I answered, hoping to provide a different perspective:
Hi, Amia.
It may be helpful if you can tell us why you are not sure. What part of this do you understand, and what part do you not? And what kind of answer would satisfy you?
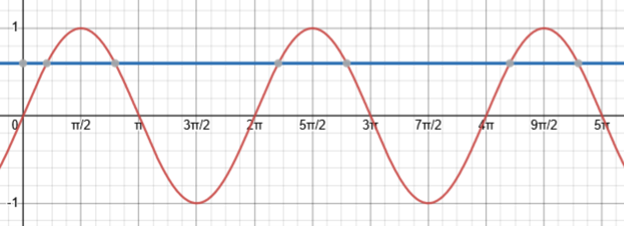
As I see it, the equation asks you to determine all angles y that have the same sine as a given angle x (or vice versa). This can be answered in terms of the unit circle definition of the sine, or an understanding of the graph of the sine function, or by considering intervals over which the sine function is one-to-one.
By the unit circle definition, we can see that any two angles with the same sine, within the same cycle, must be supplements:
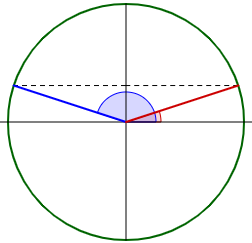
If one angle is \(\theta\), the other is \(\pi-\theta\).
For example, just consider this graph:
If -π/2 ≤ x ≤ π/2, all the values of y are either x plus an integer multiple of the period, 2π, or (π – x) plus an integer multiple of the period, 2π. If x is not in that interval, you might first subtract a multiple of the period to bring it into that interval, and apply the same reasoning to that.
This fills in the background of the previous question.