(A new question of the week)
Having discussed trigonometric identities on Monday, let’s make this Trig Week, by looking at a discussion from two months ago in which we were asked about alternative routes to a proof.
Here is the question:
I have been trying to prove this trigonometric identity: \(\displaystyle\frac{\tan\theta + \sec\theta\ – 1}{\tan\theta\ – \sec\theta + 1} = \frac{1 + \sin\theta}{\cos\theta}\)
My textbook proves it using two different methods.
Now, I made an attempt to solve this question in a different way.
I have somehow reached at this step
L.H.S. = \(\displaystyle\frac{\tan\theta + \sec\theta\ – 1}{\tan\theta\ – \sec\theta + 1} = \frac{\sqrt{1+\sin\theta}}{\sqrt{1-\cos\theta} }\cdot \frac{\sqrt{1+\sin\theta} – \sqrt{1-\sin\theta}}{\sqrt{1+\cos\theta} -\sqrt{1-\cos\theta}}\)
But, I am stuck at this position. Please help me to solve it further.
Please tell, how can I prove that
\(\displaystyle\frac{\sqrt{1+\sin\theta}}{\sqrt{1-\cos\theta} }\cdot \frac{\sqrt{1+\sin\theta}\ – \sqrt{1-\sin\theta}}{\sqrt{1+\cos\theta} -\sqrt{1-\cos\theta}} = \frac{1 + \sin\theta}{\cos\theta}\) ?
I also want to know one more thing,
By how many different methods can a single trigonometric identity be proved? (one, two, or infinitely many)
I will be thankful for help!
The book’s first method “magically” replaces 1 with \(\sec^2\theta – \tan^2\theta\) (one of the Pythagorean identities). This might be something a really smart person would see as a good idea, by looking ahead and seeing what use could be made of it; but it isn’t obvious! We’ll see later how it might have been invented.
The second method uses what must be an identity the author had seen previously and thought worth remembering: \(\displaystyle\sec\theta + \tan\theta = \frac{1}{\sec\theta\ – \tan\theta}\). This would normally be an exercise in itself. (See if you can prove it! There is a quick, insightful way, and several long slogs.) So, again, someone with a lot of experience might think of this; but even then it isn’t clear why they would.
So it is very reasonable for Navneet to want to find a more natural proof.
Doctor Rick replied, first checking whether Navneet’s intermediate expression was correct, rather than just trusting it and proceeding from there:
The first thing I want to do is to check whether the identity you’re proposing is really true — it’s a waste of time to try to prove something false. So I made a graph of each side:
What you see is that the two functions are equal only in the first quadrant, that is, when both sin θ and cos θ are positive. I don’t know what you did, but perhaps you did something similar to replacing cos θ by √(1 – sin2 θ), which is not true for θ in quadrant 2 or 3.
On an exam, a student (probably) couldn’t do this graphing check, but it can be very useful in real life. When part of the graphs coincide, as above, we can see that the supposed identity is valid only on part of the domain, which supports Doctor Rick’s suggestion. If Navneet had shown his steps, we could have looked for the specific error, but this seems to be a likely explanation. It can be very easy to forget that an identity has to be true for all angles, not just in quadrant 1.
As a general heuristic rule, if I saw my expressions getting as complicated as yours, I’d look for a different approach.
[“Heuristic”, as used here, means a “rule of thumb” – a method of problem-solving that is not guaranteed to work, but is supported by experience. I just discovered, in looking it up, that the word comes from the same root as “eureka”, which is Greek for “I have found/discovered it”. In general, heuristics are guides to finding answers by thoughtful exploration, or by practical rather than formulaic means.]
How many different proofs of a given identity are there? I have no idea. You may have seen this list of 121 different proofs of the Pythagorean Theorem:
Pythagorean Theorem and its Many Proofs – Bogomolny
There is no reason to suppose that no further proofs could be found. Likewise, I’d expect any interesting trig identity to be susceptible to more than one method of proof, with no necessary limit on how many there are. (We have often emphasized to students that there isn’t just one correct method for solving a math problem.)
This identity is complicated enough that it could probably be given to a class, and every student might find a (slightly, or entirely) different way.
Lacking steps to correct, and wanting to show how to find a better way, Doctor Rick next showed his own thinking. My Monday post included heuristics like converting to sines and cosines; but if you are observant, you can often see shortcuts:
Often in trying to prove a trig identity, I will start by putting everything in terms of sine and cosine, just so I have a more restricted set of identities to remember and try to apply. That would make for a different method than either of those in your book, though at some level it might be closely related to one of them.
My question, looking at the two proofs, is: How in the world would a student be expected to come up with either one? They involve some pretty tricky insights. I think it would be better to show how such a proof can be discovered, rather than merely to show the final proof. So let me show you how I would approach the proof myself.
Despite what I said about converting everything to sine and cosine, in this case I noticed something about the RHS first:
(1 + sin θ)/cos θ = 1/cos θ + sin θ/cos θ = sec θ + tan θ
So now I have both sides in terms of tangent and secant. Let’s run with that!
Now, I’m going to do something that is often considered wrong in the final proof — but even if your teacher considers it wrong, it’s OK to do in the exploration phase. (But see Proving Trig Identities vs. Solving Trig Equations where Dr. Peterson explains that it isn’t really wrong, if done right.) What I’m talking about is working with the identity as a whole, as if it were an equation you were solving.
This link is one of those I showed on Monday.
We have the equation (not yet proven to be an identity, so I’ll write =? instead of =):
tan θ + sec θ – 1
———————– =? sec θ + tan θ
tan θ – sec θ + 1Multiply through by the denominator:
tan θ + sec θ – 1 =? (sec θ + tan θ)(tan θ – sec θ + 1)
tan θ + sec θ – 1 =? (sec θ + tan θ)((tan θ – sec θ) + 1)
tan θ + sec θ – 1 =? (tan2 θ – sec2 θ) + (tan θ + sec θ)
tan θ + sec θ – 1 =? (tan2 θ – sec2 θ) + (tan θ + sec θ)
tan θ + sec θ – 1 = -1 + (tan θ + sec θ)Voila! On the last line, the two sides are identically equal. All we have to do now is to confirm that each step I took is reversible, and/or rewrite the work so that it starts from the LHS of the putative identity and ends up at the RHS. When you do the latter, you will have one of the book’s two methods.
It often happens that a mathematician first discovers a proof by “iffy” methods such as this, and later reworks it so that it is more “elegant”. When they then publish the final result, the path by which they discovered the proof is hidden; it looks like magic, or incredible insight (like this book’s two proofs). As Doctor Rick said, “I think it would be better to show how such a proof can be discovered, rather than merely to show the final proof.” This would be good advice for many authors. (Textbook authors commonly do try to communicate more clearly; but even they often aim too high, due to the “curse of expertise”, by which they have difficulty seeing what they write from a beginner’s perspective. I’m sure we sometimes do the same, not knowing much about the people who write to us; but we have the advantage that we can have a conversation, learning about the student’s own needs. The same is true of face-to-face tutoring.)

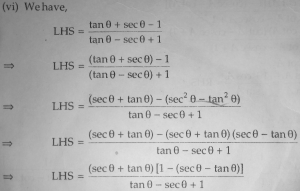

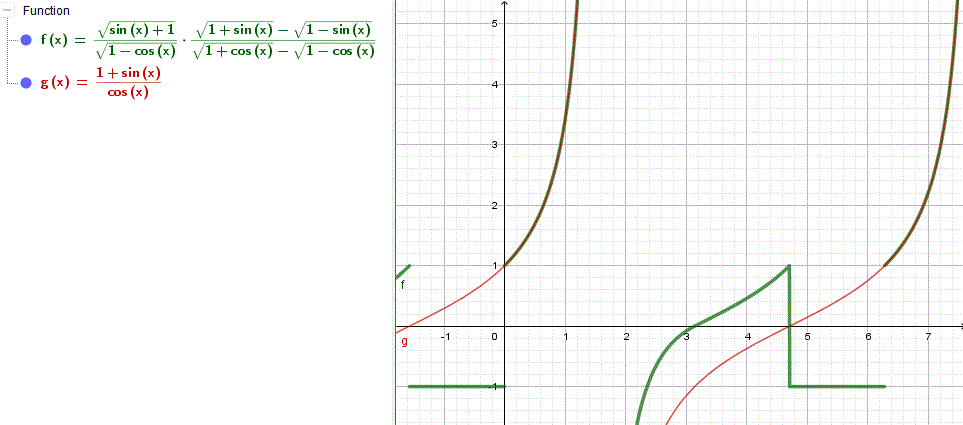
Pingback: The Art of Proving Trig Identities – The Math Doctors
Pingback: A Challenging Triangle Trigonometry Problem – The Math Doctors