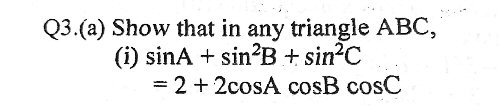(A new question of the week)
Trigonometry identities can be hard to prove, and more so when they are specifically about a triangle.
A (flawed) identity for triangles
The question came from Eli, in early September:
I usually enjoy trigonometry, but not when it comes to trigonometry involving triangles. It has always been a gamble with those kinds of questions. Maybe there’s information I am missing? Or perhaps I am looking at it the wrong way? The challenge comes with the numbers [problems] concerning proofs. In this particular number, I can’t find a way to proceed from where I stopped. For context, I have covered trigonometry in the class (compound angles, double angles, r formula, t formula, factor formula).
(A small note on terminology: It took me a while to see what “number” means here; evidently in his culture, what I would call a “problem set”, consisting of multiple “exercises”, is called an “exercise”, consisting of multiple [problem] “numbers”. I have long been interested in variations both in language and in math; here I also don’t know what is meant by “r formula” and “t formula”! If it mattered, I’d just ask for the definitions.)
We can see that Eli started with the left-hand side of the equation, and used the fact that each angle is the supplement of the sum of the other two to try to write in terms of cosines. The work is wrong, but since, as we’ll see in a moment, the problem itself is wrong, I won’t try to elaborate on it.
Correcting the problem
Doctor Rick answered:
Hi, Eli, glad to hear from you again.
I think the problem here is that the problem has a typo! I haven’t tried to solve it yet, but I noticed that the RHS is symmetric under interchange of A, B, and C while the LHS is not, and this seemed odd. So I tried some random angles in a spreadsheet and my hunch was right: the equation is not an identity as it stands. If you square sin A (as sin B and sin C are squared), then it appears to be an identity.
sin2 A + sin2 B + sin2 C = 2 + 2 cos A cos B cos C
Give the corrected problem a try! I will, too.
How do you recognize an invalid identity? In this case, it just felt wrong because the variables are almost treated identically; the lack of a square on \(\sin A\) messed up the symmetry, and trying specific values showed that it was not an identity. We will often do quick checks like this when a problem is particularly complicated, to make sure it is correct.
As a simple example of the check, suppose we have an equilateral triangle, so that \(A=B=C=60^\circ\). Then the LHS is $$\sin60^\circ+\sin^2 60^\circ+\sin^2 60^\circ=\frac{\sqrt{3}}{2}+\frac{3}{4}+\frac{3}{4}=\frac{3+\sqrt{3}}{2},$$ while the RHS is $$2+2\cos60^\circ\cos 60^\circ\cos60^\circ=2+2\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)=2\frac{1}{4}=\frac{9}{4}.$$ These aren’t equal, so it can’t be right. On the other hand, the new LHS gives the right value: $$\sin^2 60^\circ+\sin^2 60^\circ+\sin^2 60^\circ=\frac{3}{4}+\frac{3}{4}+\frac{3}{4}=\frac{9}{4}.$$
(For other wrong problems, the error might show up in only some cases, so making a spreadsheet was a good idea. Other times, we might graph both sides of a claimed identity for the same purpose.)
So here is the correct problem, through the magic of picture editing:
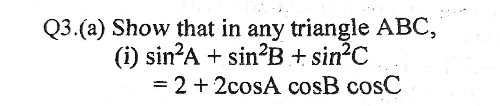
A couple hints
Eli replied,
Hello! Typo or not, it seems I don’t know what I’m doing when it comes to these kinds of proofs. I have tried the cosine rule and the Hero’s formula and instead i am getting further and further away from the answer. Maybe I need a nudge in the right direction or a subtle hint but the feeling is frustrating. Thank you for your time;)
I suspect part of the frustration comes from having worked on an invalid problem, so that it seems as if all the easy methods have already been tried.
The “cosine rule” relates angles to sides, and “Hero’s formula” finds the area of a triangle given the sides; neither really ought to be needed, because the problem doesn’t involve the sides. But sometimes a problem that doesn’t directly involve the sides of a triangle nevertheless does depend on them, so it is not wrong to try this. It’s a last resort, though, and doesn’t help.
Doctor Rick responded, focusing not on what went wrong, but on what went right:
This problem is a tough one, I agree! It’s not obvious what to do; you have thought of several different tools you could use — A + B + C = 180°, with an angle-sum identity; the Law of Cosines; and Heron’s formula for the area of a triangle. You’re right, everything seems only to make things more complicated. But let’s look for some helpful things in your work.
I see that you rewrote the LHS in terms of cosines, to match what we have on the RHS. That seems like a good idea, even if the Law of Cosines doesn’t turn out to be helpful. Have you written out the full equation that we then want to prove is an identity?
3 – cos2 A – cos2 B – cos2 C = 2 + 2 cos A cos B cos C
1 = cos2 A + cos2 B + cos2 C + 2 cos A cos B cos C
As we’ll discuss below, treating an identity as if it were an equation to solve can be problematic, but it’s a good thing to try, at least as an exploration, when other things don’t work.
Using the fact that A + B + C = 180° is the simplest idea, but I don’t see that you have used it in the best way. Have you tried using it to eliminate one of the three variables? Say you eliminate C; then the resulting equation in A and B ought to be an ordinary trig identity — true for any angles A and B. (We really only need it to be true for positive angles such that A + B < 180°, but my guess is we’ll be able to prove it for all angles.)
The trouble with this idea is that we will reintroduce sines when we apply the angle-sum identity. But it’s worth a try — any sines that are squared can again be converted into cosines if necessary, and some terms may cancel.
So try this approach. I tried it just now, and it worked!
What we are to prove depends on A, B, and C being interior angles of a triangle; by using the fact about their sum, we are merging that condition into the equation, making what we hope is an unconditional fact out of a conditional fact. That brings the problem into the realm of ordinary identities, which a student will have more practice with (just as Eli mentioned at the start!).
Success … and a concern
Eli wrote back:
I did get the answer as well when I considered the whole identity and used the sum of interior angles of a triangle. The problem is that it doesn’t look like a proper proof (RHS = LHS). I just end up with 1 = 1 which is true but I’m not sure it is what we were trying to prove initially. Is there a way we could bring back the original identities on the left and right hand side?
Here is the work, made a little more readable and explained:
$$1=\cos^2A+\cos^2B+\cos^2C+2\cos A\cos B\cos C\\\\1=\cos^2A+\cos^2B+(-\cos(A+B))^2+2\cos A\cos B(-\cos(A+B))\\\\1=\cos^2A+\cos^2B+\cos(A+B)(\cos(A+B)-2\cos A\cos B)\\\\1=\cos^2A+\cos^2B+(\cos A\cos B-\sin A\sin B)((\cos A\cos B-\sin A\sin B)-2\cos A\cos B)\\\\1=\cos^2A+\cos^2B+(\cos^2A\cos^2B-2\cos A\cos B\sin A\sin B+\sin^2A\sin^2B)-2\cos^2A\cos^2B+2\sin A\sin B\cos A\cos B\\\\1=\cos^2A+\cos^2B-\cos^2A\cos^2B+\sin^2A\sin^2B\\\\1=\cos^2A+\cos^2B-(\cos A\cos B)^2+(\sin A\sin B)^2\\\\1=\cos^2A+\cos^2B-(\cos A\cos B+\sin A\sin B)(\cos A\cos B-\sin A\sin B)\\\\1=\cos^2A+\cos^2B-\cos(A-B)\cos(A+B)\\\\1=\cos^2A+\cos^2B-\frac{1}{2}(\cos(2A)+\cos(2B))\\\\1=\cos^2A+\cos^2B-\frac{1}{2}((2\cos^2A-1)+(2\cos^2B-1))\\\\1=\cos^2A+\cos^2B-\cos^2A+\frac{1}{2}-\cos^2B+\frac{1}{2}\\1=1$$
Several steps are not what I would have done … but as I tell students, the right method is the one you see, in contrast to the one you don’t see.
Doctor Rick was ready for the concern about the form of the proof:
I had wondered if this would be the next point to discuss. My proof is not the same as yours at all points, but it is similar, proceeding as if we were solving an equation rather than proving an identity; I too ended up with the tautology 1 = 1.
This can be a valid way to prove an identity, as long as all the steps are equivalences (that is, we could run the steps backward — a given line is true if and only if the line before it is true). You will benefit from reading this Math Doctors blog:
Different Ways to Prove a Trigonometric Identity
See especially the sections “Can you work on both sides?” and “When a ‘bad’ proof is valid”.
This issue comes up a lot!
Many teachers do require that you work “from one side to the other”. But that is really pretty much what you have done; you just haven’t quite written it that way.
We have already established that the proposition to be proved is equivalent to the identity
sin2 A + sin2 B + sin2 (A+B) = 2 – 2 cos A cos B cos (A+B) for all angles A, B. [1]
A purist might say that once we have this, we’ve got to work from one side to the other. But I see nothing wrong with first showing (as I had already led you to do) that [1] in turn is equivalent to
cos2 A + cos2 B + cos2 (A+B) – 2 cos A cos B cos (A+B) = 1 [2]
From this point on, we work with the left side only, transforming it step by step until we get 1. So we’d start like this:
cos2 A + cos2 B + cos2 (A+B) – 2 cos A cos B cos (A+B) =
cos2 A + cos2 B + cos (A+B)(cos (A+B) – 2 cos A cos B) =
cos2 A + cos2 B + (cos A cos B + sin A sin B)(cos A cos B + sin A sin B – 2 cos A cos B) =
…
Do you see how this does exactly what you did, but is in the “proper” form?
It didn’t take much to “correct” the work.
Eli replied:
Thank you for all your help. Now I just have to convince my teacher that the proof is valid.
Doctor Rick said,
Again, the point is that we prove that the equations
sin2 A + sin2 B + sin2 (A+B) = 2 – 2 cos A cos B cos (A+B) [1]
and
cos2 A + cos2 B + cos2 (A+B) – 2 cos A cos B cos (A+B) = 1 [2]
are equivalent: that any solution of one is a solution of the other. Thus, if we can show that [2] is true for all values of A and B, then we have shown the same for [1]; and this is the definition of an identity. You have a proof of [2] in the standard form, so you’re done.
If this concept of equivalent equations is not familiar to you, take a look at our blog:
Principles for Solving an Equation
See the section halfway down, “The importance of equivalent equations.”
If your teacher insists that you write a proof of [1] by working from one side to the other, it should be possible to rework your proof into that form, as Doctor Peterson showed for one example in the blog I pointed you to earlier. Let me know if you need help with that.
(Your teacher does know that the problem had a typo, right?)
How can I learn to solve problems faster?
The next day, Eli moved on to more general questions:
Hello! I’ve gone through the page about twice now. I like the arguments for working with both sides and transforming it into the ‘proper’ form.
My only worry is that all the methods described take a lot of time. Even some of the steps like expressing everything in terms of cosines and sines. I worry about time not because I like a rushed answer but because I’m meant to work on each problem in under 6 minutes in an exam. I have personally resorted to some of the steps in the blog but as a last resort because I’ve been trained to get solutions in the shortest time possible. An example would be if I saw that my RHS is in terms of cotangents and tangents, I would try my best to transform everything on the left side to that using any identity that comes to mind. On other occasions I would try the Demoivre’s theorem (or literally anything to cut my time in half). Stopping to first convert everything to sines and cosines in this case would obviously work but it would take a very long time better spent on other problems (which is why I do trig last). I refer to these steps as a necessary step backward in order to go forward. (When I don’t know how to proceed to the next step, I usually use the cosines and sines method.)
I’ve had this question fora while now so I’m going to ask. How to take less time on a trig proof. How to see that your proof is headed nowhere. For now I will attempt to rework the proof into the desired form, and I intend to solve the remaining 30 problems under trig proofs or die trying.
I have to say that this sort of speed test is totally foreign to me. This is yet another cultural difference (Eli appears to live in Uganda); we do hear from many students in various countries with this sort of high-pressure exams, presumably for highly competitive universities, and frankly we don’t have much to say about it. I’d like to know whether this produces better students, or only students who are afraid to take time to think creatively.
Doctor Rick responded,
I am not a good one to talk with about “speed math”! I am the slow and methodical type, not really good at seeing quick ways to do things, except maybe after I’ve found the slow way!
You’re doing it the way I would, and I don’t see a better way. If some idea jumps out at you, give it a try; if not, try some tricks that have worked in the past; and if all else fails, try the sines-and-cosines approach that is often tedious but likely to work eventually.
For contest-level problems, you would often need outside-the-box ideas (like DeMoivre), taking the problem into an unexpected branch of math; with that kind of problem, the standard methods would generally be so tedious that they aren’t worth trying. I can’t do such problems in 6 minutes, but then I hope they wouldn’t be on your exam.
Are exam problems generally as difficult as the exercises you are working on? Perhaps you are worrying unnecessarily. In any case, please don’t die trying! It isn’t worth it. 😉
Do you have another problem from this set that I could try?
Contests (at high levels, at least) are designed to identify the very best students, requiring very creative thinking; speed is generally not the main criterion, though it may help.
A few days later, Eli tried another problem himself:
Hello Doctor Rick, it’s been a while. I decided to complete the trig exercise [set]. (Most of the numbers were okay, and the page on this site concerning proofs did help.) The exams do have the harder questions for certain topics. They will often set harder trig numbers [problems]. Usually one of them is just solving for an unknown, so that one isn’t a problem (05 marks for 3 minutes of your time). The other is 12 marks divided into two to three parts for 6 marks each part. It’s where we can find challenging proofs (sadly the second part depends on whether you passed the first). We are given options though, so you do not have to die with trigonometry, but it’s so satisfying to have that option, especially since I often do them quicker than the others. The other relatively simple topics where they set harder problems are further geometry (conic sections) and differential equations (specifically mathematical models). I think I have a relatively good grasp of everything, but get very frustrated when I find problems I can’t solve. This is very triggering during an exam and can end up hurting performance if it happens at the start. The teachers do not really mind what order we do the numbers, so we are free to do it however we want. It’s funny how often we use Demoivre’s theorem (Usually the easier, more sought out problems concern complex numbers), so when you say contest maths, it seems strange to me. Anyway that’s my curriculum.
I used one of the tools on your website for this number below. Did I use it correctly?
Doctor Rick concluded:
Yes, your work looks good. You worked “from both ends toward the middle”, then reversed part of that work to “drive across the bridge” from one side to the other in the standard identity-proof style. I might have chosen to do more on the RHS, putting it in terms of 2θ rather than 4θ so that it would look more like the LHS, but as you did it, you recognized the expressions from the double-angle identities without difficulty.
There are commonly many ways you could approach a proof like this, depending on what you happen to see. In this case, when I tried it without looking a Eli’s answer, I found that I did exactly what he shows as the final form, because I recognized that multiplying the numerator and denominator of the LHS by the conjugate of the denominator would lead in a useful direction (namely, toward a double-angle formula), and saw another arising in the result. The more problems you have tried, the more insight you are likely to have; but there is never a guarantee that you will see the best way.