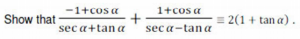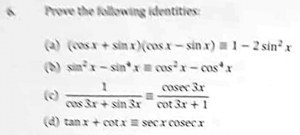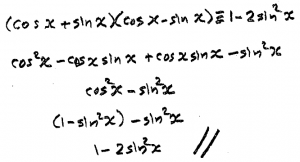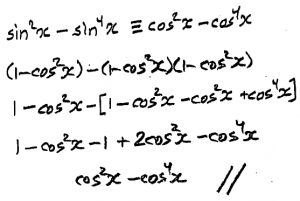(A new question of the week)
Last week we looked at a recent question about basic trigonometric equations. That discussion continued into the subject of identities, which we’ll look at here. We’ll be sitting in on an extended chat about many important aspects of this kind of work. It’s still very long, even after extensive editing, but worth reading through.
How do I get there? Practice!
Picking up the thread, here is Sarah’s new question:
How do you prove an identity?
Doctor Rick picked up the discussion:
Finding a way to prove an identity is something of an art form, learned by practice. Here is an example of a more or less general approach to proving trig identities, which won’t always give the shortest or most elegant proof, but at least it’s a backup:
Proving Trigonometric Identities
Again, you can search the Archive for the words “trig identity proof” to get suggestions for many specific proofs.
If you would like to present a specific example of a trig identity to be proved, we will be happy to work through the details with you.
Sarah answered:
My problem is that after l see the answer, l get it, but I’m not capable of getting to the answer myself, and I’ve been getting a lot of practice. Usually, my mathematical intuition and recognition is quite good, not sure where that went.
I’m attaching some examples:
If you are not familiar with the “triple-equal” symbol “≡”, it means “is identically equal to”, that is, “is equal to, for all values of the variable“. This is a way to distinguish identities from equations that are to be solved for specific values. Not all textbooks use it, but it is a good practice.
Problem 1: Aim toward the goal
Doctor Rick replied, using the first example to illustrate how he thinks:
Thanks. I’d like to walk through one problem at a time with you. Let’s start with the separate image:
Show that -1 + cos α 1 + cos α ------------- + ------------- ≡ 2(1 + tan α) sec α + tan α sec α - tan αThe first thing I would choose to do here is to carry out the addition of fractions on the left. This looks like a really good first step because I can see what will happen with the common denominator: it will be a difference of squares. Do you see that? It’s very possible that we’ll be able to apply a “Pythagorean identity” to that denominator.
Give that a try, and show me your work as far as you can take it.
Here we have a step that is both conventional, and supported by a look ahead. Sarah showed how one attempt got her tangled up:
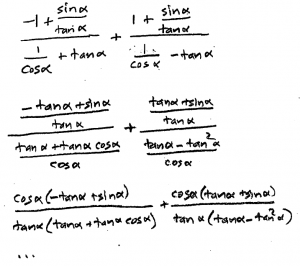
I’ve worked out all of the ones l sent already, but only with some help here and there, once l realised what was the first step, the rest followed easily. I’m attaching one of my original attempts. I’m ending up taking a much longer way which sometimes ends up leading to nowhere. I usually used to manage something like this, but when l don’t manage all the ones l try, I’m finding it off-putting instead of fun.
Doctor Rick wrote back, again focusing on the thinking:
Hi, Sarah. Proving trig identities is a lot like solving puzzles. As you know, they can be a lot of fun when you succeed, but really tedious when we can’t find our way through them. I like to do Sudoku, but now and then there is a supposedly easy puzzle that I get stuck on. If I put the puzzle aside for later, I may then find one thing I’d missed, and everything comes together after that. Since Sudoku are just puzzles, I can just skip one if it gets boring. We ought to be able to do that with trig identities, too; it’s OK not to solve them all. We all have a “blind spot” now and then.
But you’d like to get better at this. Looking at your work, I wonder why you tried replacing cos α by (sin α)/(tan α). Did you have some other identity in which this actually helped? It isn’t something I’d think of. As Doctor Rob said in the Archive answer I showed you, a good first step (when you don’t know what else to do) is to replace all tan, cot, sec, and csc with expressions using only sin and cos. Then you only need to consider the identities involving sin and cos — that’s simpler to think about. Introducing tan when it wasn’t there, doesn’t make things simpler.
If you had done what I’m suggesting (which, of course, is different from what I suggested last time), you’d have:
-1 + cos α 1 + cos α sin α ------------- + ------------- ≡ 2(1 + ----- ) 1 sin α 1 sin α cos α ----- + ----- ----- - ----- cos α cos α cos α cos αThis certainly doesn’t look simpler yet, but the fact that we only have sin and cos should help soon. Now there’s something I see to do next: multiply the numerator and denominator of each fraction on the left by cos α. Why? Because this will make the expression simpler, by getting rid of the “fractions within fractions”.
Now, eventually I’m going to come back around to my earlier suggestion: carrying out the addition of fractions (common denominator and all that). Asking myself why I’d do this, I’d say that it’s because I don’t know any (basic, memorable) identities involving a sum of fractions. I’m aiming to make things look more like what I know. As with putting the expression in terms of sin and cos, I’m trying to increase my chance of recognizing a pattern I can use.
Does this help at all? We can keep discussing your thinking on various problems and see what we discover. Let me just say this (which you probably already know, at least in theory): One of the most overlooked steps in problem-solving is the last — to look over your work to see what lessons you can learn from it. Did you see a pattern that turned out to be useful? Or, looking back with the benefit of hindsight, do you see something you could have done that would have gotten you to the goal more quickly? When I asked myself and you why we did certain things above, it was with the idea of abstracting some possibly useful principles for future problems.
The key idea here is that we are trying to make an expression (a) simpler, (b) more familiar, and (c) more like the other side. Each of these short-term goals makes it likely we will be able to move forward.
After some discussion, he demonstrated both methods for this problem, which I’ll include here. The first, which Sarah said worked better for her, started with combining the fractions:
Here’s my work with the first method:
-1 + cos α 1 + cos α ------------- + ------------- sec α + tan α sec α - tan α (-1 + cos α)(sec α - tan α) + (1 + cos α)(sec α + tan α) ≡ -------------------------------------------------------- (sec α + tan α)(sec α - tan α) -sec α + tan α + cos α sec α - cos α tan α + sec α + tan α + cos α sec α + cos α tan α ≡ ---------------------------------------------------------- sec2 α - tan2 α 2 tan α + 2 ≡ --------------- 1 ≡ 2(1 + tan α)I did more than one thing at a time on some steps to condense the proof somewhat. This method depends on knowing the identity
sec2 x - tan2 x = 1and a few other identities involving more than just sin and cos. For those who can’t see these things so readily, converting to sin and cos can make the steps easier to see, though it does take longer.
The second method, as mentioned, is a good fallback when you don’t see what else to do, as it allows you to use the more familiar identities, even though it may get more complicated:
Here is the rest of the sin-and-cos-first method. I hadn’t tried following that method through to the end, but I will now:
To show that -1 + cos α 1 + cos α ------------- + ------------- ≡ 2(1 + tan α) : sec α + tan α sec α - tan α -1 + cos α 1 + cos α LHS ≡ ------------- + ------------- 1 sin α 1 sin α ----- + ----- ----- - ----- cos α cos α cos α cos α cos α (-1 + cos α) cos α (1 + cos α) ≡ ------------------ + ----------------- 1 + sin α 1 - sin α (-1 + cos α)(1 - sin α) + (1 + cos α)(1 + sin α) ≡ cos α ------------------------------------------------ (1 + sin α)(1 - sin α) (-1 + cos α + sin α - sin α cos α + 1 + sin α + cos α + sin α cos α) ≡ cos α ----------------------------------- 1 - sin2 α 2(sin α + cos α) ≡ cos α ---------------- cos2 α 2 (sin α + cos α) ≡ ----------------- cos α ≡ 2(tan α + 1) ≡ 2(1 + tan α), RHS of identity to be proved.
Back in the original discussion, Sarah responded:
l don’t know why l changed cos to sin/tan, but l probably said if you can change tan to sin/cos then it works that way too. l now realise it makes it much longer.
Also, you substituted on both the left and right hand side. I was told that you can’t do that, because you need to start working on one side, and get to the other, or first work on one side and reach a dead end, do the same on the other side, and have both dead ends equal.
I’ve tried a couple of others and l seem to be getting the hang of it slowly.
Doctor Rob’s article is helpful.
I think l should practice easy ones to get the technique and confidence, then move to harder ones, seeing them as a challenge.
If you want to discuss some others, and we can both show our methods, l’m open to that – we can both analyse after the different methods (if they’re different)
Problem 6 (a,b): Train your intuition
Doctor Rick answered her question, then suggested the next problems to try:
Working on both sides is something we have discussed in Ask Dr. Math, and Dr. Peterson looked at some of these discussions in our Blog:
Different Ways to Prove a Trigonometric Identity
(The first thing he looks at is Dr. Rob’s general method that I showed you earlier. Then he gets into your question about whether we have to start at one end and go through to the other.)
For practice, let’s look at the four-part Question 6 that you showed me earlier. I consider part (a) to be much simpler than the one we’ve been discussing. Part (b) is also relatively easy.
(a) (cos x + sin x)(cos x – sin x) ≡ 1 – 2 sin2 x
(b) sin2 x – sin4 x ≡ cos2 x – cos4 x
What did you do with these identities? Did you notice any patterns or things to try right away? What happened when you tried them? The first thing that occurs to me in each case works out well, but it may be that my intuition has been trained by lots of practice so that I see things that you don’t notice yet – or I don’t even notice things that you do, that don’t work out. Our goal, at least in part, is to train your intuition to focus on truly useful things.
A teacher may consider some things “obvious” that a student can’t yet see at all; and may totally miss the distracting obstacles the student needs to avoid. This is why we want to see it through the student’s eyes in order to help!
Sarah showed her work for each problem:
l tried these two again; this time, intuition worked both times and am attaching my method.
Doctor Rick commented on the thinking behind each solution:
Regarding the first problem,
(cos x + sin x)(cos x - sin x) ≡ 1 - 2 sin2 xyou have done well. I see that you multiplied out the left side and then canceled the “cross terms”. Were you able to see, without doing that all out, that you’d get a difference of squares? If you can see this ahead of time, it can help you recognize that multiplying out the product is definitely a simplifying step. I’d probably multiply out anyway in this situation, but getting a glimpse of what’s coming next is part of the skill set that makes proving identities easier.
On my part, I also recognize that the difference of squares that you get, cos2 x – sin2 x, is the double-angle identity — it’s cos(2x). This isn’t useful in proving the identity, but I also know that 1 – 2sin2 x (or something like that — I may not remember it exactly) is an alternate form of that identity. Thus I saw something coming — namely, that this proof will be something I’ve seen before, when the alternate form was proved. The more you’ve seen before, the easier it is to recognize useful patterns.
Your method on the second problem is not what I did, but I can see that you used a good technique. I’m supposing that you noticed that the right-hand side of the identity to be proved had only cosines, so you chose to rewrite the left-hand side in terms of cosines as well. That’s good thinking, using the form of the “target” expression to guide you in choosing your steps.
Here’s my method. I worked on both sides at once in my exploration. Where one side is distinctly simpler than the other, it’s good to start work on the more complicated side, on the theory that it will be easier to recognize when you’re heading toward the simpler expression. In this problem, though, both sides are equally complicated. So I began like this, factoring on both sides:
sin2 x - sin4 x cos2 x - cos4 x siin2 x (1 - sin2 x) cos2 x (1 - cos2 x) sin2 x (cos2 x) ≡ cos2 x (sin2 x)Now I had identically equal expressions on both sides, so I could rework my exploration into a standard-style proof. This is the idea of “building the bridge from both sides toward the middle, then crossing the bridge from one side to the other.”
sin2 x - sin4 x ≡ sin2 x (1 - sin2 x) ≡ sin2 x (cos2 x) ≡ (1 - cos2 x)(cos2 x) ≡ cos2 x - cos4 xThis looks a little simpler than your proof, but yours is perfectly good, and it has the advantage that the reader can make a good guess at how you thought it through. “Elegant” proofs (not that mine is particularly elegant) tend to hide the thought process that produced the proof, so that you may think, “I would never have thought of that.” Thus they aren’t so much help in learning to do your own proofs!
What is intuition?
Sarah expanded an earlier thought:
I just realised something from what you said: sometimes the more you know, the more it can interfere and make it harder – how do you know what is useful and what is not? The more you know, the more you need to sift to see what you need and what will actually work!
Also, thank you – especially for getting my interest into this, highlighting the whys, the thought process, explaining things so clearly, the advantages of certain methods and for everything 🙂
Doctor Rick responded:
To tell the truth, as I was writing about “the more you’ve seen before,” I had a contrary thought similar, in a way, to yours: As I get older, I find that more of the people I see remind me of someone I once knew — just because I’ve known a lot of people! That doesn’t do me much good, though; it just confuses me — could this actually be the person I’m reminded of? (If you’ve ever read Agatha Christie’s Miss Marple mystery novels, you’ll recognize that this is how the elderly Miss Marple solved crimes — they reminded her of people and situations she’d known in her little village, and that gave her insight into likely motives. But that’s fiction, and in any case, my mind doesn’t work that way.)
Getting back to math, all I can say is that we develop our intuition by noting what steps have proved useful in the problems we have worked. Yes, the number of things we might do at a given step can grow, but we find that not all of them are equally likely to move us forward in proving an identity. In this way, we develop heuristics such as those listed by Dr. Rob — techniques that are more likely to help solve a problem. We can’t be sure these things will help, but we try them first.
Mentioning heuristics reminds me that another of Dr. Peterson’s blogs examined a discussion I had with a student about a challenging identity proof. You might be interested in this one too:
Sarah added:
A bit of a digression here, but you got me thinking; what would you say mathematical intuition is? And how do you train your intuition (other than by practice)? Do you think it is innate or do you develop it? I personally think it is both, because not everyone can “see” certain things, but l think you can develop and work on what you have.
Doctor Rick answered:
Regarding the nature of intuition, I haven’t studied psychology, I’m just writing as a layman regarding that field. To me, intuition is essentially subconscious pattern-matching — making associations between a current situation and things we’ve experienced before, so as to reach a conclusion without formal logical reasoning. Of course, in mathematical proof, we can’t forget about formal logical reasoning! Rather, we use the intuitive process as an aid in the exploration phase as we search for a line of formal logical reasoning.
Under this understanding, intuition is learned, as it is built up of our experiences. Thus practice is the key to mathematical intuition, or problem-solving skill. But as I have already said, in order for that practice to develop our skill effectively, we need to do that final step in problem-solving: to think about what we have done, looking for lessons to be learned.
A harder one?
Sarah was ready for a challenge:
Do you have a good one for me, which requires some easy stuff, but which may be harder to see please? I’m willing to try out a more challenging one. If you do have one, l’m very ready to try it out. Or any one really, which might teach me the techniques required.
Your part about intuition – very interesting; agreed.
Doctor Rick offered a problem to try:
It’s hard to tell how difficult you might find a particular identity proof problem, just as the difficulty ratings of Sudoku puzzles don’t always match my experience with them. But I have some problems that at least look interesting. Let’s see how you do with this one:
1 Prove that ------------- ≡ sec x – tan x sec x + tan x
Sarah was up to the task:
Thank you for the question.
l managed this one on my own.
I did
LHS = 1/((1/cosx) + sinx/cosx)
= cosx/ (1+sinx)
Then l multiplied by (1-sinx) /(1-sinx)
cosx – cosx sinx / (1-sin^2x) = cosx(1-sinx) / cos^2 x = (1-sinx)/cosx = sec x – tan x
Getting the hang of them now, thanks for the help!
Doctor Rick responded:
Your work is good.
You used the fall-back idea of writing everything in terms of sin and cos. Then, I suppose, you may have recognized the useful pattern that multiplying (1 ± sin x) or (1 ± cos x) by what we might call its trig conjugate (I just made that up) results in a difference of squares to which the basic Pythagorean identity can be applied.
If you were more familiar with the other Pythagorean identities, you could have done the same with fewer steps. (I’ve told you that I don’t have these identities fully memorized myself, I have to derive them in my head to be sure.) Here is what this approach would look like:
1 sec x - tan x sec x - tan x ------------- × ------------- ≡ --------------- sec x + tan x sec x - tan x sec2 x - tan2 x sec x - tan x ≡ ------------- ≡ sec x - tan x 1Again, you did well. Let me also show you how one might approach this as if we were solving an equation – something that I know you have been trained not to do:
1 ------------- = sec x – tan x sec x + tan x 1 = (sec x - tan x)(sec x + tan x) 1 = sec2 x - tan2 xBut this is always true (if necessary, you can do this to verify it:)
1 = 1/cos2 x - sin2 x / cos2 x 1 = (1 - sin2 x)/cos2 x cos2 x = 1 - sin2 xThis you definitely recognize as an identity.
Now, this “solution of the equation” has a clear relationship to my proof of the identity, Rather than multiplying both sides of the equation by (sec x + tan x), we work with the LHS alone, multiplying it by 1 in the form (sec x + tan x)/(sec x + tan x). This is the idea presented in Dr. Peterson’s blog “Different Ways to Prove a Trigonometric Identity“, in the section “Can you work on both sides?”.
This was the end of the discussion. I’m sure the subject will come up again.