(An archive question of the week)
While I’m showing some recent explanations of basic trigonometry techniques, this is a good time to look at an even more basic explanation of the essentials of the subject for a beginner.
Right triangle trigonometry
Here is the question, from 2001:
Trigonometry in a Nutshell I'm in 8th grade in my school and in my math class we're doing stuff about trigonometry (sine cosine hypotenuse). But what is trigonometry? Can you give me some good easy questions in trigonometry so I can try using it? Thanks.
This calls for a non-scary introduction to the subject that will show some of the power of trig, without showing difficult parts. Doctor Ian took up the challenge:
Hi Jimmy, Believe it or not, I just spent part of last weekend explaining trigonometry to my mother, who was upset because about 50 years ago she wanted to become a radio technician in the navy, but ended up as a pharmacist's assistant because she couldn't get the hang of trigonometry. So I'm going to tell you what I told her.
The best things to tell someone who is just being introduced to a subject may be the same things you would tell someone who has struggled with it. An overview of what it’s all about, giving the big picture without getting tangled up in details, can help anyone.
Trigonometry is typically introduced using right triangles, and that’s where Doctor Ian goes:
When you have a right triangle,
/|
/b|
C / |
/ | A
/ |
/_a___|
B
there are basically five things that you can know about it: the lengths of the sides (A, B, and C), and the measures of the acute angles (a and b). The third angle is always 90 degrees because it's a right triangle.
If you know two of the sides, you can use the Pythagorean theorem to find the other side:
A = sqrt(C^2 - B^2)
B = sqrt(C^2 - A^2)
C = sqrt(A^2 + B^2)
And if you know either angle, a or b, you can subtract it from 90 to get the other one:
a + b = 90
Note that his notation is the opposite of what we usually see; he is using upper-case letters for lengths of sides, and lower-case letters for angles. A more typical picture would look like this:
But this is just a common convention, not a mathematical necessity.
The Pythagorean Theorem and the sum of angles allow you to find a missing side from two given sides, or a missing angle from two given angles (one being 90°). Where trigonometry proper is needed is to handle relationships between sides and angles, mixing the two together.
Trigonometric functions (ratios)
But what if you know the sides and you want to know the angles? Or you know an angle and a side and you want to know the other sides?
Well, here is the central insight of trigonometry: If you multiply all the sides of a right triangle by the same number (k), you get a triangle that is a different size, but which has the same angles:
/|
/b|
/ |
/| k*C / | k*A
/b| / |
C / | / | k*A A
/ | A / | --- = -, etc.
/ | / | k*B B
/_a___| /__a_____|
B k*B
Why is that interesting? Well, it means that if you know the _ratio_ of any two sides, it tells you what the angles are.
That is, similar triangles have the same angles, and the same ratios of sides; so the angles determine what the ratios will be, and the ratios determine what the angles will be. But in most cases, it doesn’t actually tell you what they are, until you use trigonometry!
There are some special triangles for which mere geometry is enough. One of these is half of an equilateral triangle:
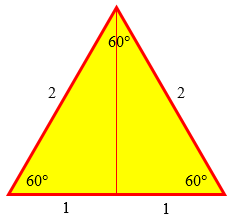
For example, let's look at a right triangle in which the acute angles are 30 and 60 degrees:
/|
/ |
/30|
C / |
/ | A
/ |
/_60___|
B
If side B is 1 unit long, then side C is 2 units long, and side A is
A = sqrt(2^2 - 1^2)
= sqrt(4 - 1)
= sqrt(3)
units long. Now, notice that I haven't said what a 'unit' is. It could be a mile, or an inch, or 13.5 cm, or the distance from my big toe to the base of a bookcase on the other side of the room. If I know that angle a is 60 degrees, then I know that the following must be true:
the ratio of A to C is sqrt(3)/2
the ratio of B to C is 1/2
the ratio of A to B is sqrt(3)/1
And, just as importantly, if I know that for a particular triangle, the ratio of A to B is sqrt(3)/1, then angle a _must_ be 60 degrees. It can't be any other angle.
This illustrates how the angle determines the ratio of sides, and the ratio determines the angle. The sides themselves could be any size, but they must have these ratios.
So, what we can do is write down a table, in which we list all the ratios for all the angles of interest: angle a ratio A/B ------- --------- 0 0 . . <= values for other angles filled in . . 30 sqrt(3)/3 . . . . 45 1/1 . . . . 60 sqrt(3)/1 . . . . Now we can use this table to find the ratio A/B if we know angle a - just find the angle in the column on the left, and read the ratio from the column on the right. Or we can use the same table to find angle a if we know the ratio A/B - just find the ratio in the column on the right, and read the angle from the column on the left.
Most angles don’t have nice ratios like these; they have to be calculated as decimal approximations (using methods most of don’t need to know) and put into tables (or, these days, into calculators) for you to use. But the idea is the same.
And since we see that the value of any of these ratios is the same for any triangle with a given angle, each ratio is a function of the angle.
All that’s lacking is names for these functions:
But instead of 'ratio A/B for angle (a)', we use the shorter name 'tangent of angle a', or just 'tan(a)'.
Since there are three possibilities for which pair of sides you might know - A and C, B and C, A and B - we have three different functions:
angle a => sin(a) = A/C
cos(a) = B/C
tan(a) = A/B
So we can make up a table that looks like this:
Machinery Handbook Math Pages: Trig Tables
http://www.industrialpress.com/ext/staticpages/handbook/trigpages
A sample of the table (whose link I have updated from the original):
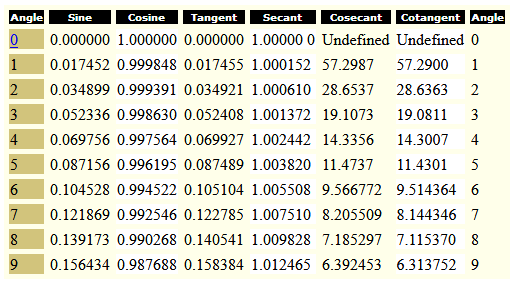
Before calculators (and even now, in places where calculators are not commonly available), much more detailed tables were needed. Here is an example of such a table for the sine.
By the way, the names, “sine”, “cosine”, and “tangent”, along with “secant”, “cosecant”, and “cotangent”, can be considered as arbitrary names that just have to be memorized. Here are one page from Ask Dr. Math about the names, and another about memorizing their meanings:
Latin Origins of Trig Functions Explaining How SohCahToa Works
I’ve seen many other mnemonics for them.
Note that we don't really need include the sec, csc, and cot functions, since we can just compute them from the sin and cos functions: sec(a) = 1 / cos(a) csc(a) = 1 / sin(a) cot(a) = cos(a) / sin(a)
The first three functions listed (sine, cosine, and tangent) cover all three pairs of sides; the last three are their reciprocals, so that we have a name for every possible ratio of two sides (in either order). That’s overkill, but can be useful sometimes to make a formula simpler.
Solving a right triangle: examples
Now Doctor Ian moves on to how these functions can be used to solve a triangle (that is, find all the missing parts when you know two):
So, having said all that, the whole _point_ of trigonometry is this: If you have a right triangle in which you know one side and any other side or angle, you can figure out the remaining sides and angles without having to measure them. In fact, here are all the possibilities:
You know How you find the others
------------- -----------------------------------
two sides Use the Pythagorean theorem to
find the remaining side.
Use the ratios of the sides to
find the angles.
one side and Use the sin, cos, and tan functions
one angle to find the remaining sides.
The other angle is just 90 minus
the one you know.
It’s good to have a few examples, not just a dry, general rule:
That's it. The rest of it is shortcuts and tricks. For example, if you have a triangle like
/|
/ |
C / |
/ |
/ | A
/ |
/_17___|
25
it must be true that
A / 25 = tan(17) 25 / C = cos(17)
A = 25 tan(17) 25 / cos(17) = C
25 * (1 / cos(17)) = C
25 sec(17) = C
where 'sec' is short for 'secant', and sec(x) is the just another way to write 1/cos(x). Anyway, when you've put in about a thousand hours of practice, you will be able to just label the triangle immediately:
/|
/ |
25 sec(17) / |
/ |
/ | 25 tan(17)
/ |
/_17___|
25
Using the table or a calculator, we would find that the vertical side is $$25\tan(17°) \approx (25)(0.3057) \approx 7.64,$$ and the hypotenuse is $$\frac{25}{\cos(17°)} \approx \frac{25}{0.9563} \approx 26.14.$$
Note, by the way, that the picture shows only relationships, and is not at all to scale; we don’t need that. But if we drew it accurately, we would see that because 17° is a small angle, the vertical side is much less than 25, just as we found; whereas the hypotenuse is always longer than either side, in this case just a little longer:
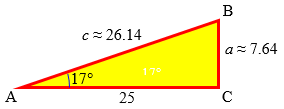
Also, you will be able to use formulas (called 'identities') like
sin(x-y) = sin(x)cos(y) - cos(x)sin(y)
to do tricks like this:
sin(15) = sin(45 - 30)
= sin(45)cos(30) - cos(45)sin(30)
= (1/sqrt(2))(sqrt(3)/2) - (1/sqrt(2))(1/2)
= sqrt(3)/[2 sqrt(2)] - 1/[2 sqrt(2)]
= [sqrt(3) - 1] / sqrt(2)
Whether being able to do these things from memory instead of from a book is _worth_ a thousand hours of your life isn't clear. You'll have to take that up with your state legislature or the Department of Education.
This is just a taste of the more complex things included in trig. When needed, you can look up these things, like the values of the trig ratios, in a table, though many are very much worth knowing, at least as long as you are going to be working actively with them.
Applications
How about a taste of what trig can be used for? Jimmy asked for some easy sample problems. Many important applications can’t be understood until later math courses, but there are many that are easy to appreciate.
Anyway, that's trigonometry in a nutshell. All you have to do to make up problems is draw a right triangle:
/|
/b|
/ |
C / | A
/ |
/ |
/_a____|
B
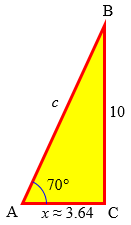
and then make up a story to go with it, in which you know two sides, or a side and an angle. For example, a ladder is leaning against a wall at an angle of 70 degrees with the ground. It just touches the bottom of a window 10 feet off the ground. How long is the ladder? How far from the wall is the bottom of the ladder?
window
/|
/ |
/ |
ladder/ | 10 feet
/ |
/ |
/_70___|
?
Answer: The tangent of 70° is the ratio of the opposite side (10) to the unknown adjacent side, so $$\frac{10}{x} = \tan(70°)$$ $$x = \frac{10}{\tan(70°)} = \frac{10}{2.747} \approx 3.64\text{ feet}$$
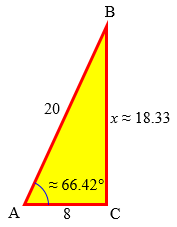
To turn it into a different problem, just change what you know:
window
/|
/ |
/ |
20 ft / | ?
/ |
/ |
/_?____|
8 ft
Answer: First, use the Pythagorean Theorem to find the height: $$8^2 + x^2 = 20^2$$ $$x = \sqrt{20^2 – 8^2} = \sqrt{336} \approx 18.33\text{ feet}$$
The cosine of the unknown angle is the ratio of the adjacent side (8) to the hypotenuse (20), so $$\cos(A) = \frac{8}{20}$$ $$A = \cos^{-1}\left(\frac{8}{20}\right) = \cos^{-1}(0.4) \approx 66.42°$$
Here we used the inverse cosine function, which just means reading the table backward, finding the angle that has a desired tangent.
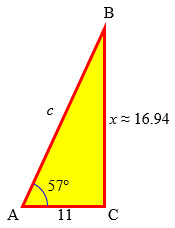
Or, if you get bored with ladders and windows, make up a different story, e.g., a bird is sitting on a flagpole, and the sun is at an elevation of 57 degrees. The shadow of the bird is 11 feet from the base of the flagpole. How tall is the flagpole?
bird
/|
/ |
/ |
/ | ?
/ |
/ |
/_57___|
11 ft
Answer: The tangent of 57° is the ratio of the unknown opposite side (x) to the adjacent side (11), so $$\frac{x}{11} = \tan(57°)$$ $$x = 11\tan(57°) \approx (11)(1.540) \approx 16.94\text{ feet}$$
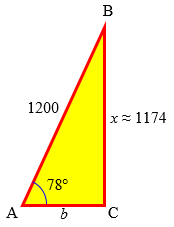
Or one person is at the top of the Grand Canyon, and another is at the bottom. They use a laser range finder to determine that they are 1200 meters apart, and the one below has to look up at an angle of 78 degrees to see the one above. How deep is the canyon?
Answer: The sine of 78° is the ratio of the unknown opposite side (x) to the hypotenuse (1200), so $$\frac{x}{1200} = \sin(78°)$$ $$x = 1200\sin(78°) \approx (1200)(0.9781) \approx 1174\text{ feet}$$
Some people need extra help seeing how to decide which function to use to solve a triangle; here is general explanation of that process:
Sine, Co-sine, and Tangent: SOHCAHTOA
Doctor Ian concluded:
Making up your own problems will give you a much better feel for why this is so useful, and with any luck, you'll start to see why some people even think it's fun. So that's how you make up problems. You solve problems made up by other people by reversing the steps. That is, you read the problem and try to figure out what is at the vertex of each triangle. Then you try to figure out which sides and/or angles you've been given, and which one you're supposed to find. Then you use the Pythagorean theorem and the sin, cos, and tan functions to find it.
Jimmy slightly overstated his response:
Thanks! You really helped me and saved me some money from buying books about trigonometry. This always was a toughy for me on tests, but I think I can work it out next time. Thanks again!
No, this doesn’t take the place of textbooks! But it does make the subject more approachable.
Trig functions, circles, and waves
The day before, another student had asked a similar question, which was combined into this page:
I am totally confused about sine, cosine, and tangent. What are they and where do they come from? All I have been taught is when to use them and where the button is on the calculator. I have tried finding a beginners' guide or tutorial on the net but everything is too advanced. They even use sine etc. with circles and waves, where I thought it was just to do with triangles. Please could you explain them? I think it would be very useful to have explanations on your site, as everybody in my class can use them but nobody knows what they really are.
This time, Michael is familiar with the right triangle trigonometry that was covered above, but wonders about the bigger picture.
Doctor Ian answered this as well, connecting the trigonometric functions first with circles, and then with their graphs:
Hi Michael,
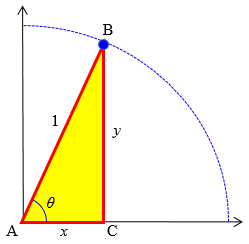
What does trigonometry have to do with circles? Well, draw a circle whose center is at the origin of the x-y plane, and whose radius is 1. Now choose any point on the circle, draw a line segment from the center, and mark the angle a between the positive x-axis and the line segment. You should have something that looks like this:
1|.
| .(x,y)
| / .
| /
| / .
| /
| / .
| / a
---------------
1
Guess what? The coordinates of the point you chose are
(x,y) = (cos(a), sin(a))
Furthermore, since the radius of the circle is 1, the Pythagorean theorem tells us that
(sin(x))^2 + (cos(x))^2 = 1
Actually, a lot of formulas, like the ones you can find in the Ask Dr. Math FAQ: Trigonometry Formulas,
http://mathforum.org/dr.math/faq/formulas/faq.trig.html
are easiest to understand if you think about the unit circle rather than triangles of arbitrary size.
To see clearly why the sine and cosine show up here, we can add a line to make a right triangle:
And what does this have to do with waves? If you start taking different values of a, and plot the corresponding values of x and y (that is, if you plot x and y as functions of a, the way you would normally plot y as a function of x), you get something like this:
x x
| x x x = cos(a)
| x x
+------x-----------x------------
| x x
| x x
x
a=0 90 180 270 360
| y
| y y y = sin(a)
|y y
y-----------y-----------y------
| y y
| y y
| y
a=0 90 180 270 360
Each plot keeps wiggling back and forth between 1 and -1, repeating itself every 360 degrees, which is another way of saying that if you move 360 degrees around a circle, you end up where you started. Anyway, this shape is what is normally thought of as a 'wave'. Lots of things in nature can be understood in terms of waves, so much so that even though the history of the sin and cos functions is mostly about triangles, the major uses of the functions today have to do with describing waves.
Here we’ve started extending the concept of sine and cosine, by allowing our point to go all around the circle rather than staying in the first quadrant where x and y are positive. This is the beginning of an amazing journey through trigonometry, where many new applications open up beyond solving right triangles.
For a deeper answer to Michael’s question, “What are they,” see my post What Are Trig Functions, Really?
