(A new question of the week)
This week and next I will look at a recent discussion on trigonometry that dug deep into two different issues: solving equations, and proving identities. These are good summaries of how to approach these common kinds of problems. This week: solving basic trig equations.
Questions about trig functions
Here is the initial question, from our friend Sarah in June:
Hi,
I’m learning how to solve trigonometric equations, using the CAST rule, but l’m finding it hard.
First of all, is cos(θ) and cos(-θ) the same for all angles? If yes, why? I asked my teacher and he said not necessarily. He also said sin(-θ) is not always -sin(θ) .
Now, when it comes to solving equations, for example, if sin x = -1/2, I would find the sine inverse of 1/2 and draw that in the cosine and tangent quadrant since sin x has to be negative.
However, when they get more complicated, l get stuck. Could you show me an example worked out please, and then give me one to try myself?
Thanks
There are several questions here, but they focus on two things: how signs of trig functions are to be handled, and then how to solve simple equations.
Sines and signs
Doctor Fenton took the question, giving a thorough survey of these topics. He began with the teacher’s statements, which are wrong if they are quoted correctly:
Hi Sarah,
Thanks for writing to the Math Doctors. I don’t know why your teacher said that, but in fact, for any angle θ, cos(θ) = cos(-θ), and sin(-θ) = -sin(θ). (If you are familiar with the ideas of even and odd functions, this says that the cosine function is an even function and the sine function is an odd function.)
To see why, look at how the sine and cosine are defined in terms of the unit circle: see
https://en.wikipedia.org/wiki/Trigonometric_functions
and
https://en.wikipedia.org/wiki/Sine#Unit_circle_definition
The measure of an angle θ in standard position is positive when measured counterclockwise, and negative when measured clockwise. Given an angle θ, find the point (a,b) where the terminal ray of the angle intersects the unit circle. Then cos(θ) = a and sin(θ) = b. If the angle θ intersects the circle at (a,b), then the angle -θ will have its terminal ray intersect the circle at (a,-b).
An even function is one that behaves like an even power (e.g. \(f(x) = x^2\)), in the sense that changing the sign of the input doesn’t change the sign of the output; the graph is symmetrical about the y-axis. In general, for an even function, \(f(-x) = f(x)\). This is true of the cosine and its reciprocal, the secant.
In the same way, an odd function is one that behaves like an odd power (e.g. \(f(x) = x^3\)), in the sense that changing the sign of the input does change the sign of the output; the graph is symmetrical about the origin. In general, for an odd function, \(f(-x) = -f(x)\). This is true of the sine, tangent, cosecant, and cotangent.
In both cases, this is always true – for all x. My best guess is that the teacher might have said that neither of these is true for all functions.
Here is a picture of the unit circle Doctor Fenton refers to:
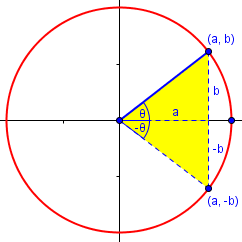
Clearly, the sines of θ and -θ are opposite, while the cosines are the same.
Now, what does CAST refer to? Students in different places are taught different mnemonics or other terminology, but Sarah’s use of it made it (eventually) clear:
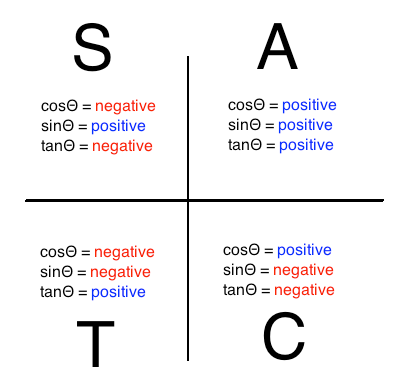
At first, I didn’t understand what you meant by the CAST system, but I think it must refer to the method of determining the sign of the trigonometric functions in each quadrant, starting in the fourth quadrant (lower right) and proceeding counterclockwise: Cosine, All, Sine, Tangent. I haven’t seen that method used before, since all the books I am familiar with use the acronym ASTC (with the mnemonic All Students Take Calculus). If that is correct, your acronym is simpler, but you have to remember to start in the fourth quadrant rather than the first.
You don’t indicate whether you use radians or degrees, but since you seem to be just learning the subject, I will use degrees. However, if you continue to study mathematics, you will need to learn radians.
Here is a picture of the “CAST System” (or Rule, or Method), which is indeed identical to ASTC:
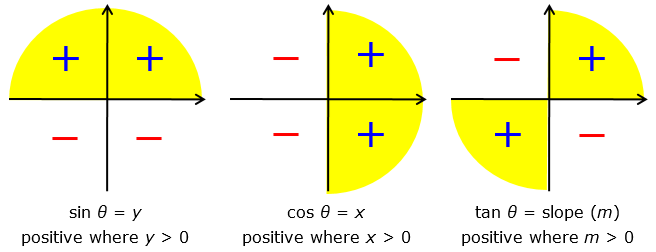
Like the evenness/oddness of trig functions, I prefer to determine the signs from the definition, rather than from the mnemonic (which is derived from the definition). So I just think of these pictures:
Memorizing special angles
When you are solving an equation of the form sin x = y, first you should know that the equation has solutions only if -1 ≤ y ≤ 1. So if y < -1 or y > 1, there are no solutions, and nothing to be done. Students are generally expected to know the values of the trigonometric functions for the “special angles” 0°, 30°, 45°, 60°, and 90°. An easy way to remember these values is to make a table which I call the “half-square root” table. For sine and cosine, write the following table:
θ 0° 30° 45° 60° 90° -------------------------------------------------------------- sin θ [√( )]/2 [√( )]/2 [√( )]/2 [√( )]/2 [√( )]/2 cos θ [√( )]/2 [√( )]/2 [√( )]/2 [√( )]/2 [√( )]/2Next, fill in the following values:
θ 0° 30° 45° 60° 90° -------------------------------------------------------------- sin θ [√(0)]/2 [√(1)]/2 [√(2)]/2 [√(3)]/2 [√(4)]/2 cos θ [√(4)]/2 [√(3)]/2 [√(2)]/2 [√(1)]/2 [√(0)]/2When you simplify the expressions, it becomes:
θ 0° 30° 45° 60° 90° -------------------------------------------------------------- sin θ 0 1/2 [√(2)]/2 [√(3)]/2 1 cos θ 1 [√(3)]/2 [√(2)]/2 1/2 0
When you are asked to solve an equation “exactly”, the solutions will usually be related to these. When you are asked for a decimal answer, you will use the inverse trig functions on your calculator, which determine the angle for which the function has the given value. For instance, if you are told that \(\sin(x) = 1/2\), then you can just recognize that \(x = 30°\). But if you are told that \(\sin(x) = 0.3\), then you have to calculate \(x = \sin^{-1}(0.3) \approx 17.46°\).
Solving a simple equation
All solutions in an interval
When solving trigonometric equations such as sin x = -1/2, the instructions often say either “find all solutions”, or “find all solutions x such that 0° ≤ x < 360°.
In this second case, for any number c such that -1 < c < 1, there are exactly two solutions x in the interval 0° ≤ x < 360° for the equations
sin x = c and cos x = c.
For your example, sin x = -1/2, you know from CAST that the two solutions are in the third and fourth quadrants. From the table, you know that sin 30° = 1/2, so sin(-30°) = -1/2 , and x = -30° is one solution. However, it is not in the given interval.
The two solutions (for sine and cosine, respectively) look like this when the sign is positive:
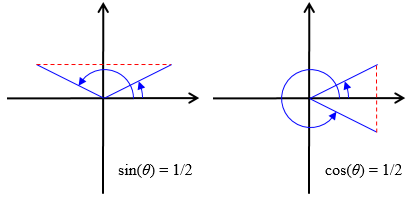
The two angles with the same positive sine are supplementary (θ and 180° – θ), with θ in the first quadrant. The two angles with the same positive cosine would have been θ and –θ, but to make them positive, the latter has to be described as 360° – θ. We’ll see how this is handled below.
In our example, the sine is negative. Here are the two solutions for negative sine or cosine:
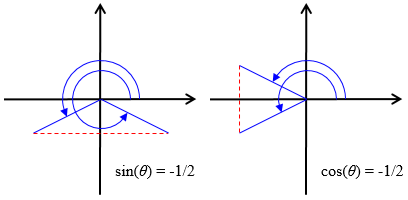
Here, as Doctor Fenton said, our first thought for the sine case would be –θ, where θ would have a positive sine; we need several tools to be developed below. The first is this:
The other most important feature of the trigonometric functions is that they are periodic, which means that their values repeat at regular intervals. For sine and cosine, that interval is 360°, so that sin(-30°) = sin(-30°+360°) = -1/2. That is, sin(330°) = -1/2 , and x = 330° is one of the solutions.
This is where my 360° – θ for the cosine case above came from. Rather than use the negative angle –θ, we add 360° to it to make it positive:
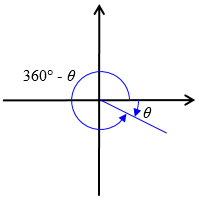
Reference angles
The easiest way to get the other solutions is to use a “reference angle”. For any angle θ, the reference angle of θ is the smallest angle to the x-axis. For a first quadrant angle such as 30°, if you go clockwise from 30°, it is 30° back to the positive x-axis, but to go counterclockwise, you must go 150° to reach the negative x-axis, so the reference angle of 30° (or any other first quadrant angle) is 30°. For a second quadrant angle such at 120°, to reach the positive x-axis, you must go 120° clockwise, but to reach the negative x-axis, you only need to go 60 degrees, so 60° is the reference angle of 120°.
The reference angle is always a first quadrant angle.
If θ is an angle, θ’ is its reference angle, and T is any trigonometric function, then T(θ)=±T(θ’), and you choose the sign using the CAST rule.
The reference angles for θ in each of the quadrants are as shown here:
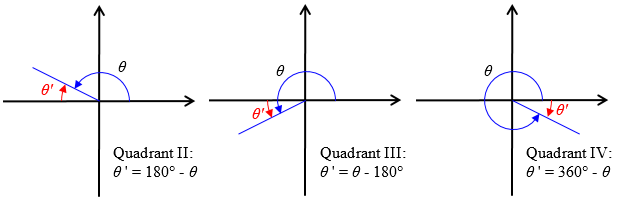
To finish the problem, since you know that -30° (or 330°) is one solution, the reference angle for this solution is 30°. The other solution must be in the third quadrant, and have the same reference angle. In the third quadrant, 180° ≤ x ≤ 270°, so the smallest angle will always be clockwise back to the negative x-axis. The third quadrant solution must be 30° more than 180°, or 210°. The two solutions are 210° and 330°.
Briefly, we solve \(\sin(\theta) = -\frac{1}{2}\) by seeing that the reference angle will be 30° because \(\sin(30°) = \frac{1}{2}\); and in order to get a negative sine, we want angles in the third and fourth quadrants. These are 30° more than 180° and 30° less than 360°, and therefore are 210° and 330°.
General solution (all of them)
That was the way to find the two solutions of this equation in the interval 0° ≤ x < 360°. The problem could be asking for more:
If the problem wants you to find all the solutions, you can find them from these two solutions by adding or subtracting 360° to each of the two angles:
x = 210° + k*360°, where k is any integer, or x = 330° + k*360° for any integer k.
All solutions are coterminal with one of the two we found, so we just add any integer times 360°. Written out, these solutions are \(\dots, -410°, -150°, 210°, 570°, \dots\) (going both ways from our first angle), and\(\dots, -390°, -30°, 330°, 690°, \dots\).
One more time:
For another example, to solve cos x = [√(2)]/2, we see from the special angles table that x=45° is one solution. The reference angle for the other solution is 45°, so you know from CAST that the other angle is in the fourth quadrant, with a reference angle of 45°, so the other solution in the interval 0° ≤ x< 360° is 315° (or -45°).
Does this help? If you have any questions, please write back and I will try to explain further.
Here we are solving \(\cos(\theta) = \frac{\sqrt{2}}{2}\), and our solution in the first cycle is {45°, 315°}; the general solution is {45° + k 360°, 315° + k 360° for any integer k}.
Follow-up questions
That was Doctor Fenton’s answer to the initial question. Sarah had some follow-up questions:
Thanks so much for your detailed reply, it’s very helpful.
A few follow-up questions, please:
- Could you elaborate a bit more on the periodicity part please? And what would it be for tangent?
- I didn’t get the k part, what do you mean any integer k?
- We would usually present -30° and 330° as two separate answers; should they be presented as one?
Also, we do use radians, and we do have some trig identities too.
To work with radians, you’d essentially just replace 360° everywhere with 2π.
We’ll look at subsequent questions on identities next week.
Periodic functions
Doctor Fenton answered the three main questions.
First question: Could you elaborate a bit more on the periodicity part please? And what would it be for tangent?
An angle is formed by two rays emanating from a common point (the vertex of the angle). In “standard position”, one ray (the initial ray or initial side) is from the origin, along the positive x-axis, and the other ray can be thought of as obtained by rotating a second ray from the origin, starting along the positive x-axis, through a given angle θ, to become the terminal ray or side of the angle. As this moving ray rotates, it crosses the unit circle at a point with coordinates (x,y). cos θ is defined to be the x-coordinate of the intersection point, and sin θ is defined to be the y-coordinate.
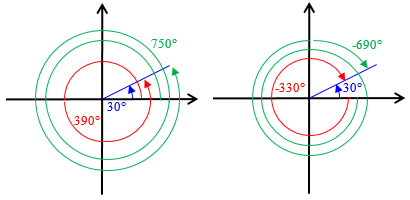
As the terminal keeps rotating, it eventually makes a complete revolution and then points along the positive x-axis again, and this happens when θ reaches 360°. As the terminal ray continues to rotate, the intersection point after it has rotated by an angle θ beyond one complete revolution will be the same point where it intersected the circle after rotating by angle θ. That is the cause of the periodicity, and why that period is 360°. Rotating the terminal ray by 390° leaves the terminal ray in the same position as rotating by 30°. Rotating one more full revolution adds another 360° to the angle, making 750°, and so on. The sine and cosine of an angle repeat after every additional 360° rotation, in either direction, clockwise or counterclockwise.
So these angles (30°, 390°, 750°, and also -330°, -690°, and many others) all have the same sine and cosine, because the terminal ray is the same for all of them:
On the other hand, the period of the tangent function is only 180°, half the period of the sine and cosine. Why? Because the tangent is the slope of the ray, \(\frac{y}{x}\), and rays 180° apart have the same slope. So as soon as you have rotated 180° beyond a given angle, the tangent repeats:
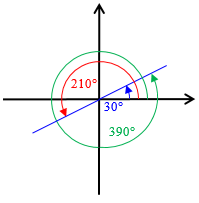
The tangents of 30°, 210°, and 390° are all the same, namely \(\frac{\sqrt{3}}{3}\).
General solution details
Second question: I didn’t get the k part; what do you mean any integer k?
If you only look at the position of the terminal ray, you can’t tell how many complete revolutions it made, so sin θ will have the same value for θ, θ+360°, θ+360°+360°= θ+2*360°, θ+3*360°, θ+4*360°, and so on, as long as the number of complete rotations is a whole number.
The complete revolutions could also have been made clockwise, so sin θ will have the same value for the angles θ, θ-360°, θ-2*360°, θ-3*360°, θ-4*360°, and so on. All these angles have the same form: θ+k*360°, where k is an integer (a positive or negative whole number).
So the angles listed and shown above correspond to k = 0, 1, 2 in the first picture, and k = 0, -1, -2 in the second.
How to state the solution
Third question:We would usually present -30° and 330° as two separate answers; should they be presented as one?
These are still different angles: one is obtained by a clockwise rotation of 30° and the other by a counterclockwise rotation of 330°. However, their terminal rays are in the same position. Angles like these are called “coterminal” because their terminal rays are in the same position. All the angles above, θ+k*360°, where k is an integer, are coterminal.
If a problem asks for ALL solutions of a trigonometric equation, you find the solutions in the fundamental period, and then write the formulas for all the angles coterminal to these angles.
For the tangent function, the fundamental period is 180° instead of 360°, so for any angle θ, tan θ = tan (θ+k*180°) for any integer k. The same is true for the cotangent function.
Next week we’ll look at Sarah’s question about identities.

Pingback: Three Trigonometric Inequalities – The Math Doctors
Pingback: Trigonometric Equations: Finding All Solutions – The Math Doctors