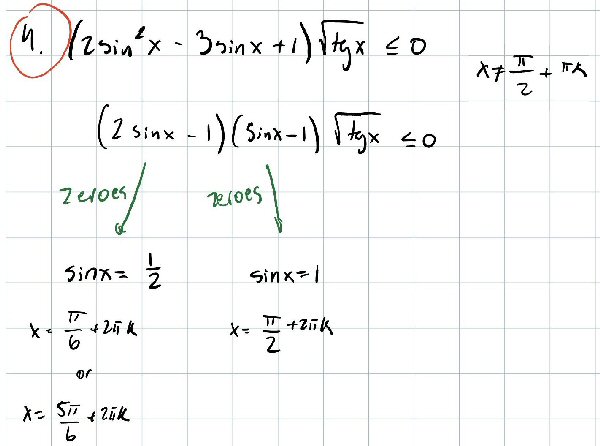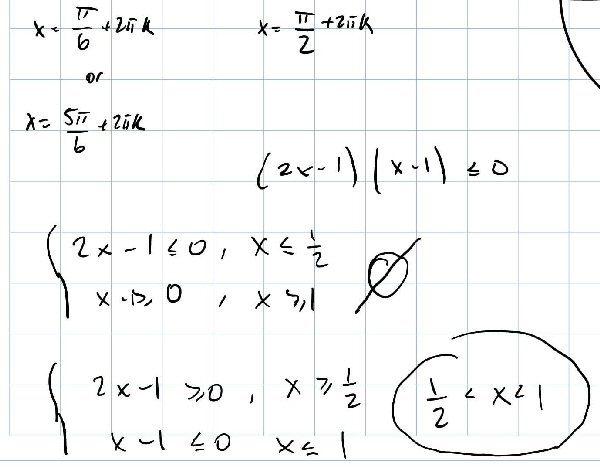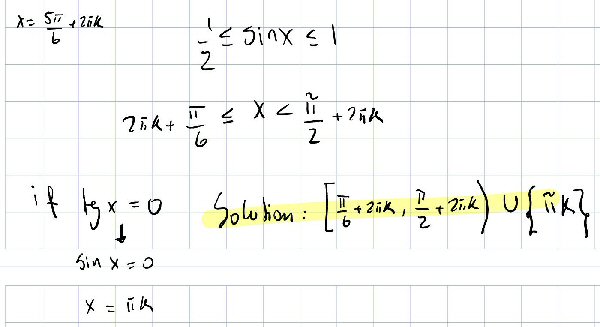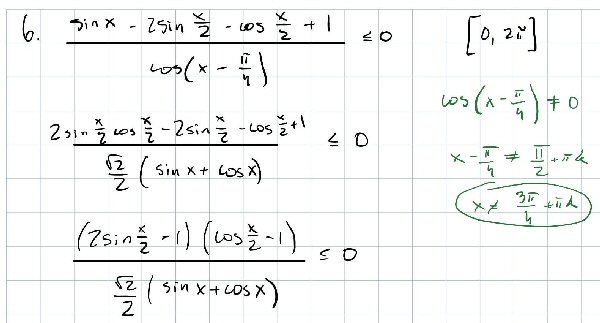Three Trigonometric Inequalities

(A new question of the week)

We often solve basic trigonometric equations; but a recent set of questions dealt with challenging trigonometric inequalities, which bring with them a new set of issues. We’ll look at several of those here, which combine trig with polynomials, rational functions, and more. Each will illustrate something new to watch for.

First problem: a rational inequality

All of these came, over several days in late October, from Amal. Here is the first:

I need to find the values of x that satisfy this inequality within the range [π, 2π], and this is what I’ve got. Not sure if what I’ve done until now is correct, but I don’t know how to continue from this point on.

 

We need to solve $$\frac{\sin(2x)+2\cos^2(x)-1}{\cos(x)-\cos(3x)+\sin(3x)-\sin(x)}\le2\cos(x)$$ for \(\pi\le x\le2\pi\). (We’ll see that the handwritten interval is wrong, and this is what was intended; that is not important.)

Amal has applied a multiple-angle identity, $$\cos(2x)=2\cos^2(x)-1,$$ to the numerator, and two sum-to-product identities, $$\cos(a)-\cos(b)=-2\sin\left(\frac{a+b}{2}\right)\sin\left(\frac{a-b}{2}\right)\\\sin(a)-\sin(b)=2\cos\left(\frac{a+b}{2}\right)\sin\left(\frac{a-b}{2}\right),$$ to the denominator, then factored and canceled to get $$\frac{1}{2\sin(x)}\le2\cos(x),$$ then correctly found values that lead to equality. But this is an inequality!

Doctor Rick answered:

Hi, Amal.

I believe you have correctly found the four solutions of the associated equation in [0, 2π]. There is a little more work to do in order to solve the inequality.

When you multiply through by 2 sin x, you need to consider the sign of that quantity: if it is negative, then the direction of the inequality must be reversed (replace ≤ by ≥).

In each case, I would then decide where the inequality is true by sketching the graph of sin(2x) along with the line y = 1/2. You have found the points where the line intersects the sine curve; where, in relation to these, is the sine curve above the line?

There are several possible approaches to an inequality like this; Doctor Rick is suggesting minimal changes to what Amal has done, which is our usual practice. (I’ll show an alternative method at the end.) This will require considering separate cases to correctly handle the multiplication by the denominator. (There’s at least one other issue he hasn’t yet touched upon.)

Amal replied:

I believe I have made a mistake. The range in which the solutions should be is [π, 2π].

Does that change anything?

On the other hand, I completely ignored the possibility of 2sinx being negative, as you mentioned. My question is now, how do I combine both solutions for when ½ ≤ sin2x and ½ ≥ sin2x?

Doctor Rick answered:

You write:

I believe I have made a mistake. The range in which the solutions should be is [π, 2π]. Does that change anything?

Do you mean that what was written on the paper was incorrect, and you are only interested in the solutions in the interval [π, 2π]? That’s fine, just keep it in mind in what follows.

On the other hand, I completely ignored the possibility of 2sinx being negative, as you mentioned. My question is now, how do I combine both solutions for when ½ ≤ sin2x and ½ ≥ sin2x?

Don’t worry about combining solutions until you have the solutions.

Under what conditions is 2 sin x < 0? What inequality do you get when 2 sin x < 0, and what do you find for its solution set? (You’ve already got the inequality to solve when 2 sin x > 0.)

Amal said,

Ok now looking at it, since the range is [π, 2π], the inequality has to be 1/2 ≥ sin2x, given that if one plugs any value from the range into 2sinx, it will give a negative value.

Doctor Rick acknowledged:

Good, that’s what I wanted you to see — and it’s why I held off on discussing combining of solutions: we really have only one inequality to consider.

So can you proceed with solving the inequality

1/2 ≥ sin(2x), π ≤ x ≤ 2π

using the sketching method I suggested, or any other method?

If a different interval had been required, we would actually have to follow through on both cases!

Let’s review is what he has done so far:

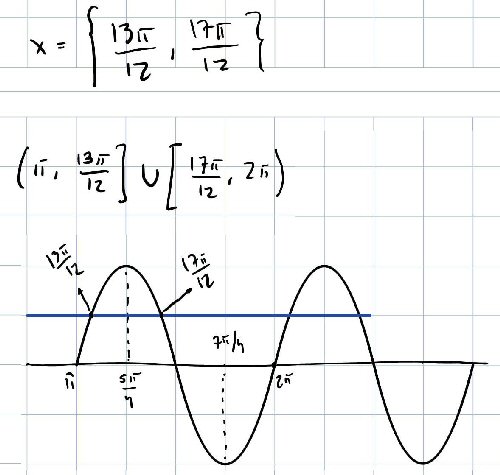
Given $$\frac{\sin(2x)+2\cos^2(x)-1}{\cos(x)-\cos(3x)+\sin(3x)-\sin(x)}\le2\cos(x)$$ for \(\pi\le x\le2\pi\), he obtained $$\frac{\sin(2x)+\cos(2x)}{2\sin(2x)\sin(x)+2\cos(2x)\sin(x)}\le2\cos(x)$$ as before, and factored and canceled to get $$\frac{\sin(2x)+\cos(2x)}{2\sin(x)(\sin(2x)+\cos(2x))}\le2\cos(x)\\\frac{1}{2\sin(x)}\le2\cos(x).$$ Then, knowing that since \(\pi\le x\le2\pi\), \(\sin(x)\le0\), so that he could multiply both sides by that, reversing the direction, to obtain $$1\ge4\sin(x)\cos(x),$$ which is equivalent to $$\sin(2x)\le\frac{1}{2}.$$ Equality holds for $$2x=\frac{\pi}{6}+2k\pi\text{ or }\frac{5\pi}{6}+2k\pi\\x=\frac{\pi}{12}+k\pi\text{ or }\frac{5\pi}{12}+k\pi$$ and for \(\pi\le x\le2\pi\), this yields $$x=\frac{13\pi}{12}\text{ or }\frac{17\pi}{12}.$$ This is where he had stopped originally.

Now we’re ready to move beyond that.

Solving a simple inequality graphically

Amal responded:

Here’s the sketch I made, and above it the solution.

Now I do have one last question. The solution for this exercise should be (π, 13π/12] ∪ [17π/12, 15π/8) ∪ (15π/8, 2π), according to answer sheet. Where could have I missed that 15π/8?

Looking at a sketch of the graph over \([\pi,2\pi]\), we see that the inequality holds for values of x that are not between them.

But there’s more! What cancellation does

Doctor Rick answered,

That looks good! Now, what have we both missed?

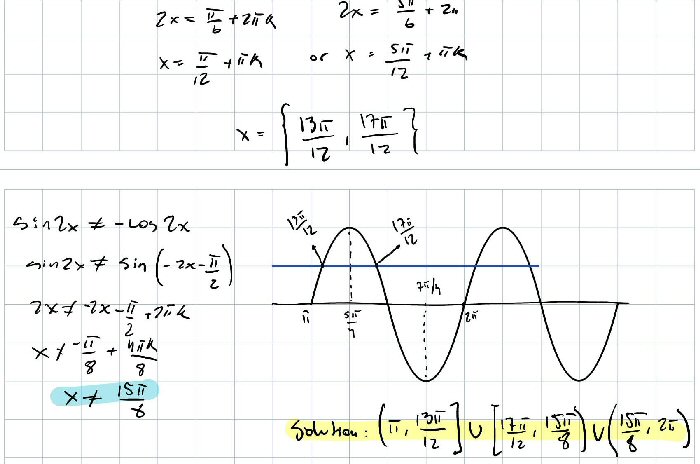
One thing we always need to be careful about is losing (or gaining) roots when we simplify an equation. You canceled (sin 2x + cos 2x) from the numerator and denominator in the equation. What if that quantity equals zero – could that cause problems?

When (sin 2x + cos 2x) equals zero, the numerator on the LHS is 0, and the denominator is 0. If we were solving an equation, I would thus think: OK, it’s not an issue, because any value of x that makes that quantity zero won’t be a solution anyway; the LHS is not a number. And that’s how I did think — forgetting that this is an inequality! It does matter that any such value of x is not in the solution set.

So now you know what else you need to do.

So, if the problem had been to solve $$\frac{\sin(2x)+2\cos^2(x)-1}{\cos(x)-\cos(3x)+\sin(3x)-\sin(x)}=2\cos(x),$$ the cancellation $$\require{cancel}\frac{\cancel{\sin(2x)+\cos(2x)}}{2\sin(x)\cancel{(\sin(2x)+\cos(2x))}}=2\cos(x)$$ would be innocuous, because the expression being canceled is not zero for the solution values we found. But in the inequality, the solution is an interval that includes a value we have to exclude.

Amal was now ready to answer the problem:

Ok perfect. So what I added to my solution is sin2x ≠ -cos2x, therefore the only value of x within the range that cannot be a solution is 15π/8.

So we have to exclude \(\frac{15\pi}{8}\) from the solution set because $$\sin(2x)+\cos(2x)=\sin\left(\frac{15\pi}{4}\right)+\cos\left(\frac{15\pi}{4}\right)=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}=0and the PHS would be 0/0.$$

Doctor Rick approved:

Good! I was confident that you wouldn’t need more help on this. You now have some ideas that might help with your other problems if any remain unsolved.

I solved sin 2x + cos 2x = 0 in a different way, rewriting it as tan 2x = –1. Either way works.

This approach gives $$\sin(2x)+\cos(2x)=0\\\frac{\sin(2x)}{\cos(2x)}+\frac{\cos(2x)}{\cos(2x)}=0\\\tan(2x)=-1\\2x=\frac{3\pi}{4}+k\pi\\x=\frac{3\pi}{8}+\frac{k\pi}{2}$$ and the solutions in our interval are \(\frac{11\pi}{8}\) or \(\frac{15\pi}{8}\). The former is already excluded.

We’ll return to this problem at the end, with both a different approach, and a full solution.

Second problem: A polynomial and radical inequality

The second problem was submitted immediately after that last one:

Don’t know what else to do besides what I’ve written. Also, the square root of tangent of x confuses me a bit and don’t know what to do with it.

Note that, as is common in some parts of the world, he uses the notation \(\text{tg}(x)\) where I would use \(\tan(x)\), for the tangent. We generally stick with the notation a student uses.

It’s also worth noticing that this time we want the general solution, not just a solution restricted to a particular interval.

Here, as before, he has done nicely in finding zeroes; this time the complicating issue, beyond finding intervals, is not cancelling a factor, but that odd square root. What do we do with that?

I answered (while the first question was still being discussed):

Hi, Amal.

You have correctly found where the LHS is zero, apart from the influence of the tangent. The latter has an effect only when the tangent is 0, as otherwise √tg(x) is a positive number, and you can safely divide both sides by it. But in addition, it affects the domain of the entire inequality, so it will eliminate some parts of the solution you’d find otherwise.

There are three separate issues: the factor \(\sqrt{\text{tg}(x)}\)  is never negative, so it won’t affect the sign of the product, which is what matters in an inequality like this; but its zeros will be solutions, and it will also prevent some otherwise-solutions from being accepted, because they would not be in the domain of the left-hand side.

But so far, he has only found zeroes of the other part, and has not dealt with the inequality.

Now you need to think about the inequality aspect, which you can treat the same way as any polynomial inequality. Can you show me how you would solve (2x – 1)(x – 1) ≤ 0? You can use the same technique here to obtain an inequality in sin(x), and solve that.

So, either just show me how you solve the polynomial inequality, or try applying that idea to the sine, and we can discuss whatever you show me.

A polynomial inequality like \((2x-1)(x-1)\le0\) can be solved by recognizing that the LHS can only change sign at its zeroes, and either testing the value in each of the intervals between, or by considering the sign of each factor individually. Or, as Amal will do below, it can be solved by considering separate cases: Since the product has to be negative, either the first factor is negative and the second positive, or vice versa.

Amal complied:

This is how I solved the inequality, but idk how to apply it to the actual inequality.

(I meant to write the solution as ½ ≤ x ≤ 1.)

Yet another way you could solve this would be to recognize that the LHS is a parabola opening upward, so it will be negative between its two zeroes.

However we do it, we have found, replacing \(x\) there with \(\sin(x)\), that \(\frac{1}{2}\le \sin(x)\le1\).

 I responded:

Good.

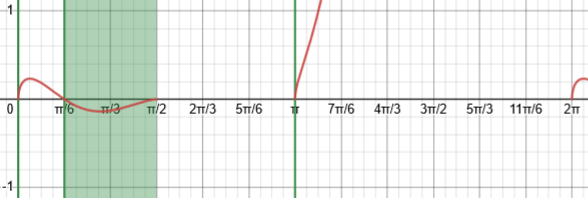
I would next sketch a graph of the sine, over the domain implied by the radical. What is that domain?

At the end you’ll want to consider what happens when tan(x) = 0, which adds something to the answer.

Here is the graph of the sine, including the interval into which it must fall, and the resulting interval in x (shaded):

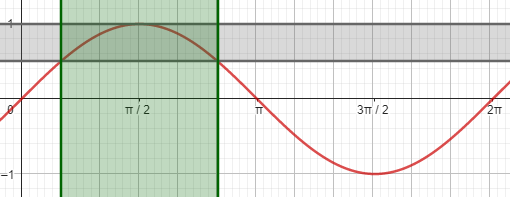
But we still need to deal with \(\sqrt{\text{tg}(x)}\).

Amal finished the solution:

Ok so, I applied ½ ≤ x ≤ 1 to sinx, there for if we solve for x, it should be 2πk + π/6 ≤ x ≤ π/2 + 2πk, but since the “domain” you asked about (which I should’ve referred to it as a restriction) says that x cannot be π/2 + πk (because of tanx), the expression should be 2πk + π/6 ≤ x < π/2 + 2πk.

Then if we consider what happens when tanx is 0, we get that x should be πk, so I add it to the solution.

In my own usage, a “restriction” would be a statement in the problem itself restricting the solution to some interval, as in the first problem; here the “restriction” is implied by the domain of the functions involved. But the terminology is not important.

Here is my version of the work: \(\frac{1}{2}\le \sin(x)\le1\) is true for \(\left[\frac{\pi}{6},\frac{5\pi}{6}\right]\) (repeating every period), but the factor \(\sqrt{\text{tg}(x)}\) on one hand adds in the solution \(x=k\pi\) because the factor is 0 there, and on the other hand restricts the solution to \(0\le x<\frac{\pi}{2}\), where the tangent exists and is not negative, so that the actual solution is the intersection of what we previously found and the shaded regions shown here:

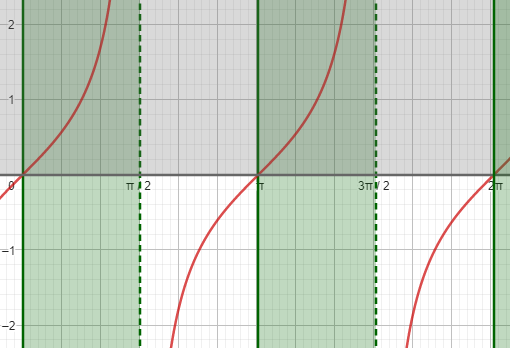
Combining these, we get his answer, which in one period, \([0,2\pi)\), is \(\{0\}\cup\left[\frac{\pi}{6},\frac{\pi}{2}\right)\cup\{\pi\}\).

I concluded:

That looks good. I graphed the LHS and marked (in green) the region in which it is ≤0, and it agrees with what we both found:

I would say that the fact that tan(x) can be zero adds 0, π, …, but the domain of the radical requires that tan(x) ≥ 0, which is why the solution stops at π/2, while the domain of the tangent function eliminates π/2.

These are not easy problems!

Amal closed:

Makes total sense! And yes, definitely not easy ones.

Thank you for your help.

Third problem: a bigger rational inequality

Amal sent a third problem while the second was being discussed:

This is as much as I can simplify the inequality, but don’t know how to continue.

Also in green is the values of x that will not satisfy the expression.

This must be solved for [0, 2π]

This is closer than the first was to a traditional rational inequality, with sinusoids replacing the variable, and he has done a good job putting it into factored form. He first wisely put the numerator in terms of functions of the same angle (using the double-angle formula \(\sin(2\theta)=2\sin(\theta)\cos(\theta)\)), and then found it could be factored (by grouping). He also rewrote the denominator using an angle-sum identity, which turns out to be unnecessary but was not a bad idea. He also found the values of x that make the denominator zero, which must be excluded.

I answered:

Hi, Amal.

You’ve done just what I did to start, except that I’m not sure that the change to the denominator helps.

Now that you have it in factored form, I would identify where each of the two factors on top, and the factor on the bottom, is zero, and note where it changes sign.

Then I would do as I do for rational inequalities, and mark the sign of each factor in these regions on a number line, then find which regions yield a negative or zero (and defined) value for the entire expression. We show a similar method toward the bottom of this article:

A Rational Inequality with Huge Exponents

Amal responded:

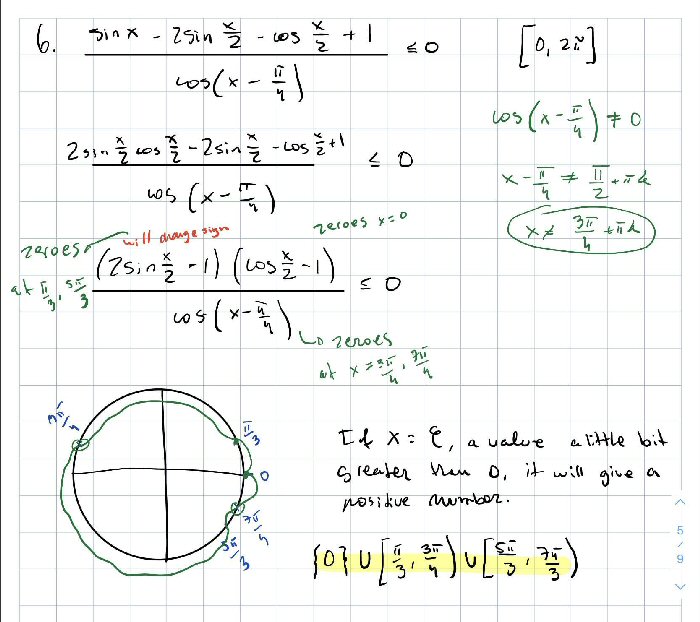
Perfect, I thought of doing something like that but I wasn’t sure when it would change signs.

Here’s my work.

He has reverted the denominator to its original form, and then determined the intervals over which each factor would be positive, negative, or zero. His interesting graph is a circular version of the number line I had suggested, with the green line outside for positive and inside for negative; this works nicely considering the periodic nature of the functions. Here is my version (using a straight line), filling in some details:

• A, \(\displaystyle2\sin\left(\frac{x}{2}\right)-1\) is positive when \(\displaystyle\sin\left(\frac{x}{2}\right)>\frac{1}{2}\), which is when \(\displaystyle\frac{\pi}{6}<\frac{x}{2}<\frac{5\pi}{6}\), so that \(\displaystyle\frac{\pi}{3}<x<\frac{5\pi}{3}\). Thus, it is \(\le0\) in \(\displaystyle\left[\frac{\pi}{3},\frac{5\pi}{3}\right]\).
• B, \(\displaystyle\cos\left(\frac{x}{2}\right)-1\) is positive when \(\displaystyle\cos\left(\frac{x}{2}\right)>1\); that is, it is never positive, but is zero at \(x=0\). 
• C, \(\displaystyle\cos\left(x-\frac{\pi}{4}\right)\) is positive when \(\displaystyle\cos\left(x-\frac{\pi}{4}\right)>0\), which is when \(\displaystyle-\frac{\pi}{2}<x-\frac{\pi}{4}<\frac{\pi}{2}\) so that \(\displaystyle-\frac{\pi}{4}<x<\frac{3\pi}{4}\). Thus, it is negative in \(\displaystyle\left(\frac{3\pi}{4},\frac{7\pi}{4}\right)\); when it is zero, the expression is undefined.

Putting these together on a number line, we can mark up regions where each of the three factors is positive (green), zero (blue), and negative (red), and then mark where the entire LHS is negative or zero, and not undefined (because the denominator is zero, white):

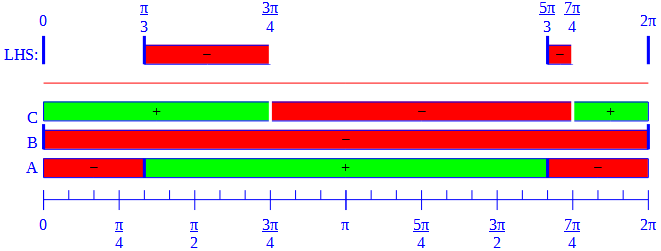
$$\{0\}\cup\left[\frac{\pi}{3},\frac{3\pi}{4}\right)\cup\left[\frac{5\pi}{3},\frac{7\pi}{4}\right)$$

(Note that he accidentally wrote \(\frac{7\pi}{3}\) instead of \(\frac{7\pi}{4}\), which I never noticed until now.)

The quick method, described in the post I referred to, is to mark the locations where any factor is zero (marking whether it makes the LHS zero or undefined); then mark the sign of the LHS, by changing it at each point where it should; and then graph the solution set by including each point and interval as appropriate:

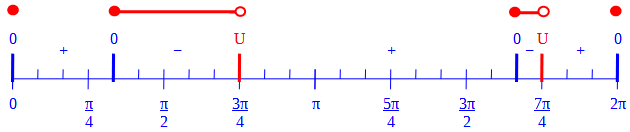
I concluded, summarizing what I just did:

Yes, that agrees with my work.

I found that the first factor on top changes sign at π/3 and 5π/3, being positive in the middle; the second factor is always negative, except for being 0 at x=0; and the denominator changes sign at 3π/4 and 7π/4, at which points the fraction is undefined, being negative in the middle. Putting it together, I got the same answer you show.

There were more similar problems to come, but these had the most interesting discussions.

Solving the first problem as a rational inequality

I’d like to try solving the first problem in a style similar to what we did in the last one. Given a rational inequality (in trig functions), like our $$\frac{\sin(2x)+2\cos^2(x)-1}{\cos(x)-\cos(3x)+\sin(3x)-\sin(x)}\le2\cos(x)$$ it is standard to first get a zero on the right-hand side and simplify as one big fraction on the left. After Amal’s simplifications (but omitting the cancellation), we have this: $$\frac{\sin(2x)+\cos(2x)}{2\sin(x)(\sin(2x)+\cos(2x))}\le2\cos(x)\\\frac{\sin(2x)+\cos(2x)}{2\sin(x)(\sin(2x)+\cos(2x))}-2\cos(x)\le0\\\frac{\sin(2x)+\cos(2x)}{2\sin(x)(\sin(2x)+\cos(2x))}-\frac{4\sin(x)\cos(x)(\sin(2x)+\cos(2x))}{2\sin(x)(\sin(2x)+\cos(2x))}\le0\\\frac{\sin(2x)+\cos(2x)-2\sin(2x)(\sin(2x)+\cos(2x))}{2\sin(x)(\sin(2x)+\cos(2x))}\le0\\\frac{(1-2\sin(2x))(\sin(2x)+\cos(2x))}{2\sin(x)(\sin(2x)+\cos(2x))}\le0$$

We can cancel \(\sin(2x)+\cos(2x)\), keeping in mind that points where this is zero (namely \(x=\frac{3\pi}{8}+\frac{k\pi}{2}\)) will be excluded; now we have $$\frac{1-2\sin(2x)}{2\sin(x)}\le0$$ The numerator is zero (and changes sign) at \(x=\frac{\pi}{12}+k\pi,\frac{5\pi}{12}+k\pi\), and the denominator for \(x=k\pi\). The sign is positive just above \(x=0\), so it is negative or zero in \(\left[\frac{\pi}{12}+2k\pi,\frac{5\pi}{12}+2k\pi\right]\), and in \(\left(\pi+2k\pi,\frac{13\pi}{12}+2k\pi\right]\), and in \(\left[\frac{17\pi}{12}+2k\pi,2k\pi\right)\).

Here is the number line model:

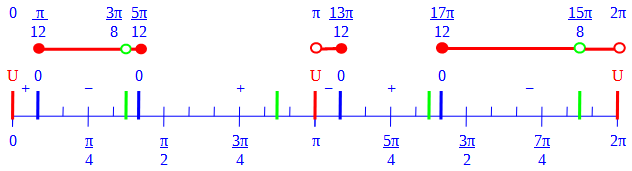
Here, the green marks correspond to the cancellation, which doesn’t change the sign but makes a hole in the solution set.

In the original problem, we considered only \(\pi\le x\le2\pi\); here we see the full solution for each period (that is, you can add \(+2k\pi\) to each number): $$\left[\frac{\pi}{12},\frac{3\pi}{8}\right)\cup\left(\frac{3\pi}{8},\frac{5\pi}{12}\right]\cup\left(\pi,\frac{13\pi}{12}\right]\cup\left[\frac{17\pi}{12},\frac{15\pi}{8}\right)\cup\left(\frac{15\pi}{8},2\pi\right)$$

Here is a graph of the LHS (red) and RHS (green), with shading showing where red is below green:

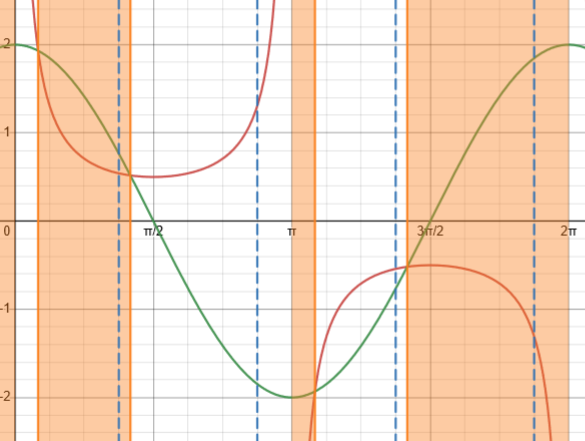
The broken lines indicate the values that must be omitted because of the canceled factor; neither Desmos (which I used for this) nor GeoGebra (which couldn’t do the shading) can show the required holes.