When a challenging type of problem is written with unexpectedly large numbers, it can look impossible. Today’s discussion illustrates how to get past the hurdles.
The problem
The problem came from Arsh in April:
Q) [x((x+5)^2016)((x-3)^2017)((6-x) ^1231)]/((x-2)^10000)((x+1)^2015)((4-x)^242) ≥ 0
Since our site doesn’t yet allow LaTeX formatting, and Arsh chose not to insert the problem as a picture as some do, this was hard to read. Doctor Rick did the best he could to restate it more readably, and to ask for further information:
Hi, Arsh. Could you say more? I am not sure what the question is — are you requested to prove the inequality, or to determine whether it is true or false?
If I am reading it correctly, the inequality is
x(x + 5)2016(x - 3)2017(6 - x)1231 --------------------------------- ≥ 0 (x - 2)10000(x + 1)2015(4 - x)242You might proceed as if you were preparing to sketch a graph of a rational function. Enumerate the x-intercepts and vertical asymptotes of the graph — values of x for which the function is either zero or undefined — and then either consider the behavior in the vicinity of each of these values, or consider the sign of the function in each interval demarcated by these values. If it’s a true-false question, just one such consideration can tell you what you need to know.
It is not uncommon for students to focus on an equation, and forget that the words of a problem are very important! What are we to do with this inequality?
Cross-multiplying by even powers
Arsh replied:
In this question we have to find the values of x which satisfy the inequality.
I have cross multiplied (x-2)^10000 and (4-x)^242 as they will give positive since the power is even. Then I have multiplied (x+1) up and down giving (x+1)^2016 in denominator which will also give positive so I have again cross multiplied (x+1)^2016.
Now the inequality is – x(x+5)^2016 (x-3)^2017 (6-x) ^1231 (x+1) ≥ 0
Now what should I do? I used to do such type of inequality by finding critical points but I can’t get the critical point here.
Here is Arsh’s problem:
$$\frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}}{(x-2)^{10000}(x+1)^{2015}(4-x)^{242}} \ge 0$$
He has multiplied both sides by the even powers in the denominator, which is valid because it will not change the sign:
$$\frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}}{(x-2)^{10000}(x+1)^{2015}(4-x)^{242}}\cdot(x-2)^{10000}(4-x)^{242} \ge 0\cdot(x-2)^{10000}(4-x)^{242}$$
$$\frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}}{(x+1)^{2015}} \ge 0$$
Then he multiplied by \((x+1)\) in the numerator and denominator, to make an even power, then got rid of that the same way:
$$\frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}(x+1)}{(x+1)^{2015}(x+1)} \ge 0$$
$$\frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}(x+1)}{(x+1)^{2016}} \ge 0$$
$$\frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}(x+1)}{(x+1)^{2016}}\cdot(x+1)^{2016} \ge 0\cdot(x+1)^{2016}$$
$$x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}(x+1) \ge 0$$
There are some good ideas here, with a focus on simplifying the problem before actually solving it (though the domain has been changed, so more care is needed).
Doctor Rick responded by giving an additional hint at the direct method he had in mind, while also suggesting how to continue with Arsh’s idea:
I don’t know why I didn’t include “solving the inequality” as one of the possibilities of what the question might be asking. We get more questions about proving inequalities (as identities) than about solving them; I suppose that’s why my mind moved first in that direction (and quickly saw that it wasn’t an identity).
Still, you can use one of the methods I suggested in relation to sketching the graph — specifically, finding the sign in each interval between zeros/asymptotes. I didn’t say how to do that, hoping that you knew the idea. In any given interval, you can determine the sign of each factor. If an even number of terms are negative then the function as a whole is positive; if an odd number of terms are negative, then the function as a whole is negative.
What you have done isn’t necessary, but you can continue in that direction and get rid of all the huge exponents, resulting in a less intimidating function! Going back to the original inequality,
x(x + 5)2016(x - 3)2017(6 - x)1231 --------------------------------- ≥ 0 (x - 2)10000(x + 1)2015(4 - x)242you can divide through by (x + 5)2016 * (x – 3)2016 * (6 – x)1230, because these are all non-negative because of the even exponents. Likewise, multiply through by (x – 2)10000 * (x + 1)2016 * (4 – x)242, which is again non-negative.
Now there will be five intervals of x to consider, separated by the four zeros. In which of these is the product positive? (Don’t forget, in addition, to check all the zeros of the original function, because they will satisfy the “equal to zero” part of the inequality.)
We’ll get back to the direct method soon.
For now, let’s carry out this full simplification, starting from the original and taking the approach of multiplying by an even power of every base, in such a way as to both clear the denominator and avoid changing signs:
$$\frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}}{(x-2)^{10000}(x+1)^{2015}(4-x)^{242}}\cdot\frac{(x-2)^{10000}(x+1)^{2016}(4-x)^{242}}{(x+5)^{2016}(x-3)^{2016}(6-x) ^{1230}} \ge 0$$
$$\frac{x(x-3)^{1}(6-x) ^{1}(x+1)^{1}}{1} \ge 0$$
This leads to what Arsh gives next. But be aware: By eliminating the powers of \((x + 5)\), \((x – 2)\), and \((4 – x)\) entirely, we have lost the fact that x can’t be -5, 2 or 4.
I got x(x-3)(6-x)(x+1)≥0
Now zeroes are 0,3,6,-1 . Since one is negative so the function as a whole is negative.
Plotting on number line I get -(-1,0] U [3,6]
Now, looking at original inequality I get that -5 is also a solution and 4 cannot be a solution.
Therefore, {-5} U (-1,0] U [3,4) U (4,6]
Arsh has wisely gone back to the problem and caught the zeros that were lost; but one thing he said seems wrong, probably just because it was stated too briefly.
Reducing in place by even powers
Doctor Rick made a couple clarifications, before suggesting an alternate method:
I agree with your final answer. However, I wonder if you meant what you said at the start: “Now the zeroes are 3, 6, 0, -1. Since one is negative so the function as a whole is negative.” These words suggest a misunderstanding of my suggestions: it isn’t the number of negative zeroes that matters, but the number of negative factors in the expression when x is in each interval between zeroes (or vertical asymptotes — poles — of the rational function). Yet somehow you got the correct answer in the end, so I imagine either you misstated what you did, or you used some other method to get your result.
I suspect (after looking at this several times) that what Arsh actually meant was that one of the factors, \((6-x)\), has a negative leading coefficient, so that for large x it will be negative, and the whole expression is negative on the rightmost interval – or something like that!
Doctor Rick continued:
It would probably be safer to retain the structure of the original function as we reduce the powers — keep all factors, with even or odd exponent as required, and keep the factors where they were initially, in the numerator or denominator. Thus we could simplify to
x(x + 5)2(x - 3)(6 - x) ----------------------- ≥ 0 (x - 2)2(x + 1)(4 - x)2The zeroes and poles (“critical points” as I believe you called them), in numerical order, are:
-5, -1, 0, 2, 3, 4, 6
Thus you need to consider each of the following intervals (ignoring the points themselves for now):
(-∞, -5)
(-5, -1)
(-1, 0)
(0, 2)
(2, 3)
(3, 4)
(4, 6)
(6, ∞)
Determine the sign of the function within each interval, then consider whether the function is zero or undefined at each critical point in order to complete the work.
You said you used to solve such inequalities by finding critical points (but you were having trouble finding those points for some reason). Therefore perhaps you have no problem now; after all, you did get the correct answer. (Perhaps you used a different method, such as considering whether the sign changes at each critical point — that can be faster.) If there is anything else you’re wondering about, though, let me know.
That was the end of the discussion, since Arsh understood everything well. For the sake of other readers, I’ll expand on this a little.
First, if you are not familiar with rational inequalities, the following pages may offer some helpful background:
Rational Inequality Solving a Rational Inequality Solving Rational, Radical, and Polynomial Inequalities
(I’ll wait while you read at least the first of those, if you need to.)
Solving without simplifying
Now consider our inequality, in the original form:
$$\frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}}{(x-2)^{10000}(x+1)^{2015}(4-x)^{242}} \ge 0$$
We are looking for regions on the number line where the LHS (left-hand side) is either positive or zero. It can only change signs where one of the factors in either the numerator or the denominator is zero; when the numerator is zero, the inequality is true, and then the denominator is zero, the LHS is undefined, so the inequality is false. Therefore, we can put closed dots on a number line (representing values that are part of the solution) at x = 0, -5, 3, and 6; and open dots (representing values that are not part of the solution) at x = 2, -1, and 4:
![]()
Now, each of the factors with an even power will always be positive (except where it is zero, which we have covered), so we can now ignore it. The factors with odd powers will change sign at the dots corresponding to each of them; so the shortcut Doctor Rick mentioned is to first find the sign when x is far to the right, like this:
$$\frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}}{(x-2)^{10000}(x+1)^{2015}(4-x)^{242}} = \frac{(+)(+)^{2016}(+)^{2017}(-) ^{1231}}{(+)^{10000}(+)^{2015}(-)^{242}} = \frac{(+)(+)(+)(-) }{(+)(+)(+)} = \frac{-}{+} = -$$
So we can mark the sign as negative at the right, and then work to the left, changing the sign at each of the odd factors, namely -1, 0, 3, and 6:

The same can be determined (more slowly, but perhaps more safely) by repeating what we did above for each interval separately, listing the sign of each factor, and so finding the sign of the entire expression.
Now, we mark the intervals on which the sign is positive; then the dots and segments together constitute the solution of the inequality:

And there is the solution Arsh got before: $$\{-5\}\cup(-1, 0]\cup[3, 4)\cup(4, 6]$$
At the start it was mentioned that this could be obtained by taking some of the steps required for graphing the function $$y = \frac{x(x+5)^{2016}(x-3)^{2017}(6-x) ^{1231}}{(x-2)^{10000}(x+1)^{2015}(4-x)^{242}}.$$ Here is the graph of the simplified version Doctor Rick suggested,
$$y = \frac{x(x+5)^{2}(x-3)(6-x) }{(x-2)^{2}(x+1)(4-x)^{2}}$$
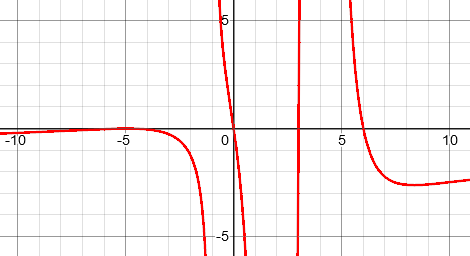
(The graph of the original function is impossible to draw, because the numbers rise far too fast.) The solution is the set of values of x where the graph is at or above the axis.
The graph just touches the axis at \(\{-5\}\); it is above the axis in \((-1, 0]\cup[3, 4)\cup(4, 6]\), with -1 and 4 excluded because it is not defined at those asymptotes. The scale of this graph makes it hard to see the asymptotes.
