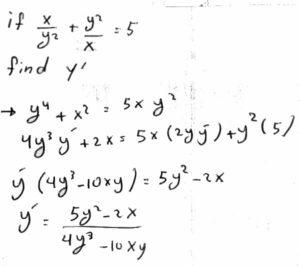(A new question of the week)
Having just discussed the Chain Rule and the Product and Quotient Rules, a recent question about implicit differentiation (which we covered in depth two years ago) fits in nicely. This raises an important issue: when you get an apparently wrong answer, you may just have done something wise that caused your (correct) answer to differ from the book’s! We’ll also look at a three-year-old question as a further illustration of how these work.
My answer doesn’t match the book’s!
This question came from Amia in mid-December:
Hi doctors,
I’m trying to solve the question attached:
I had a different answer than the answer in the book which is y/2x.
I can’t simplify my answer to be the same as the book.
Is there any mistake in my solution?
In implicit differentiation, we are given an equation that implicitly defines a function (or several functions), and differentiate both sides of the function with respect to x, using the chain rule; then we solve for the desired derivative, \(\frac{dy}{dx}\).
What he has done is first to clear fractions by multiplying both sides by \(xy^2\), $$\frac{x}{y^2}+\frac{y^2}{x}=5\\\frac{x}{y^2}xy^2+\frac{y^2}{x}xy^2=5xy^2\\x^2+y^4=5xy^2$$
This simplifies the equation considerably, eliminating the need for the quotient rule. But we’ll see that it also complicates things …
Then he differentiated each term, using the power rule, $$\left(x^2\right)’=2x,$$ and the chain rule, $$\left(y^4\right)’=4y^3y’,$$ and the product rule, $$\left(5x\cdot y^2\right)’=\left(5x\right)’\left(y^2\right)+5x\left(y^2\right)’\\=5y^2+5x\left(2yy’\right)=5y^2+10xyy’.$$
Then he collected terms containing \(y’\), factored, and divided: $$2x+4y^3y’=5y^2+10xyy’\\4y^3y’-10xyy’=5y^2-2x\\(4y^3-10xy)y’=5y^2-2x\\y’=\frac{5y^2-2x}{4y^3-10xy}.$$
We could try to simplify by factoring, but it clearly isn’t equivalent to the book’s answer: $$y’=\frac{5y^2-2x}{4y^3-10xy}=\frac{5y^2-2x}{2y(2y^2-5x)}.$$
1: Do it the book’s way
I answered:
Hi, Amia.
This is not unusual. When I help a student with implicit differentiation, I generally tell them to do that and nothing else; any simplification you make before differentiating will change the result so it will not look like the book’s answer — even though what you do is an obviously good thing to so.
So answer #1 is, just differentiate as given, and you will get their answer.
We saw the same phenomenon in A Surprising Route to a Differential Equation, where (under Alternative 4) I said
Implicit differentiation can result in very different looking formulas when you process the problem differently before differentiating. This is because the implicit derivative by nature doesn’t explicitly take into account the fact that x and y are related; if we were to solve for y and plug that into the different expressions we get for the derivative, to get a formula in terms of x (rather than both x and y), we would find that they agree. [This is a danger in assigning implicit differentiation problems, because anything special that you do before differentiating, no matter how wise, may result in your answer being different from what the teacher expects!]
Clearing fractions is a typical good-idea-gone-wrong that I see students make; it is “wrong” only in that it will give different results than a teacher expects, not necessarily that those results are always more complicated or less useful than what we get directly.
So let’s differentiate the equation as given:
$$\frac{x}{y^2}+\frac{y^2}{x}=5$$
Combining into a single fraction, $$\frac{x^2+y^4}{xy^2}=5$$
By the quotient rule (and all the other rules!), $$\frac{\left(2x+4y^3y’\right)\left(xy^2\right)-\left(x^2+y^4\right)\left(y^2+x\left(2yy’\right)\right)}{\left(xy^2\right)^2}=0\\\frac{\left(2x^2y^2+4xy^5y’\right)-\left(x^2y^2+2x^3yy’+y^6+2xy^5y’\right)}{x^2y^4}=0\\\frac{x^2y^2-2x^3yy’-y^6+2xy^5y’}{x^2y^4}=0$$
Solving for \(y’\), $$x^2y^2-2x^3yy’-y^6+2xy^5y’=0\\x^2y^2-y^6=(2x^3y-2xy^5)y’\\y’=\frac{x^2y^2-y^6}{2x^3y-2xy^5}=\frac{y^2(x^2-y^4)}{2xy(x^2-y^4)}=\frac{y^2}{2xy}=\frac{y}{2x}$$
And that’s the book’s answer.
2: Try to get from our answer to the book’s
Answer #2 is, your result is correct; that, together with the original equation, is equivalent to y/(2x). (This is important: Your expression can’t be simplified by itself to theirs; they are only the same for (x, y) on the given curve.)
Sometimes it is possible to use the given equation to rewrite our “bad” answer and get a nicer form (that might even match the book). I didn’t try this at the time, but I see some interesting features of our original solution that make it worth doing.
We have the equation \(x^2+y^4=5xy^2\) and the derivative \(\frac{5y^2-2x}{2y(2y^2-5x)}\). Both the numerator and the denominator contain terms that look close to \(5xy^2\); what if we multiply the numerator by \(x\) and the denominator by \(y^2\), and compensate by multiplying the whole by\(\frac{y^2}{x}\)?
$$y’=\frac{\left(5y^2-2x\right)x}{2y\left(2y^2-5x\right)y^2}\cdot\frac{y^2}{x}\\=\frac{5xy^2-2x^2}{2y\left(2y^4-5xy^2\right)}\cdot\frac{y^2}{x}$$
Now we can replace \(5xy^2\) with \(x^2+y^4\), since these are the same for any point on the curve, and see what we get:
$$y’=\frac{5xy^2-2x^2}{2y\left(2y^4-5xy^2\right)}\cdot\frac{y^2}{x}\\=\frac{\left(x^2+y^4\right)-2x^2}{2y\left(2y^4-\left(x^2+y^4\right)\right)}\cdot\frac{y^2}{x}\\=\frac{y^4-x^2}{2y\left(y^4-x^2\right)}\cdot\frac{y^2}{x}\\=\frac{1}{2y}\cdot\frac{y^2}{x}=\frac{y}{2x}$$
We did it! we’ve shown that at any point on the curve, the two answers are equivalent.
3: Try to prove that our answer agrees with the book’s
But we can’t always expect to see such a path to a desired answer; we were very lucky. In the absence of that discovery, I suggested a more generally useful approach when your answer doesn’t match the book:
Now, how can you show that? You want to find a way to use the original equation to obtain theirs from yours, which is typically difficult. What you can do instead is to set your derivative equal to theirs, and “solve”. You’ll find at some point that you will have an equation related to (perhaps equivalent to) the given equation. And if you wanted to, you could reverse this work in order to obtain their answer from yours, or vice versa. (I’m not sure whether this always works, but it does in my experience, when I’ve tried. I successfully did it here.)
This idea is similar to proving an identity in trigonometry.
So here’s the work:
We want to show that $$\frac{5y^2-2x}{2y(2y^2-5x)}=\frac{y}{2x}$$
We can clear fractions (or, equivalently, cross-multiply), assuming both denominators are non-zero, and then “solve”:
$$\frac{5y^2-2x}{2y(2y^2-5x)}=\frac{y}{2x}\\2x\left(5y^2-2x\right)=y\cdot2y\left(2y^2-5x\right)\\10xy^2-4x^2=4y^4-10xy^2\\20xy^2=4x^2+4y^4\\5xy^2=x^2+y^4$$
But we already know the last line is equivalent to the given equation; so when the equation is true, the two claimed derivatives are equal. And if you read upward from the last line, you actually derive the equivalence of the derivatives from the equation.
4: Differentiate explicitly
In principle, we might also find the derivative explicitly, though this only works when you can solve for one variable:
Alternatively, the given equation can be solved for y (up to a point), and you could probably show that both answers are equivalent to the explicit derivative. (I haven’t even tried this, which would be hard, and is not usually an option.)
I said “up to a point” because we actually get multiple values for y; this isn’t a function. But it turns out that this still works.
Here’s how:
We want to solve \(x^2+y^4=5xy^2\) for y, which we can do with a little thought:
$$y^4-5xy^2-x^2=0\\y^2=\frac{5x\pm\sqrt{\left(-5x\right)^2+4x^2}}{2}=\frac{5x\pm\sqrt{29x^2}}{2}=\frac{5\pm\sqrt{29}}{2}x$$
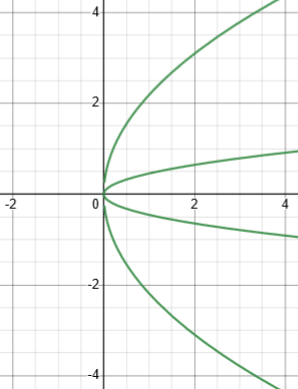
Hmmm … that’s a parabola! No, two parabolas, with different parameters. (I’ll graph them in a moment.) Do you recall what I said at the start, that an implicit equation “defines a function (or several functions)”? This is what I was talking about. Even if we solved for x as a function of y, we’d have two of them.
Furthermore, we can guess that if we change the 5 to another number, we’d just get another parabola of the form \(y^2=Ax\), or, if you prefer, \(x=\frac{1}{A}y^2\). And what is the derivative of such a parabola? $$\frac{d}{dx}\sqrt{Ax}=\frac{d}{dx}\left(Ax\right)^{1/2}=\frac{1}{2}\left(Ax\right)^{-1/2}\cdot A=\frac{A}{2\sqrt{Ax}}=\frac{\sqrt{Ax}}{2x}.$$
And this is \(\frac{y}{2x}\)! So, yes, we get the same result – and not just on our curve, but on any of this family of curves with different values of A.
5: Check the graph
In preparing for publication (and before solving as I just did above), I tried graphing the equation on Desmos, to see if that would give any insight. (This is something you can do even if you can’t solve explicitly for y – software can do amazing things!) I was surprised to see the two parabolas:
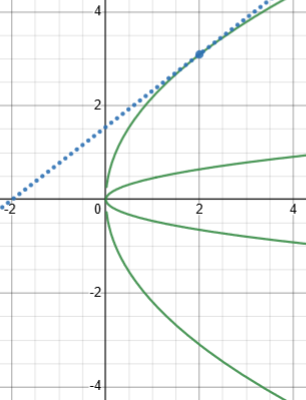
What we have determined so far is that at every point on this curve, \(y’=\frac{y}{2x}\); we could check this at a few points if we doubted our answer. For example, it approximately passes through \((2,3.1)\); there \(\frac{y}{2x}=\frac{3.1}{4}=0.775\), which looks about right. Here is that line, which appears to be tangent:
A family of curves
But what about other points not on the curve? They will lie on other members of the family of curves given by $$\frac{x}{y^2}+\frac{y^2}{x}=k,$$ where we allow the constant on the right-hand side to vary. Here is part of that family:
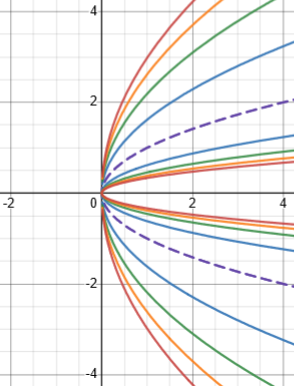
The purple broken curve represents \(k=2\); the other curves are for \(k={\color{Blue}3},{\color{Green}5},{\color{DarkOrange}7},{\color{Red}9}\). (You can imagine what might happen for larger or negative values of k. It does.) At any point on one of these lines, the derivative of that curve is given by \(y’=\frac{y}{2x}\).
Our original form for the derivative works only on our original curve, because the 5 is part of it. Note: In clearing fractions, the constant that in the straightforward approach differentiates to zero (and so disappears), gets baked into the formula, making the formula work only on that particular member of the family.
For example, at the point \((4,3.25)\), it gives \(\frac{5y^2-2x}{2y(2y^2-5x)}=\frac{5(3.25)^2-2(4)}{2(3.25)(2(3.25)^2-5(4))}=\frac{44.8125}{7.3125}\approx6.128\), which is clearly wrong:
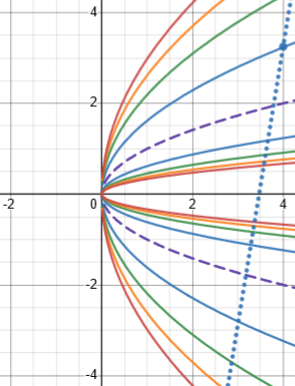
But the other formula gives \(\frac{y}{2x}=\frac{3.25}{2\cdot4}=0.40625\), which looks about right:
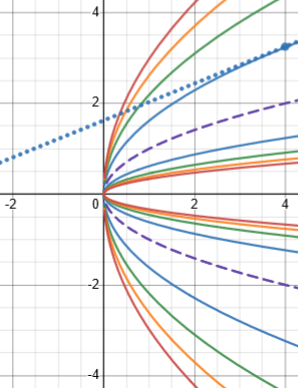
So was our original derivative wrong, in the sense that it doesn’t work for the whole family? No, it just represents a different family. Here are members of the family \(x^2+y^4=5xy^2+k\), for \(k=-100\) to \(100\). We see that the line we got for \((4,3.25)\) looks right this time:
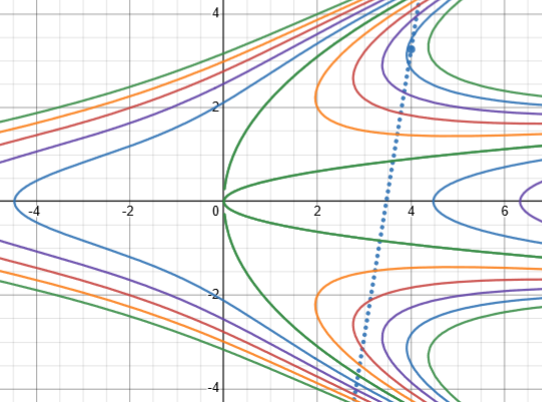
(Our point fits \(k\approx-84\), and the blue curve near it is for \(k=-80\).)
My answer seems too simple!
Looking for other questions about implicit differentiation, I found this from Lance in early 2021:
Hi,
I am given a formula 0 = 2x^2 + xy – y^2 – 6x + 3y
I have to
a) use implicit differentiation to find the derivative
b) evaluate dy/dx at the point (2,4)
c) determine the equation of the tangent to the curve at the point (2,4) expressing my answer in the form y=mx + b
When I got to (c) my answer was y=2x which looked a little straightforward.
I have attached my workings below. I just wanted to check what I have done is correct and that I did not miss anything.
Is his equation for the tangent line, \(y=2x\), too simple to be correct? No. We’ll see that it’s exactly as simple as it should be.
Here is his work for part (i):
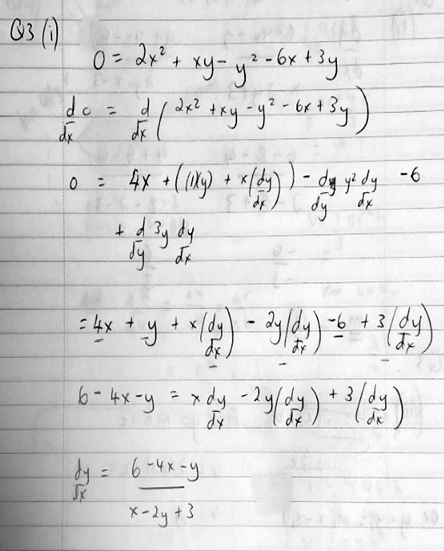
He used the chain rule and the product rule to differentiate:
$$2x^2+xy-y^2-6x+3y=0$$
$$\left(2x^2\right)’+\left(xy\right)’-\left(y^2\right)’-\left(6x\right)’+\left(3y\right)’=(0)’\\\left(4x\right)+\left(x’y+xy’\right)-\left(2yy’\right)-\left(6\right)+\left(3y’\right)=0\\4x+y+xy’-2yy’-6+3y’=0\\4x+y-6+\left(x-2y+3\right)y’=0\\y’=-\frac{4x+y-6}{x-2y+3}$$
Looks good. There was no reason to modify the equation before differentiation, so we don’t have that issue here.
Here is the rest of the work:
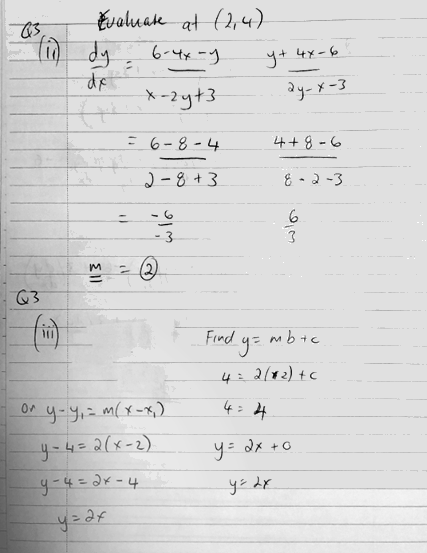
He calculated \(y’\) at \((2,4)\) twice to double-check it, and found (using my form) that $$y’=-\frac{4x+y-6}{x-2y+3}=-\frac{4(2)+(4)-6}{(2)-2(4)+3}=-\frac{6}{-3}=2$$
So for the tangent, we want the equation for a line through \((2,4)\) with slope \(m=2\). He did this, too, two ways. On the left, he uses the point-slope form \(y-y_1=m\left(x-x_1\right)\) for a line with slope m through point \((x_1,y_1)\): $$y-y_1=m\left(x-x_1\right)\\y-4=2\left(x-2\right)=2x-4\\y=2x$$
On the right, he uses slope-intercept form, which I know by the American form, \(y=mx+b\); he substitutes the coordinates for the known point, and solves for the unknown y-intercept. In my terms, this is $$y=mx+b\\4=2(2)+b\\4=4+b\\b=0$$ so the equation is, again, \(y=2x\).
Everything is correct, and doubly so. All that’s needed is some encouragement, it seems.
Look at the graph
I answered, not needing to say much, but choosing to make a graph (as above) as a quick check:
Hi, Lance.
Yes, the work is all good.
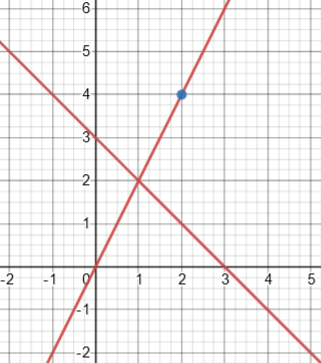
Now, I put the equation into Desmos thinking to show you that your tangent line is correct, and got a little surprise. Here is the graph:
Now that’s interesting! The tangent line is actually part of the “curve” itself.
The equation had the form of a general conic section, but the graph is a special case.
We saw a similar surprise in the last section of Implicit Differentiation: Explanation, Examples, and a Surprise, which also involved two lines.
It turns out that the graph of the equation is not an ellipse or hyperbola as I expected at first glance, but a degenerate conic section consisting of two lines, so your tangent at (2, 4) is actually part of the graph itself! But it is clearly the right “tangent”.
We discussed degenerate conic sections in Degenerate Conics I: Mystery of the Missing Case; this is the case of a pair of intersecting lines. Since the graph consists of two lines, each of those lines is itself a tangent.
So it turns out that the equation can be factored as (2x – y)(x + y – 3) = 0.
This factored form is not immediately obvious from the general form \(2x^2+xy-y^2-6x+3y=0\); I probably just read it off from the graph, writing each lines equation in standard form \(ax+by+c=0\), multiplying the left-hand sides, and checking that the product was correct. There are other tricks I could have used, one being to rotate the graph to eliminate the xy term, and then complete the squares.
So the two lines are \(2x-y=0\) and \(x+y-3=0\), which become $$y=2x\\x+y=3$$ The first of these is our tangent line.
And your derivative y’ = (6 – 4x – y)/(3 + x – 2y) agrees: When y = 2x, it simplifies to 2 (except when x = 1, when it is 0/0), and when y = 3 – x, it simplifies to -1 (except when x = 1).
So it’s a more interesting problem than either of us realized!
Here I used the equations for the separate lines to show that his formula for the derivative simplifies to the known slope of each line, on that line. When we replace y with \(2x\), we get $$y’=-\frac{4x+y-6}{x-2y+3}=-\frac{4x+2x-6}{x-2(2x)+3}\\=-\frac{6x-6}{-3x+3}=-\frac{6(x-1)}{-3(x-1)}=2$$ and when we replace y with \(3-x\), we get $$y’=-\frac{4x+y-6}{x-2y+3}=-\frac{4x+(3-x)-6}{x-2(3-x)+3}\\=-\frac{3x-3}{3x-3}=-1$$
In both cases, we canceled \((x-1)\), which is why the derivative is undefined (or, rather, indeterminate, at \(x=1\)): It actually has both slopes at that point, where the lines intersect.
Look at the whole family of curves
As before, the equation can be modified, by changing right-hand side to any constant (which doesn’t affect the derivative), making the equation $$2x^2+xy-y^2-6x+3y=k$$ Here is the graph of members of this family for \(k={\color{Red}{-4}},{\color{DarkOrange}{-2}},{\color{DarkGreen}0},{\color{Blue}2},{\color{Purple}4}\):
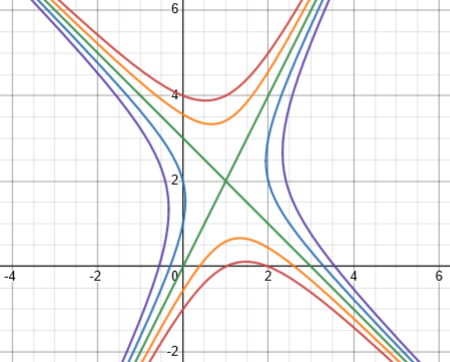
This is a family of hyperbolas (rotated from the usual orientation).
And again, our derivative formula applies to any point in the plane, giving the slope of the curve through that point. For example, at \((2,2)\), the slope is $$-\frac{4x+y-6}{x-2y+3}=-\frac{4(2)+(2)-6}{(2)-2(2)+3}=-\frac{4}{1}=-4$$ which looks about right:
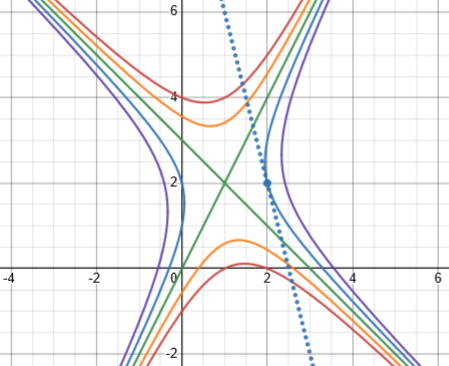
Is there any way to change this formula into something simpler? I don’t know.
Look deeper: 3D
If we graph the equation as $$z=2x^2+xy-y^2-6x+3y$$ in three dimensions (using Geogebra), we get a hyperbolic paraboloid, horizontal slices of which are the curves in this family. Here are three of the curves shown above (\({\color{DarkOrange}{z=-2}},{\color{Green}{z=0}},{\color{Blue}{z=2}}\)):
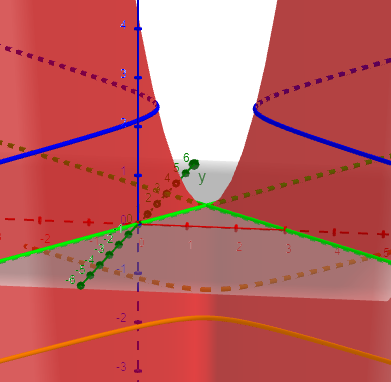
Our original equation gives the pair of lines in green, which pass through the “saddle point” of the surface.
Our implicit derivative equation gives tangents to these cross-sectional curves, which are the intersections of tangent planes to the surface with the cutting planes. There’s a lot more we could say, but I’ll stop there!
However, if you’re interested in the graph of the first problem, here it is, with cross sections at \({\color{Blue}{z=3}},{\color{Green}{z=5}}\):
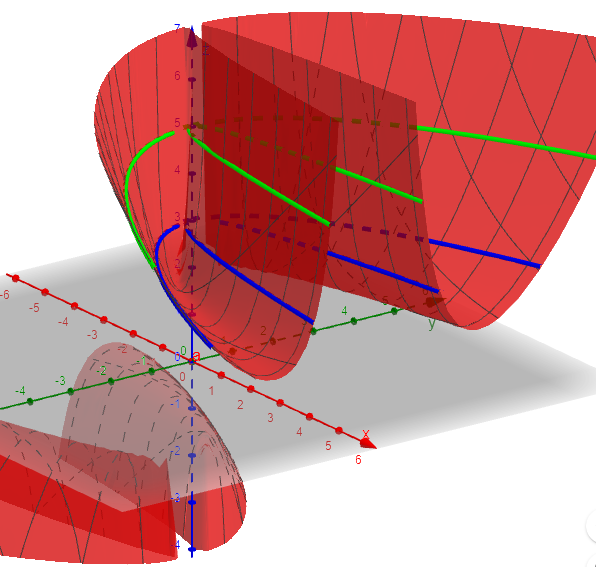
The graph is inaccurate near the z-axis, where there is more happening than the software can handle.