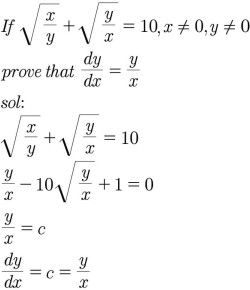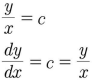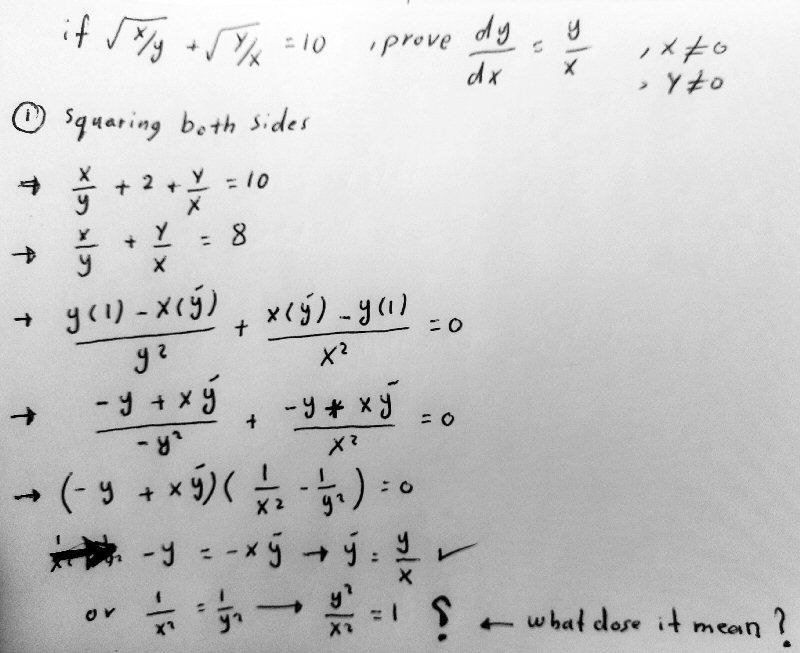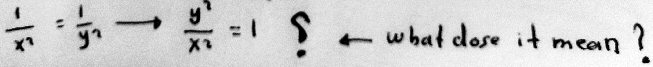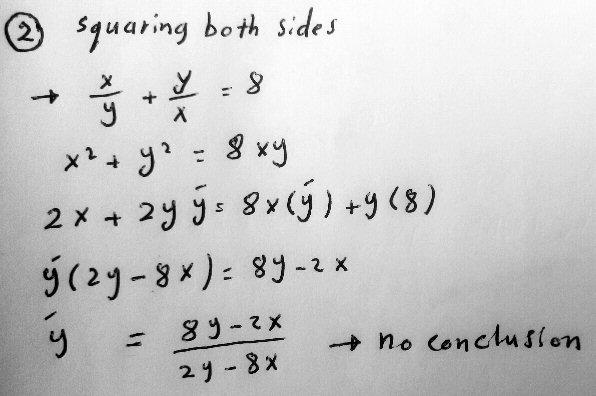(A new question of the week)
We are often asked to help a student understand a solution to a problem, obtained from a book or a website, that is not fully explained there. Here, we’ll look at a rather odd demonstration that a function satisfies a differential equation, both figuring out what the author did, and finding alternative methods that clarify what is happening.
Understanding a shortcut solution
Here is the question, from the end of August, giving a problem and solution presumably found somewhere online:
Hi Dr Math.
I want to check if the solution of the question below is acceptable? and why it assumes y/x =c?
Normally, one might just find expressions for \(\frac{dy}{dx}\) and \(\frac{y}{x}\), and show that they are equal. But this author made the work much shorter than that (though we’ll see that it could have been made even shorter!). I answered:
Hi, Amia.
That’s a very interesting problem. You are right to be suspicious, because the step you ask about is a little odd; and I hope the author wants you to think further. I don’t think the point is to teach you a method you can use for other problems; it’s very, very specific to this one.
Let’s look at it piece by piece.
First, the problem:
They are giving you an equation that implicitly defines y as a function (or functions) of x. One would normally find the derivative implicitly, which I’ll try doing at the end. But they instead take what would commonly be the long way, starting to solve the equation:
What they’ve done here is to multiply both sides by √(y/x), and collect terms on one side.
Some equations of this sort can’t be explicitly solved for y, or it can be very hard to do so, so that implicit differentiation saves work. In this case, it can be solved, as we’ll be doing later; but the author only started that process before making a surprising leap.
Filling in the gap, $$\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{x}}=10\\\sqrt{\frac{x}{y}}\sqrt{\frac{y}{x}}+\sqrt{\frac{y}{x}}\sqrt{\frac{y}{x}}=10\sqrt{\frac{y}{x}}\\1+\frac{y}{x}=10\sqrt{\frac{y}{x}}\\\frac{y}{x}-10\sqrt{\frac{y}{x}}+1=0$$
Another approach to the same thing would have been to substitute a variable u = √(y/x), changing the equation to
1/u + u = 10
which we can solve by multiplying everything by u:
1 + u2 = 10u
u2 – 10u + 1 = 0
That’s really the same result.
Such an equation is sometimes called “quadratic in form”, and can be solved with or without the substitution. Either way, the next step would be to either factor (if possible), or use the quadratic formula. But …
Now, rather than actually finish solving, they make a leap: We can solve this equation for y/x, or my equation for u, and we will end up with y/x equaling some number (actually, one of two numbers, since it’s a quadratic equation – that’s an error, but not a big one).
This same conclusion could have been reached without doing any algebra: Since the given equation can be put in the form \(f\left(\frac{y}{x}\right)=0\), any solution will have the form \(\frac{y}{x}=constant\), regardless of the type of equation! The only problem would be if the equation had no (real) solution.
And if y/x is some constant (who cares what its value is, they say; let’s just call it c), then we have a linear function, and we know what the derivative will be:
Here’s what that means, filling in the gaps: Since y = cx, dy/dx = c; but that’s just what y/x is equal to: so dy/dx = y/x, for all x and y that satisfy the equation. QED.
It feels like racing down the road, making a sudden stop, and saying, “We’re here!”
Alternative 1: Finish solving
If we skip the shortcut at the end, maybe we’ll gain a little more insight:
But what happens if we finish solving, despite the work that will entail? I’ll do it in my version:
u2 – 10u + 1 = 0
u = (10 ± √((-10)2 – 4(1)(1)))/2 = (10 ± √(96))/2 = 5 ± √24
So
√(y/x) = 5 ± √24
y/x = (5 ± √24)2 = 49 ± 20√6
y = (49 ± 20√6)x
This, surprisingly, is equivalent to the given equation!
That is, our impressive equation \(\sqrt\frac{x}{y}+\sqrt\frac{y}{x}=10\) is really just a linear equation (in fact, a proportion) in disguise. Well, two of them.
So our equation is equivalent to two functions, approximately
y = 97.9898x
y = 0.0102x
So those are the actual values of c. And the derivative is, in fact, 97.99 or 0.0102, which is equal to y/x in each case.
So yes, their work is valid; but it could have used a fuller explanation.
The differential equation that was our goal is in fact satisfied by any straight line passing through zero, since if \(y=cx\), then \(\frac{dy}{dx}=c\), and \(\frac{y}{x}=c\) also. That is, the instantaneous rate of change at \((x,y)\) is the same as the average rate of change from \((0,0)\) to \((x,y)\).
Graphing the equation to make it visible
I tried putting the original equation into GeoGebra and it showed almost nothing; only when I stretched the axes greatly could I see the graph, probably due to some sort of rounding error or overflow in the calculation. It does work on Desmos, except near the origin:
So it is a valid implicit function, and the derivative at any point is a constant (one of two), and the derivative at any point on the graph is equal to y/x.
We can see why the method we are examining is very specific to this particular (type of) equation. How about other ways?
Alternative 2: Implicit differentiation
Now I did what I had suggested felt normal:
Let’s try using implicit differentiation and see if we can do the same thing. The equation can be written as
x1/2y-1/2 + x-1/2y1/2 = 10
Differentiating, we get
(1/2)x-1/2y-1/2 + x1/2(-1/2)y-3/2y’ + (-1/2)x-3/2y1/2 + x-1/2(1/2)y-1/2y’ = 0
Solving for y’,
(1/2)x-1/2y-1/2 – (1/2)x1/2y-3/2y’ – (1/2)x-3/2y1/2 + (1/2)x-1/2y-1/2y’ = 0
x-1/2y-1/2 – x-3/2y1/2 = x1/2y-3/2y’ – x-1/2y-1/2y’
x-1/2y-1/2 – x-3/2y1/2 = [x1/2y-3/2 – x-1/2y-1/2]y’
y’ = [x-1/2y-1/2 – x-3/2y1/2] / [x1/2y-3/2 – x-1/2y-1/2]
Multiplying numerator and denominator by x3/2y3/2, we get
= [xy – y2] / [x2 – xy]
= [y(x – y)] / [x(x – y)]
= y/x [as long as y ≠ x]
Same answer, more work.
(The restriction that \(y\ne x\), in order to cancel, is no problem, because if \(y=x\), then the original equation would be \(1+1=10\), so the point clearly would not satisfy the equation.)
I was actually a little surprised that we ended up with the desired form so easily, because implicit differentiation can yield very different-looking answers because of the dependence on both x and y. We’ll see that later.
But implicit differentiation tends to miss details – such as the fact that y/x only has one of two values anywhere.
If you know anything about differential equations, however, you can solve dy/dx = y/x and you’ll find that all solutions have the form y = cx, for some value of c.
Let’s do that: $$\frac{dy}{dx}=\frac{y}{x}\\\frac{dy}{y}=\frac{dx}{x}\\\int\frac{dy}{y}=\int\frac{dx}{x}\\\ln(y)=\ln(x)+C\\y=e^{\ln(x)+C}=e^{\ln(x)}e^{C}=cx$$
Alternative 3: Square before differentiating
Two days later, Amia wrote again about the same problem, this time presenting his own attempts (which I will show one at a time):
Hi Dr Math,
I asked this question before, but every time I try to solve it, I found strange things. Can you check with me some of my solutions?
In case you have trouble following some details, I’ll fill in a couple gaps. Here is what happens when we square the equation: $$\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{x}}=10\\\left(\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{x}}\right)^2=10^2\\\left(\sqrt{\frac{x}{y}}\right)^2+2\left(\sqrt{\frac{x}{y}}\sqrt{\frac{y}{x}}\right)+\left(\sqrt{\frac{y}{x}}\right)^2=100\\\frac{x}{y}+2+\frac{y}{x}=100\\\frac{x}{y}+\frac{y}{x}=98$$
We’ve discovered a small error in the work (forgetting to square the right-hand side), which won’t have a major effect (yet), because the constant will disappear when we differentiate. The differentiation is straightforward, using the quotient rule and then factoring out the shared numerator. The first factor yields the desired result; he asks about the significance of the other?
He included a second solution, which I’ll show after discussing this one.
I replied:
Hi, again, Amia. I’m glad you have the curiosity to continue investigating this very interesting problem!
First, you did well when you squared the equation (nice idea!). The only missing piece is your question at the end,
What it means is that the conclusion that y’ = y/x need not be true if x2 = y2. But we’ve already seen that the given equation represents a pair of lines that intersect at the origin, so the only case where this will be true is when x = y = 0. But that is excluded in the problem.
The factored result showed that either \(y’=\frac{y}{x}\) or \(x^2=y^2\), so if the latter is true, the former need not; but the latter is a pair of lines \(y=\pm x\) that intersect the graph of the given equation only at the origin.
If we didn’t know the graph, we could simply replace y with x or -x and see that the original equation couldn’t be true. The LHS would be either 2 or 2i, which are not equal to 10.
Replacing \(y\) with \(x\), the equation becomes $$\sqrt{\frac{x}{x}}+\sqrt{\frac{x}{x}}=10\\1+1=10$$ so such a point can’t satisfy the equation; and replacing \(y\) with \(-x\), the equation becomes $$\sqrt{\frac{x}{-x}}+\sqrt{\frac{-x}{x}}=10\\i+i=10$$ with the same conclusion. The claim about the derivative applies only to points that satisfy the equation; and no such point makes our second factor zero, so it must do so for the second factor.
So this method was entirely successful.
Alternative 4: Clear fractions after squaring
Here is the second attempt:
This time, after the squaring (which should yield 98 rather than 8, as we saw above), we’ve multiplied by \(xy\) to clear fractions before differentiating. Here is the corrected work:
$$\frac{x}{y}+\frac{y}{x}=98\\\frac{x}{y}\cdot xy+\frac{y}{x}\cdot xy=98\cdot xy\\x^2+y^2=98xy.$$ Differentiating, $$2x+2yy’=98xy’+98y\\y'(2y-98x)=98y-2x\\y’=\frac{98y-2x}{2y-98x}=\frac{49y-x}{y-49x}.$$ This hasn’t resulted in the desired form.
As for the second attempt, I can first point out that the equation x2 – 8xy + y2 = 0 can be factored (using the quadratic formula) as
(x – (4+sqrt(15))y)(x – (4-sqrt(15))y) = 0
which is, again, the equation of two straight lines. And for each line, just as we saw last time, y’ = y/x.
That, of course, doesn’t answer your question, which is whether there is anything you can do next after finding that
y’ = (8y-2x)/(2y-8x) [ = (4y-x)/(y-4x) ]
Since I hadn’t yet noticed that the 8 is wrong, we need to correct that factorization:
$$x^2-98xy+y^2=0\\(x-(49+20\sqrt{6})y)(x-(49-20\sqrt{6})y)=0,$$ which you can check by multiplying.
So the graph consists of the two lines $$x=(49+20\sqrt{6})y\\x=(49-20\sqrt{6})y,$$ which are equivalent to the lines we saw before.
My first answer is that this doesn’t surprise me. Implicit differentiation can result in very different looking formulas when you process the problem differently before differentiating. This is because the implicit derivative by nature doesn’t explicitly take into account the fact that x and y are related; if we were to solve for y and plug that into the different expressions we get for the derivative, to get a formula in terms of x (rather than both x and y), we would find that they agree. [This is a danger in assigning implicit differentiation problems, because anything special that you do before differentiating, no matter how wise, may result in your answer being different from what the teacher expects!]
I advise students not to make such a manipulation, even though it might be a wise thing to do, simplifying the work. Here, the equivalent problem is that we get a different form than we wanted.
For more on implicit differentiation, ending with an example reminiscent of ours, see
Implicit Differentiation: Explanation, Examples, and a Surprise
In this case, taking the correct result of the work, $$y’=\frac{49y-x}{y-49x},$$ if we substitute a solution for \(y\) such as \(y=(49+20\sqrt{6})x\), we get $$y’=\frac{49(49+20\sqrt{6})x-x}{(49+20\sqrt{6})x-49x}=\frac{49(49+20\sqrt{6})-1}{20\sqrt{6}}\\=\frac{2400+980\sqrt{6}}{20\sqrt{6}}=\frac{120+49\sqrt{6}}{\sqrt{6}}=20\sqrt{6}+49,$$ which is equal to \(\frac{y}{x}\). But we don’t really need to work with the actual numbers:
In our case, knowing from before that y = cx (and not worrying about its value for the moment, just as before), your result becomes
y’ = (8cx-2x)/(2cx-8x) = (4c-1)/(c-4)
If you take the value(s) of c we found before, I think you’ll find that this is equal to c, which is equal to y/x. I’ll leave that for you to try.
I hadn’t noticed that the value 8 was wrong, but we’ve seen above that it does work with the right numbers.
Can we obtain the desired result without solving?
But we generally do implicit differentiation because we can’t solve for y, or at least (as in this problem) we chose not to do that work. Is there anything we could do without solving, to turn your result into y/x?
I am going to leave this as a challenge for you (frankly, because I don’t quite see it yet, and have already spent more time having fun with this than I intended …). The basic idea will be to try somehow combining the expression for y’ with the original equation (in one form or another, likely your squared form) to turn it into y/x.
It turns out not to be hard:
The given equation, after squaring, was $$x^2+y^2=98xy.$$ Our derivative is $$y’=\frac{49y-x}{y-49x}.$$ Manipulating the equation to obtain the numerator and denominator, we find that $$49y-x=\frac{98xy-2x^2}{2x}=\frac{y^2-x^2}{2x}\\y-49x=\frac{2y^2-98xy}{2y}=\frac{y^2-x^2}{2y}.$$ Therefore, $$y’=\frac{49y-x}{y-49x}=\frac{\frac{y^2-x^2}{2x}}{\frac{y^2-x^2}{2y}}=\frac{y}{x}.$$
Can we prove the desired result without solving?
But we are given the result we want, so we don’t have to derive it as if we didn’t know what to expect!
Or, since the original problem was to show that y’ = y/x (that is, you were given a result and told to prove it), you can take the equation
(8y-2x)/(2y-8x) = y/x
and show that it is true given the given equation. There may be several ways to do this; or it may still be difficult. The main thing to know is that this sort of thing is normal with implicit differentiation; the fact that you didn’t get the result they asked for is not surprising, and doesn’t mean you’ve done anything wrong. In fact, this is a thought I had when I first saw the problem: To expect you to find a particular form for the derivative without knowing their trick would be unfair. That’s part of the reason I was so pleased with what I was able to do with it!
Let’s try this, too. Given the (corrected) equation $$\frac{49y-x}{y-49x}=\frac{y}{x},$$ we can cross-multiply to get $$49xy-x^2=y^2-49xy\\98xy=x^2+y^2,$$ which is in fact equivalent to our equation, and therefore true for all such points!
Yet another solution: total differential
Amia then found another solution online:
I have this solution, can you help me to understand.
He found this on Quora; a little questioning revealed that Amia has not learned about the total differential, and there is no further context to the question or answer.
I answered, trying to give a quick explanation of the concept:
The total differential can be described in various ways, some far more convoluted than others; and I’m not quite sure of this author’s reason for using it.
So, what is it? Here’s one textbook introduction to the idea (just read the beginning). It provides a way to approximate values of a function of two (or more) variables, in effect by giving an equation of the tangent plane. Think of dx and dy as (small) coordinates representing offsets from (x,y).
If we follow a level curve of the surface z = F(x,y) (along which z is constant), we will be moving along the surface at a constant height, always moving horizontally; so dF will be 0. So, the tangent line to the curve will go in a direction, given by a vector <dx,dy>, in which z remains constant. And the ratio dy/dx will be the slope of this curve in the xy-plane.
What they are doing is writing the given equation as F(x,y) = 10, and finding the total differential of the LHS, which, as they say, will be zero for our curve.
(I’ve corrected here a major error in my explanation – sorry, Amia!)
In general, the graph of \(z=F(x,y)\) is a surface, and \(F(x,y)=c\) is a level curve of that surface, which in our case is always a pair of lines. Here is what this looks like for \(c=4\):
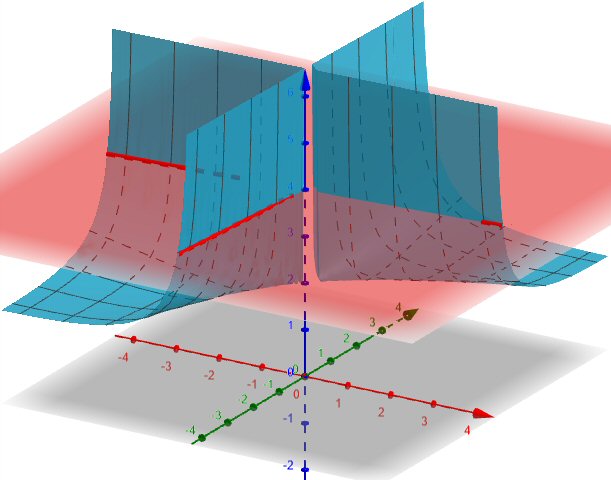
I chose not to show \(F(x,y)=10\), representing our problem, because GeoGebra, as I mentioned for the 2D case, has trouble showing that intersection, and this one looks better than others. Even here, you shouldn’t be able to see pink through the middle of the surface, and the red lines should extend to the axis! But this gives some sense of how our curve relates to the surface.
So the total differential, which describes the tangent plane, intersects the horizontal plane along a line that is tangent to the level curve. (In our case, it is identical to the level curve!) Its slope, \(\frac{dy}{dx}\), is the derivative of the level curve. That’s what Francesco was doing.
Amia replied:
Thank you Dr Peterson,
I have a question why we write F(x,y) = 10? Not zero ?
Why we don’t write the equation in form F(x,y) = 0?
Why we don’t write it F(x,y) = sqrt(x/y) + sqrt(y/x) – 10?
I responded,
Those could be good questions to ask Francesco!
But rather than ask “why [must] we write …”, the question to ask is “why did you write …”. I say that because what he chose to do is not the only way he could have done this; it is just one way. Your alternative is probably just as good.
The one advantage I see in his choice is that he only needs F(x,y) to be some constant, and putting the 10 on the RHS saves a little writing.
But as I have often said, when you wonder why something is or was done, and not something else, the best thing to do is to try the alternative yourself and see what happens. Typically you will either find out why (and gain understanding), or find out that it doesn’t matter (and discover a freedom you didn’t know you had).
There was no further reply, so I didn’t get to discuss more about this.