We’ve been looking at the commutative, associative, and distributive properties of operations, starting at an introductory level. But why are these properties important? Why do they have names in the first place? And what other operations have them?
Who invented these properties?
Here is a question from 2001:
History of Properties I really wonder who invented the properties. For example the distributive property and associative property.
I answered:
Hi, Noah. These properties have always been there, and have probably been used since ancient times; for example, any method of multiplying digit by digit uses the distributive property. But it makes sense to ask who first recognized these properties as something worth talking about.
Who named them?
One question to ask, then, is who came up with those names for the properties. You can find such questions answered at Jeff Miller's site, which is listed in our FAQ under Math History:
Earliest Uses of Some Words of Mathematics
http://jeff560.tripod.com/mathword.html
This site has moved, so I updated the link.
Looking up "distributive" and "associative," I find this: ASSOCIATIVE "seems to be due to W. R. Hamilton" (Cajori 1919, page 273). Hamilton used the term as follows: However, in virtue of the same definitions, it will be found that another important property of the old multiplication is preserved, or extended to the new, namely, that which may be called the associative character of the operation.... The citation above is from "On a New Species of Imaginary Quantities Connected with the Theory of Quaternions," Royal Irish Academy, Proceedings, Nov. 13, 1843, vol. 2, 424-434. COMMUTATIVE and DISTRIBUTIVE were used (in French) by Francois Joseph Servois (1768-1847) in a memoir published in Annales de Gergonne (volume V, no. IV, October 1, 1814). He introduced the terms as follows (pp. 98-99): [long quotation in French, not about addition or multiplication, but about "functions" or "operators" in general]
Quaternions were a new kind of “number” inspired by complex numbers.
Here is a Google translation of the quotation (with corrections where I can tell it is inadequate):
3. Let
\(f(x+y+…)=fx+fy+…\)
The functions which, like f, are such that the function of the (algebraic) sum of any number of quantities is equal to the sum of the like functions of each of these quantities, will be called distributive.
So, because
\(a(x+y+…)=ax+ay+…; E(x+y+…)=Ex+Ey+…; …\)
the factor ‘a’, the varied state E, … are distributive functions; but, as we do not have
\(\sin.(x+y+…)=\sin.x+\sin.y+…; L(x+y+…)=Lx+Ly+…; \)
… the sines, the natural logarithms, … are not distributive functions.
4. Let
\(fgz=gfz.\)
The functions which, like f and g, are such that they give identical results, whatever the order in which they are applied to the subject, will be called commutative between themselves.
Thus, because we have
\(abz=baz;aEz=Eaz;…\)
the constant factors ‘a’, ‘b’, the constant factor ‘a’ and the varied state E, are commutative functions between themselves; but since ‘a’ is always constant and ‘x’ variable, we do not have
Sin.az = a Sin.z; Exz = xEz; Dxz = xDz [D = delta]; …
it follows that the sine with the constant factor, the varied state or the difference with the variable factor, … do not belong to the class of commutative functions between them.
So these terms arose in the early 1800's, when mathematicians were starting to analyze more abstract kinds of objects than numbers (such as quaternions and functions, in these examples), and needed to talk about which of the properties of numbers also worked for these objects. I'm sure that the developers of algebra in its early form must have been aware of these properties to some extent, but they didn't speak about them in the same terms.
You don’t need a name for a fact that is well-known and universal; you do need a name for something that may or may not be true.
What was the context?
Looking for more historical details, I went to
The MacTutor History of Mathematics archive
http://www-history.mcs.st-and.ac.uk/
which is also listed in our FAQ. Searching for the word "distributive," I found this about George Boole:
In 1854 he published _An investigation into the Laws of Thought, on Which are founded the Mathematical Theories of Logic and Probabilities_. Boole approached logic in a new way reducing it to a simple algebra, incorporating logic into mathematics. He pointed out the analogy between algebraic symbols and those that represent logical forms. It began the algebra of logic called Boolean algebra which now finds application in computer construction, switching circuits etc.
Boole also worked on differential equations, the influential _Treatise on Differential Equations_ appeared in 1859, the calculus of finite differences, _Treatise on the Calculus of Finite Differences_ (1860), and general methods in probability. He published around 50 papers and was one of the first to investigate the basic properties of numbers, such as the distributive property, that underlie the subject of algebra.
A more recent article on the same site shows his laws explicitly:
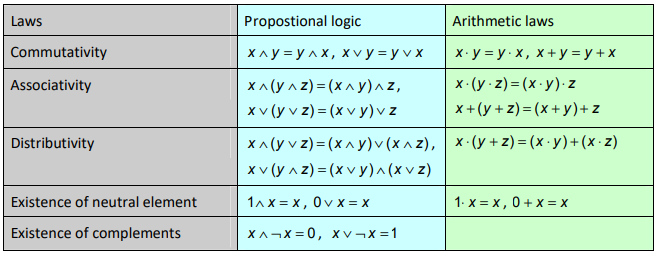
Here \(\wedge\) means “and”, and \(\vee\) means “or”.
He, too, was studying new objects that follow rules similar to those of numbers, particularly logic (treating "true" and "false" as numbers).
Note above that, unlike addition and multiplication, “and” and “or” each distribute over the other!
A little earlier, there is George Peacock: In 1830 he published _Treatise on Algebra_ which attempted to give algebra a logical treatment comparable to Euclid's _Elements_. He has two types of algebra, arithmetical algebra and symbolic algebra. In the book he describes symbolic algebra as the science which treats the combinations of arbitrary signs and symbols by means defined through arbitrary laws. He also said We may assume any laws for the combination and incorporation of such symbols, so long as our assumptions are independent, and therefore not inconsistent with each other. Peacock extended the rules of arithmetic using what he called the principle of the permanence of equivalent forms to give his symbolic algebra, so he was not as bold in practice as the abstract ideas for symbolic algebra which he gives in theory. He investigated the basic properties of numbers, such as the distributive property, that underlie the subject of algebra.
The current version of this page adds:
This property allowed Peacock to ‘prove’ that (-1)(-1) = 1, and it would appear that his attempt is more convincing that earlier attempts, for instance by Euler. Peacock’s proof, which is in the second edition of the book, published in 1845, goes as follows:
\((a-b)(c-d)=ac+bd-ad-bc\) holds for arithmetic when \(a>b\) and \(c>d\). By the principle of permanence, this holds in symbolic algebra. Put \(a=0,c=0,b=1\), and \(d=1\) to get \((-1)(-1)=1\).
(Note that he is extending rules for positive numbers to apply to negatives, as we did here.)
So, again, these properties were not carefully investigated until mathematics had reached this point in its development, where properties that had previously been assumed needed to be talked about clearly in order to make algebra rigorous and allow for study of alternative kinds of "algebra." I think this gives a pretty good answer to your question: the properties we teach were first examined closely between 1810 and 1860 by a number of mathematicians who were investigating the logical basis of algebra and working on ways to extend it. Before then, they were used, but perhaps not discussed much.
For more on these ideas, see Properties as Axioms or Theorems.
Like inventing gravity
In 2002, another student asked a similar question:
I need to know the inventors of the commutative property and how they came to use it.
I replied again, giving a link to the previous answer (into which this was edited) and commenting further:
Hi, Mollie. As you'll see from [the above], it's tricky to define what you mean by "inventing" such a property. It might be compared to "inventing" the law of gravity: it's always been there, and has even always been used, yet it was not recognized as a rule worth thinking about (and as something that moves not only rocks but the whole universe) until the right person came along. The same is true here: people knew that 2+3 = 3+2 since ancient times, but eventually people realized that this was a general property that could be ascribed to operations other than addition and multiplication, and then it became something worth naming. But it was not a single person who made this discovery. If you have any further questions, feel free to write back.
Aren’t subtraction and division commutative and associative?
Here is a question from 2008, applying commutativity and associativity to subtraction and division, and clarifying their meaning:
Are Subtraction and Division Commutative and Associative Operations? Math sources (textbooks, teachers, even this website) always say subtraction and division are neither associative nor commutative. But defined properly, they plainly are both associative and commutative. So why does everyone say they're not? I'll use the commutativeness of subtraction as an example; the other situations are analogous. The expression "a - b" is defined as "a + (-b)" for any real number. see, e.g., Keedy/Bittinger/Beecher, "Algebra and Geometry," Sixth Ed'n, at p. 8, Theorem 2. That expression commutates beautifully: a + (-b) = (-b) + a 2 + (-3) = (-3) + 2 Thus, given the definition of subtraction, the statement that subtraction is not commutative is false. The statement appears to result solely from the obvious fact that the statements "a + (-b)" and "b + (-a)" are different. But isn't that just being willfully sloppy about the meaning of the "-" sign? In other words, even with a minimum of care about what the signs mean, the alleged non-associativeness and non-commutativeness of subtraction and division (with "a divided by b" defined as "a x 1/b", (see Keedy/Bittinger/Beecher at p. 9, Theorem 4) vanishes. So why does everyone insist that these operations are in fact non-commutative and non-associative? Incomprehensibly to me, this even includes the Keedy/Bittinger/Beecher textbook on p. 10, problems 75-78.
Are all the textbooks wrong? Or is Uli misunderstanding what the properties mean?
I answered:
Hi, Uli. You wrote: >Math sources (textbooks, teachers, even this website) always say >subtraction and division are neither associative nor commutative. But >defined properly, they plainly are both associative and commutative. >So why does everyone say they're not? Because AS A BINARY OPERATION, they are not. In order to apply these properties to them, you have to rewrite them (at least in your head) as additions and multiplications. We say that an operation "#" is commutative if for any a and b, a # b = b # a If we take # as "-", then it is NOT true that a - b = b - a and that is all we are saying when we say that it is not commutative. It does not fit the definition of commutativity, applied directly. And this definition applies to the literal symbolism of an operation, not to some alternate way of thinking of it.
This is important! His thinking about how to work with subtraction and division is correct (see here), but the property is not defined that way.
>I'll use the commutativeness of subtraction as an example; the other >situations are analogous. The expression "a - b" is defined as "a + >(-b)" for any real number...that expression commutates beautifully: > >a + (-b) = (-b) + a >2 + (-3) = (-3) + 2 What you're doing here is commuting the ADDITION, not the subtraction. That's fine; this is what anyone who is good at math does automatically. But you have to call it what it is. Commuting the subtraction would mean commuting the minuend and subtrahend (a and b), not the two addends (a and -b). The fact that subtraction and division are not associative or commutative when treated (naively, one might say) as operations in themselves (simply taking the symbols as given) is the reason we teach that subtraction should be thought of as addition of the negative, and division as multiplication by the reciprocal. That is, we DEFINE subtraction as an addition so that we can use the nice properties of the latter operation, and not have to treat subtraction in practice as an operation in itself. So there is nothing inconsistent in a text saying both things.
In other words, Uli’s thinking is an appropriate work-around for the non-commutativity and non-associativity of subtraction and division, not a valid denial of these facts.
The same things happen with the associative property, which says that $$(a\#b)\#c=a\#(b\#c).$$
If it applied to subtraction and division, these pairs would be equal:
$$(9-7)-4=2-4={\color{Red}{-2}}\text{, but }9-(7-4)=9-3={\color{Red}6}$$
$$(12\div3)\div2=4\div2={\color{Red}2}\text{, but }12\div(3\div2)=12\div\frac{3}{2}={\color{Red}8}$$
But in practice we evaluate them as addition and multiplication, which are associative:
$$(9-7)-4=(9+-7)+-4=2+-4={\color{Red}{-2}}\\\text{ and }9+(-7+-4)=9+-11={\color{Red}{-2}}$$
$$(12\div3)\div2=\left(12\times\frac{1}{3}\right)\times\frac{1}{2}=\left(4\right)\times\frac{1}{2}={\color{Red}2}\\\text{ and }12\times\left(\frac{1}{3}\times\frac{1}{2}\right)=12\times\left(\frac{1}{6}\right)={\color{Red}2}$$
Uli replied:
Thank you!!! A little background clarifies everything. You wrote, "we DEFINE subtraction as an addition so that we can use the nice properties of the latter operation, and not have to treat subtraction in practice as an operation in itself." That's refreshingly honest and accurate, and extremely helpful as I help my daughter with her beginning algebra and in the process work through a number of questions I never got answered when I was in school. I really appreciate your taking the time to answer me so thoroughly. What a wonderful institution Dr. Math is!
I responded,
Hi, Uli. Thanks! This is just what we're here for; often a perspective that is not commonly taught in schools can make a big difference, and the way we get questions outside of the classroom context makes it easier to see them in different ways. One thing I've learned from doing this over the years is that, as important as definitions are in math, they are important as a TOOL, which we design to meet a specific need, and consequently we can rework them as needed in order to "sharpen" them, rather than holding on to the first way they were defined. In this case, the idea of subtraction existed before the idea of negative numbers, but when it was rethought as the addition of the negative (opposite), it made a lot of work far easier than it had been previously.
That is, subtraction was originally defined by $$a-b=c\text{ when }a=b+c$$ without reference to negatives; but defining it as $$a-b=a+(-b)$$ made everything clearer.
How about the distributive property?
Moving on to the distributive property, consider this question from 2006:
Applying the Distributive Property to Division or Subtraction The distributive property is easily shown with multiplication and addition. Can it be used with subtraction or division? I think it works sometimes but not all the time. So, does it only apply sometimes?
I answered:
Hi, Elena. The distributive property does work for multiplication over subtraction: a(b - c) = ab - ac (a - b)c = ac - bc
For example, $$2(7-3)=2\cdot4={\color{Red}8}\text{, and }2\cdot7-2\cdot3=14-6={\color{Red}8},$$ and $$(2-7)\cdot3=-5\cdot3={\color{Red}-15}\text{, and }2\cdot3-7\cdot3=6-21={\color{Red}-15}.$$
But you can only distribute division over addition (or subtraction) in one direction: a/(b + c) = a/b + a/c is false (a + b)/c = a/c + b/c is true
For example, $$\frac{12}{2+4}=\frac{12}{6}={\color{Red}2}\text{, but }\frac{12}{2}+\frac{12}{4}=6+3={\color{Red}9},$$ so the first property fails. But for the latter, $$\frac{12+4}{2}=\frac{16}{2}={\color{Red}8}\text{, and }\frac{12}{2}+\frac{4}{2}=6+2={\color{Red}8}.$$ In fact, this is how we add fractions: $$\frac{3}{6}+\frac{2}{6}=\frac{3+2}{6}=\frac{5}{6}.$$
This is most easily understood if you do as mathematicians do, and think of subtraction as adding the opposite, and of division as multiplying by the reciprocal. Then the subtraction cases above really mean this: a(b - c) = a(b + -c) = ab + a(-c) = ab + -ac = ab - ac (a - b)c = (a + -b)c = ac + (-b)c = ac + -bc = ac - bc So we are really just distributing multiplication over addition.
So changing addition to subtraction (on the inside) doesn’t mess things up.
The second [valid] case for division works this way: (a + b)/c = (a + b) * (1/c) = a*(1/c) + b*(1/c) = a/c + b/c So there we are just distributing multiplication BY the reciprocal. But this doesn't work in the other case: a/(b + c) = a * 1/(b + c) and there is no rule to simplify the reciprocal of a sum.
One-sided distributive properties, other operations
There’s a little more that can be said about this. Here is a 2007 question:
What Does It Mean to Distribute I understand the basics of the distributive property but I don't understand all the different parts of it, like there's the distributive property of multiplication over addition and over subtraction and the distributive property of division over addition. And something with square roots distributing over multiplication and over addition. I have a worksheet and I have no idea. I just don't understand all the different parts of the property. What does something distributing over something else mean? (I.e. division distributing over addition.)
I answered:
Hi, Andrea. I wouldn't call these different "parts" of one property; they are equivalent properties of different operations. In general, we say that one operation, "@", distributes over another, "#", if a @ (b # c) = (a @ b) # (a @ c) for all a, b, c and, on the other side, (a # b) @ c = (a @ c) # (b @ c) That is, doing @ on the result of # gives the same result as doing @ first to EACH element and then combining them with #. The idea of distribution is just like "distributing" money to a group of people: we give the same amount to EACH of them.
The first case would be called left-distribution, and second right-distribution.
Now, we have to consider each pair of operations separately; some operations distribute over others, and some don't. To test it, write the statements above using the given operations, and decide whether each is always true. Among the pairs that do have this property, as you mentioned, are
multiplication over addition: a*(b + c) = a*b + a*c
(a + b)*c = a*c + b*c
multiplication over subtraction: a*(b - c) = a*b - a*c
(a - b)*c = a*c - b*c
Those are what we usually call the distributive property.
Among those that DON'T distribute (on the left) are division over addition: a/(b + c) = a/b + a/c -- no exponentiation over multiplication: a^(b * c) = a^b * a^c -- no exponentiation over division: a^(b / c) = a^b / a^c -- no But these do distribute on the right: division over addition: (a + b)/c = a/c + b/c exponentiation over multiplication: (a * b)^c = a^c * b^c exponentiation over division: (a / b)^c = a^c / b^c We don't usually bother talking about this property for operations that are not commutative, because this sort of detail is confusing.
Addition and multiplication are commutative; subtraction, division, and exponentiation are not (fully).
Since a square root is really the 1/2 power, you can talk about it distributing:
root over multiplication: (a * b)^(1/2) = a^(1/2) * b^(1/2)
sqrt(a * b) = sqrt(a) * sqrt(b)
Since the square root is a unary operation, this is a little different.
Andrea replied,
Thank you so much - you've made my day! And I totally get it now! This makes so much more sense! Thank you so so so...much!
