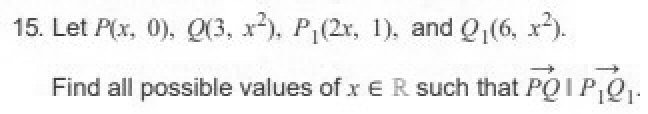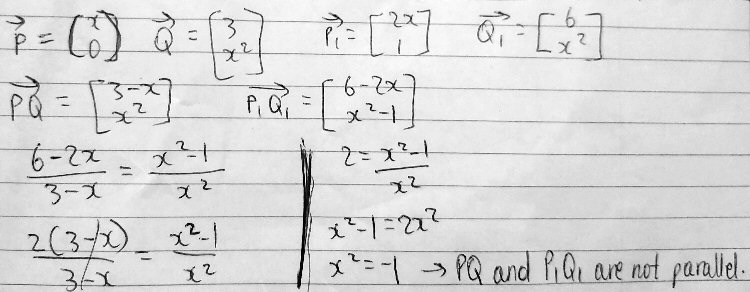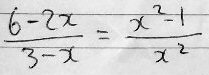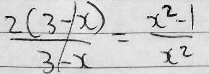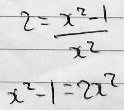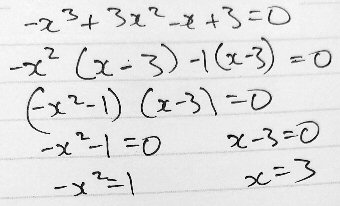(A new question of the week)
We were recently asked to check work on an interesting little question about parallel vectors, and I was almost convinced that there was no solution … until I realized there was one! How was it missed? How can we avoid doing that? That’s our goal today.
When will these vectors be parallel?
Here is the question, from Brine in mid-September:
Can you please check if my answer is correct? Thank you.
Here is my work:
Brine is using column-vector form for the vectors; I’ll be using the more compact bracket notation for convenience.
He’s found the vectors \(\overrightarrow{PQ}=\left\langle3,x^2\right\rangle-\left\langle x,0\right\rangle=\left\langle3-x,x^2\right\rangle\) and \(\overrightarrow{P_1Q_1}=\left\langle 6,x^2\right\rangle-\left\langle2x,1\right\rangle=\left\langle6-2x,x^2-1\right\rangle\), and then wrote an equation to say that the components of the two vectors are proportional: $$\frac{6-2x}{3-x}=\frac{x^2-1}{x^2}$$ Solving this yields only an imaginary solution, so it appears to be impossible for the vectors to be parallel.
I answered:
Hi, Brine.
So your answer is, that there is no such real number x?
Your work almost had me convinced, until I tried solving a different way, and saw that there is an answer.
Look carefully at your work, and think about whether there is any step in which you made an unstated assumption …
How to recognize unstated assumptions
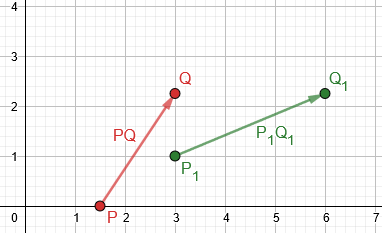
I had graphed the situation in GeoGebra, in such a way that I could vary x and observe the two vectors, to see how the problem worked, expecting perhaps to see why there would be no solution. Here is the case \(x=1.5\), for example:
But I found that I could make them parallel (as we’ll see below). That gave me reason to look more closely at the work. I’d been fooled by following along with his work rather than starting from scratch to solve the problem myself. (That’s a risk even when you check over your own work, because your mind will follow the same paths again. I should have known better, and I soon did!)
Brine replied,
I tried again but unfortunately I keep ending up that they are not parallel. Can you please give me a hint?
I answered with a more detailed hint:
As I said before, “think about whether there is any step in which you made an unstated assumption“. Here are several points in your work that you should think about:
First, you wrote this equation to say that the vectors are parallel:
When can’t you write such an equation? What fact are you using to justify the equation?
Second, here you canceled to simplify a fraction. When can’t you cancel?
Or you could think of this more generally as a rational equation. What is the domain of this equation? What does simplifying change?
Third, here you multiplied both sides of an equation. When can’t you do that?
Not all of these represent actual errors in your work; but they represent situations where you are making unstated assumptions, or ignoring special cases.
Thinking about exactly what you are doing, and what justifies each step, can be a valuable exercise when you have a wrong (extraneous or missing) solution. The answers to my questions are …
- He’s justifying the proportion because parallel vectors have proportional components … but that isn’t true when any of those components are zero.
- You can’t cancel when the factor you cancel can be zero.
- Simplifying by canceling can change the domain, introducing extraneous roots that are valid in the new equation, but are not in the domain of the original.
- You can’t multiply an equation by a factor that might be zero, because the new equation may be true when the original is not.
Which is the key issue? We’ll see.
Examples
The same sorts of problems can arise in more familiar problems, so I pointed out a couple examples:
For a similar issue, when you want to check whether two lines are parallel, you have to consider two cases: Either their slopes are equal or … what?
For another similar issue, consider how to solve an equation like x2 = 2x. It seems obvious that you can divide by x and get x=2; but that misses a solution. Why? Because you might be dividing by 0, which isn’t legal. When you divide by x, you are implicitly assuming that x≠0, which you don’t know to be true. The better way is to rearrange and factor: x2 -2x = 0 factors as x(x-2) = 0, and the solutions are x=0 and x=2.
I’m intentionally trying not to give direct hints too soon, because this is a very valuable lesson to learn; as I indicated, I was almost fooled, so it is rather subtle. But it happens a lot, and I want you to have a big “aha” moment you won’t forget.
In checking for parallel lines, checking the slopes won’t catch a case where they don’t have slopes (vertical lines); that is the most direct hint I gave here. The second example illustrates how a solution can be missed because of an unstated assumption (that what you divide by is not zero).
Finding the answer by an imperfect method
Brine wrote back:
Oh ok I understand you. Is this the answer? 3?
This time Brine has cross-multiplied without first canceling: $$\frac{6-2x}{3-x}=\frac{x^2-1}{x^2}\\(6-2x)(x^2)=(x^2-1)(3-x)\\6x^2-2x^3=3x^2-x^3-3+x\\-x^3+3x^2-x+3=0$$ and then solved the cubic equation by factoring (by grouping). This gave two solutions: the imaginary solutions \(x=\pm i\) we saw before, and also \(x=3\). This work is better, but …
I answered,
Yes, that’s correct.
What you’ve done here is, I think, to cross-multiply your equation (6-2x)/(3-x) = (x2-1)/x2, and solve the resulting cubic. This amounts to factoring instead of dividing, as I recommended, though you started with a division (in writing the equation in the first place). Presumably you then checked that x = 3 worked.
Another way to think of it is to go ahead and do what you originally did, but then check whether canceling the x-3 factors eliminated a solution.
That is, one could just recognize that it was assumed that \(x-3\ne0\), and check to see if the opposite assumption produces a solution. Rather than avoiding the assumption, we would be making the assumption explicit, and taking the contrary assumption as a second case.
The equation doesn’t fully represent the problem
Unfortunately, that check would fail! He’s missed a more fundamental error:
But did you observe that, when you put x=3 into your initial equation, you get 0/0 = 8/9? So 3 is not actually a solution of that equation! (It would be called extraneous.) And it isn’t obvious that it is a solution of the actual problem, until you check it in the original problem. The real problem arises earlier than that: The equation doesn’t really represent the problem.
I generally tell students to check their answer, not by plugging it into their equation, but by checking if it works in the problem itself. When the equation is wrong, this will catch it. But here, the equation turns out to be wrong but our answer is correct!
So how do you check the solution? You have go back to the problem:
Let P(x,0), Q(3,x2), P1(2x,1), and Q1(6,x2). Find all possible values of x ∈ R such that PQ || P1Q1.
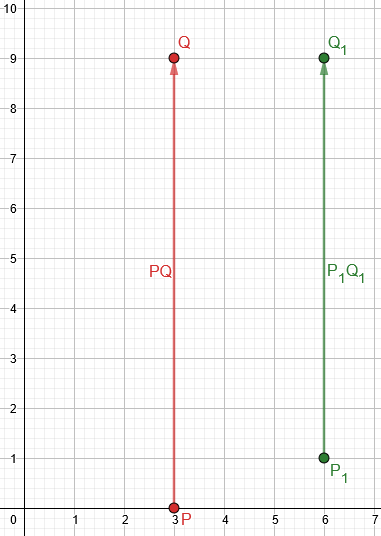
If x=3, the points are P(3,0), Q(3,9), P1(6,1), and Q1(6,9), and the vectors are PQ = <0,9>, P1Q1 = <0,8>. Are they parallel? Yes, because both are vertical — a case not covered by your equation! That is the ultimate cause of your difficulty.
This is what I’d found graphically (for \(x=3\)), which made me look again:
So, how can we solve the problem without making the unintentional assumption that the vectors are not vertical?
Back to square one: What really makes parallel vectors parallel?
What you never wrote, at the start, was what defines parallel vectors. I asked, “What fact are you using to justify the equation?”, and I’d still like an answer: What perspective were you taking on parallelism when you wrote that equation? What have you been taught about the meaning of “parallel”?
Two vectors are parallel if one is a scalar multiple of the other. In two dimensions, <a,b> and <c,d> are parallel if there is a non-zero scalar k such that <c,d> = k<a,b>; i.e. c = ka and d = kb. You have translated this to c/a = d/b = k; but that assumes that a and b are both non-zero. If you use this form, you need to separately check the contrary case.
Equivalently, one could take vectors to be parallel if their direction angles are the same, and then compare the tangents of those angles (their slopes): b/a = d/c. But those don’t exist for vertical vectors. If you do that, you need to separately consider the latter possibility.
His proportion was $$\frac{6-2x}{3-x}=\frac{x^2-1}{x^2}.$$
So, using his form, my “c/a = d/b”, you need to ask what happens when a denominator is zero, namely \(3-x=0\) or \(x^2=0\). The former leads to our missing solution.
If you used the “b/a=d/c” form, representing equal slopes, $$\frac{x^2}{3-x}=\frac{x^2-1}{6-2x},$$
you’d need to check when these denominators are zero, and in this case both are zero for \(x=3\) (that is, both vectors are vertical).
So if I were doing this carefully, I would not have started with the equality of two fractions, but with the definition using scalar multiplication:
PQ = <3-x,x2>
P1Q1 = <6-2x,x2-1>
These are parallel if P1Q1 = kPQ, so that
6-2x = k(3-x)
x2-1 = kx2
From the first equation, either k = (6-2x)/(3-x) = 2, or x = 3.
If k = 2, the second equation implies that x2 = -1, which is impossible.
If x = 3, then PQ = <0,9> and P1Q1 = <0,8>, and these are indeed parallel, with k = 8/9.
The solution of that first equation would look like this, done carefully: $$6-2x = k(3-x)\\2(3-x)-k(3-x)=0\\(2-k)(3-x)=0\\k=2\text{ or }x=3$$
Or I might eliminate k from the equations by writing your rational equation, while keeping in mind that in dividing by x2 and by x-3, I was assuming both are non-zero, and check those cases.
If we check the case \(x^2=0\), we find that \(\overrightarrow{PQ}=\left\langle3,0\right\rangle-\left\langle 0,0\right\rangle=\left\langle3,0\right\rangle\) and \(\overrightarrow{P_1Q_1}=\left\langle 6,0\right\rangle-\left\langle0,1\right\rangle=\left\langle6,-1\right\rangle\). These are not parallel.
Merely recognizing that your equation does not allow x = 3, and checking that separately, would also be valid, though it’s better to understand why. Just solving without canceling, as you have now done, is less appropriate, but it does lead to the answer (as long as you check it).
This is a very interesting problem, isn’t it?
Brine closed it out:
Yes you are right. I was actually taught that parallel vectors are parallel if they have a k value such that a=kb (where a and b are vectors) I forgot to apply this rule because in grade 12 I was taught by equaling the two slopes if they are parallel. I did learn the other method in the previous grade too but I forgot and I do remember it. The way you showed is way better that the one I did. Thank you so much for teaching me Dr. Peterson!
Sometimes we learn a shortcut method, or transfer it from one topic to another, and neglect to pay attention to conditions that are attached to them. It’s a good lesson!