Fundamental Theorem of Calculus: a Tale of Two Parts

(A new question of the week)

A recent question about the application of the Fundamental Theorem of Calculus provided an opportunity to clarify what the theorem means in practice, and specifically how the two parts are and are not related. Misunderstandings like these are probably more common than many instructors realize! We’ll also glance at some differences among textbooks that can have a bearing on the problem.

Do the two parts disagree?

Here is the question, from Alexander in early October:

Hello!

I have a question regarding The Fundamental Theorem of Calculus.

It says:

Part 1:

Let f be continuous and defined in the closed interval [a, b], and let F(x) = ∫_a^x f(t)dt, then F'(x) = f(x).

And also:

Part 2:

Let f be continuous and defined in the closed interval [a, b], and let F'(x) = f(x), then ∫_a^b f(x)dx = F(b) – F(a).

However, I do not understand why ∫_a^x f(t)dt = F(x), when (according to part 2) it should be equal to F(x) – F(a).

Let’s pause in the middle of the question to think about what he is saying.

The FTC is commonly stated either as two theorems, or as two parts of one theorem (occasionally given in the reverse order). Here, for example, is how it is presented in OpenStax calculus, which looks much like Alex’s:

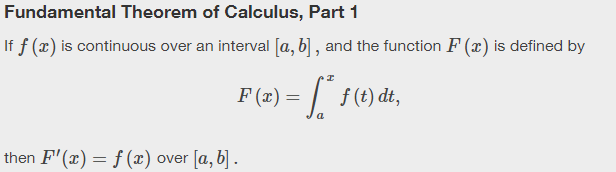
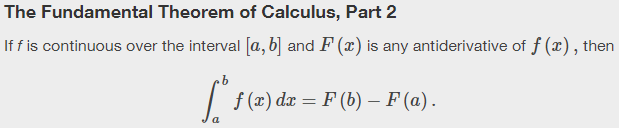
If we replace b with x in Part 2, $$\int_a^b f(x) dx=F(b)-F(a)$$ becomes $$\int_a^x f(x) dx=F(x)-F(a),$$ which seems to conflict with Part 1’s $$\int_a^x f(t) dt=F(x).$$ If you see through this immediately, good – but take a moment to see it through the eyes of a student new to all this, and ponder exactly why it is not a real issue!

A piecewise example

Alexander continued with a specific problem in which he got confused:

I will show an example of what I mean:

Problem:

Let f be a piecewise function defined by

f(t) = cos²(t) when 0 ≤ t ≤ 1

f(t) = t² + 1 when t > 1

Find for each x≥0 the integral ∫₀^x f(t)dt.

Solution:

First, I calculate the integral ∫₀¹ cos²t dt, which can be re-written as

∫₀¹ (1+cos(2t))/2 dt = [t/2 + sin(2t)/4]₀¹ = 1/2 + sin(2)/4.

Then I calculate ∫₁^x f(t) dt = ∫₁^x t² + 1 dt.

Here is where I encounter a problem. According to part 1 of the fundamental theorem of calculus,

F(x) = ∫₁^x t² + 1 dt = x³/3 + x.

However, according to part 2 of the theorem,

∫₁^x t² + 1 dt = F(x) – F(1) = x³/3 + x – 1/3 – 1.

The answer says the second option is the correct one, which makes me confused. I can understand why, but I find it hard to know when the first part of the fundamental theorem of calculus applies.

I understand why F'(x) = f(x), since d⁄dx (F(x) – F(a)) = F'(x) because F(a) is a constant. But the fact that F(x) in some cases equals F(b) – F(a), and in other cases equals F(x) confuses me, and I would be grateful if you could give me some insight.

Also, the “x” in “F(x)”, does it refer to the x in the upper limit of the integral, or is it just a dummy variable? Lets say I have the integral ∫₁^u f(t)dt, where u equals a function g(x). Is this integral equal to F(x) = F(u) – F(1), or is it equal to F(u)?

When do you use each part? That is, indeed, the issue.

The crux of the matter

Doctor Fenton answered, pointing out the significant, but subtle, difference between the parts:

Hi Alex,

The statements of Part 1 and Part 2 are two independent statements, not directly related to each other. In particular, the function denoted F(x) can be a different function in each part, even though the same symbol is used in both parts.

This is important: Each part has different premises, and is to be applied in a different situation; they are not used in parallel, with reference to the same function. In fact, though it is not obvious on the surface, they are opposites.

Here is how Stewart presents the theorem:

Note that Stewart uses g in the first part and F in the second, making them look less similar; that is probably intentional, and shows wisdom!

What Part 1 means

In Part 1, F(x) is DEFINED to be the function F(x) = ∫_a^x f(t)dt. If you change the lower limit from a to some other value b, you will have a different function F(x). For example, if f(x) = x and if a = 0, you have the function

F(x) = ∫₀^x t dt = x²/2 – 0²/2 = x²/2 ,

while if b=1, then the function G(x) = ∫₁^x t dt is

G(x) = ∫₁^x t dt = x²/2 – 1²/2 = x²/2 -1/2 .

Note that both F'(x) and G'(x) are f(x) = x.

The point is that if a function F(x) is defined by a definite integral of a continuous function f(t) with a variable upper limit of integration x, then no matter what the value of the lower limit of integration (as long as it is constant, and the definite integral is defined), the derivative of this function at a certain value x is just the value of the integrand (the function being integrated) at this same point x.

So here we are starting with a function f, and defining a new function F as its integral from some fixed lower limit a to a variable upper limit x. In the example, if we take \(f(x) = x\) and define $$F(x)=\int_a^x f(t)dt =\int_a^x t dt = \frac{x^2}{2}- \frac{a^2}{2}$$ then we find that $$\frac{d}{dx}F(x) =\frac{d}{dx} \left(\frac{x^2}{2}- \frac{a^2}{2}\right)= x$$ regardless of the value of the constant a.

This theorem tells us that this will always be true, for any suitable function f.

(Note, by the way, that he used Part 2 (also called the evaluation theorem) to evaluate the integral; but that integral could instead be evaluated by actually taking a limit of Riemann sums, so the example of Part 1 doesn’t depend on Part 2.)

Another way to present this part (quoted from Briggs, a calculus text used at my school) is:

If f is continuous on \([a,b]\), then the area function $$A(x)=\int_a^x f(t) dt\text{,  for }a\le x\le b,$$ is continuous on \([a,b]\) and differentiable on \((a,b)\). The area function satisfies $$A'(x)=f(x).$$ Equivalently, $$A'(x)=\frac{d}{dx}\int_a^x f(t) dt=f(x),$$ which means that the area function of f is an antiderivative of f on \([a,b]\).

Here we have both a different name for the function, and a different way to show the result as the derivative of an integral. In this form we can clearly see that the (definite) integral and derivative are “inverses” in that the derivative “undoes” the integral.

What Part 2 means

What about Part 2? Here is how Briggs states it:

If f is continuous on \([a,b]\) and F is any antiderivative of f on \([a,b]\), then $$\int_a^b f(x) dx=F(b)-F(a).$$

Mimicking the alternative form of Part 1, since f is the derivative of F, we could write this as $$\int_a^b \frac{d}{dx}F(x) dx=F(b)-F(a).$$ So Part 2 shows that the integral undoes the derivative (in a particular way).

Doctor Fenton continues:

In Part 2, F(x) is not defined as this integral, but only as a function F(x) whose derivative F'(x) is f(x). You should know from your study of derivatives that if two functions F(x) and G(x) have the same derivative for all x in the common domain, F'(x) = G'(x), then there is a constant C such that G(x) = F(x) + C. So, if we know that F'(x) = f(x), then for any limits of integration a and b such that the integral ∫_a^b f(t) dt is defined,

∫_a^b f(t) dt = F(b) – F(a) .

Since we also know that G'(x) = f(x), then Part 2 also tells us that

∫_a^b f(t) dt = G(b) – G(a) .

Then since the left side of both equalities is the same, then

F(b) – F(a) = G(b) – G(a), or F(b) = G(b) – G(a) + F(a).

That is, for any admissible value of the upper limit b,

F(b) = G(b) + a constant C, where C = F(a) – G(a).

Thinking of b as a variable and denoting it by x, this says F(x) = G(x) + (F(a) – G(a)).

This time, rather than starting with f and defining a new function (F, or g, or A) as an integral, we either start from F and obtain f as its derivative, or start from f and (somehow) find an antiderivative F; either way, we start knowing that \(F’=f\) (which in Part 1 was the conclusion). Since there are many antiderivatives for a function, we need the subtraction, which counteracts the effect of the constant of integration.

How do we solve his problem?

Recall that the problem he was working was this:

Let f be a piecewise function defined by

$$f(t)=\left\{\begin{matrix}\cos^2(t))&\text{when }0\le t\le1\\t^2+1&\text{when }t>1\end{matrix}\right.$$

Find for each \(x\ge0\) the integral \(\displaystyle\int_0^x f(t)dt\).

The required integral looks like Part 1; but is it?

Here is a graph of the piecewise-defined function f:

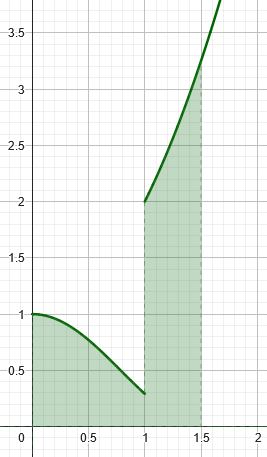
I have shaded the area from \(x=0\) to \(x=1.5\), which will give the value of the requested integral for \(x=1.5\).

Note, incidentally, that both parts of the theorem, as given to us in all our sources, require f to be a continuous function, but this is not! The work will have to apply the theorem separately to each piece of the function. But we’ll see that the resulting function is in fact continuous (though not differentiable at \(x=1\)); and in fact Part 2 is valid even for a discontinuous function like this, as long as it is integrable. The area between two values of x will be the difference in the antiderivative we’ll be finding.

Now we can look at Alexander’s questions on the problem:

In your examples

First, I calculate the integral ∫₀¹ cos²t dt, which can be re-written as ∫₀¹ (1+cos(2t))/2 dt = [t/2 + sin(2t)/4]₀¹ = 1/2 + sin(2)/4.

That is correct.

Then I calculate ∫₁^x f(t) dt = ∫₁^x t² + 1 dt.

This is correct only if x > 1. If x < 1, you need to use the other formula for f(t), and the fact that ∫_a^b f(t)dt = -∫_b^a f(t)dt .

However,

∫₁^x t²+1 dt =∫₁^x t²dt + ∫₁^x 1 dt = (x³/3 – 1³/3) + (x – 1) = x³/3 + x – 4/3 .

But this is not what Part 1 is about. Part 1 is about the derivative of a function defined by a definite integral with the variable being the upper limit of integration. Since you computed F(x) (which is not what Part 1 is about, so you are actually using part 2 in this step, with b=x), you can now differentiate x³/3 + x – 4/3 and get x²+1, which is exactly what Part 1 says you will get.

Does this help with your confusion?

Alexander is apparently assuming \(x\ge 1\) in his work; for \(x\le1\), the integral will just be $$\int_0^x\cos^2(t)dt=\left.\frac{t}{2}+\frac{\sin(2t)}{4}\right|_0^x=\frac{x}{2}+\frac{\sin(2x)}{4}$$

Then for \(x>1\), we have $$\int_0^x f(t)dt=\int_0^1 \cos^2(t)dt+\int_1^x t^2+1dt\\=\frac{1}{2}+\frac{\sin(2)}{4}+\frac{x^3}{3}+x-\frac{4}{3}\\=\frac{x^3}{3}+x+\frac{\sin(2)}{4}-\frac{5}{6}$$

So the full answer to the problem is

$$f(t)=\left\{\begin{matrix}\frac{x}{2}+\frac{\sin(2x)}{4}&\text{when }0\le t\le1\\\frac{x^3}{3}+x+\frac{\sin(2)}{4}-\frac{5}{6}&\text{when }t>1\end{matrix}\right.$$

This work involved repeatedly finding antiderivatives of the given functions, and applying Part 2 to evaluate the integrals. To apply Part 1, we would need to have a function already defined as an integral, such as the answer we found! Then we would conclude that this new function is an antiderivative. In fact …

Here (in red) is a graph of the integral:

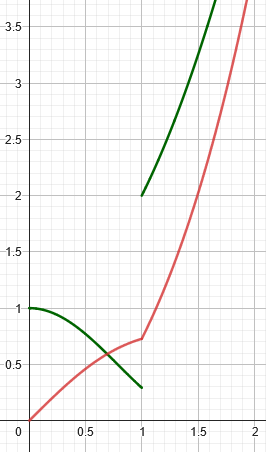
If you observe carefully, you can see that the slope of the red curve at any point is equal to the value on the green curve, which is what Part 1 says. That slope changes abruptly when the green function jumps: it is not differentiable there, so in fact this is not fully an antiderivative, because the condition of Part 1 is not satisfied.

The role of the variables

You also write

Also, the “x” in “F(x)”, does it refer to the x in the upper limit of the integral, or is it just a dummy variable? Lets say I have the integral ∫₁^u f(t)dt, where u equals a function g(x). Is this integral equal to F(x) = F(u) – F(1), or is it equal to F(u)?

The x in F(x) and the upper limit of integration are the same. If F(u) = ∫₁^u f(t) dt, and if u is a function of x, u=g(x), then

F(u) = F(g(x)) = ∫₁^g(x) f(t)dt,

so to differentiate d/dx F(x), you must use the Chain Rule:

d/dx F(g(x)) = dF/du * du/dx = f(u) * g'(x) = f(g(x)) g'(x).

(dF/du = f(u) by Part 1).

Let’s take a simple example. Suppose \(f(x)=3x^2\), and \(g(x)=\sin(x)\). Then if we define a function

$$H(x)=\int_1^{g(x)}f(x)dx=\int_1^{\sin(x)}3x^2dx,$$

then its derivative is (by Part 1)

$$H'(x)=\frac{d}{dx}\int_1^{\sin(x)}3x^2dx=f(g(x))g'(x)=3(\sin(x))^2\cdot\cos(x)=3\sin^2(x)\cos(x)$$

To check this, we can carry out the integration (using Part 2):

$$H(x)=\int_1^{\sin(x)}3x^2dx=\left[x^3\right]_1^{\sin(x)}=\sin^3(x)-\sin^3(1),$$

and the derivative is (by the chain rule):

$$H'(x)=\frac{d}{dx}\left(\sin^3(x)-\sin^3(1)\right)=3\sin^2(x)\cos(x),$$

which is just what we expect.