(A new question of the week)
Riemann sums are used in defining the definite integral. But they can also be used in reverse: Sometimes you can be given the limit of a summation and asked to read it as a Riemann sum, and then turn it into an integral. Usually this is fairly straightforward; but it can be trickier, as we will see here.
Seeing a sum as a Riemann sum
First, I want to start with a typical problem, before turning to the trickier problem from our “patient”. Not finding any questions of this sort in the Ask Dr. Math archive, I’ll pick one I found online:
Rewrite the limit of the Riemann sum as a definite integral:
$$\lim_{n\to\infty}\sum_{i=1}^n\left(5+\frac{3i}{n}\right)^5\frac{3}{n}$$
A Riemann integral, as stated on that site, has the form $$\int_a^bf(x)dx=\lim_{n\to\infty}\sum_{i=1}^nf(x_i)\Delta x,$$ where $$\Delta x=\frac{b-a}{n}$$ is the width of each rectangle, and $$x_i=a+i\Delta x,$$ so that \(x_0=a\) and we add \(\Delta x\) each time, ending with \(x_n=a+n\frac{b-a}{n}=b\).
So we need to match up parts of the given sum with parts of the Riemann sum, to find \(f(x)\), \(\Delta x\), and the limits of integration.
It looks like the function will be \(\left(5+\frac{3i}{n}\right)^5\). If we take \(x_i=5+\frac{3i}{n}\), then we find that \(a=5\) and \(\Delta x=\frac{3}{n}\), so \(b-a=3\) and \(b=8\). Conveniently, the function is multiplied by exactly \(\Delta x\). (We could have had to insert an extra constant multiplier.)
So our sum becomes $$\lim_{n\to\infty}\sum_{i=1}^n\left({\color{Red}{5+\frac{3i}{n}}}\right)^5{\color{Green}{\frac{3}{n}}}=\lim_{n\to\infty}\sum_{i=1}^nf({\color{Red}{x_i}}){\color{Green}{\Delta x}}=\int_a^bf({\color{Red}{x}}){\color{Green}{dx}}=\int_5^8{\color{Red}{x}}^5{\color{Green}{dx}}$$
The source I got this from focuses on \(\Delta x\) rather than \(x_i\), and makes the arbitrary choice \(a=0\) and \(b=3\), resulting in the answer $$\int_0^3(5+x)^5dx$$ This illustrates the fact that the answer is not necessarily unique. But the value of the integral will be the same either way; you may notice that a “u-substitution” will change one to the other. Both have the value $$\int_5^8x^5dx=\left[\frac{1}{6}x^6\right]_5^8=\frac{1}{6}8^6-\frac{1}{6}5^6=41,086.5$$
(Just for fun, I used a spreadsheet to sum this series for \(n=100\) and got 41,532.45; because it is a right Riemann sum of an increasing function, the sum is always greater than the integral, and takes a long time to converge.)
Most examples I find are similar to this, designed carefully to match the standard pattern. But then, sometimes, things are a little different …
A sum with a twist
Here is the question we got from Alexander, in mid-October:
The question:
Express the given limit as a definite integral:
lim n→∞ Σni=1 (1/n) arctan ((2i-1)/2n)
How I tried to solve it:
I want to write this as ∫ab f(xi)dx.
I see that the length of each sub-interval is 1/n (although I do not know how I could prove this mathematically, so I would appreciate help with that as well. Has it something to do with putting in i = 1, 2, 3, … , n-1, n in ((2i-1)/2n), in which case I get 1/2n, 3/2n, 5/2n, and each interval is 2/2n = 1/n?).
I have the points x0, x1, x2, … , xi-1, xi, … , xn-1, xn and the distance between each point is 1/n.
Thus, if x0 = 0, I can write these points as following:
0, 1/n, 2/n, … , (i-1)/n, i/n, … , (n-1)/n, n/n = 1.
From this I now know that a and b in the limits of the integrals equal 0 and 1. Additionally, I know that xi=i/n.
Now I only need to find f(xi) and I am done.
Here is where I encounter problems. Firstly, how do I know what I should put as f(x)? In this case, I guess it is arctan, but how do I know it?
Since ((2i-1)/2n) = (i/n) – (1/2n) = xi – 1/2n, I say f(x) = arctan (xi – 1/2n). However, if I am not mistaken, I want to find f(xi), not f(xi-1/2n). When I say f(xi) I refer to the height of the rectangle in the interval [xi-1, xi]. Is the height equal to xi – 1/2n, but what is xi then? I believe this is where I get confused, and I would be grateful if you could help me. The answer is: ∫01arctan(x)dx.
Also, if I have ((2i-1)/2n) and put in i = 1, 2, 3, …, I get that the end point (where i = n) is (2n-1)/2n which, for me, is hard to draw any conclusions from. Why does this answer differ from my previous answer where the endpoint xn = n/n = 1?
He is given $$\lim_{n\to\infty}\sum_{i=1}^n\frac{1}{n}\arctan\frac{2i-1}{2n}$$ and wants to write it in the form $$\lim_{n\to\infty}\sum_{i=1}^nf(x_i)\Delta x=\int_a^bf(x)dx$$ On the whole, the work is excellent.
No need to prove your choice
I answered:
Hi, Alexander.
You ask some good questions!
You’ve done some good thinking, and are not far from the answer. I am a little curious about the reason the problem is, as you note, a little different from others you have done; but I suspect it may be meant intentionally to call your attention to some important details about the definition of the Riemann integral that may be missed when the examples are too much alike. So this will be a good thing to discuss.
You say,
I see that the length of each sub-interval is 1/n (although I do not know how I could prove this mathematically, so I would appreciate help with that as well. Has it something to do with putting in i = 1, 2, 3, …, n-1, n in ((2i-1)/2n), in which case I get 1/2n, 3/2n, 5/2n, and each interval is 2/2n = 1/n?).
I have the points x0, x1, x2, … , xi-1, xi, … , xn-1, xn and the distance between each point is 1/n.
Thus, if x0 = 0, I can write these points as following:
0, 1/n, 2/n, … , (i-1)/n, i/n, … , (n-1)/n, n/n = 1.
From this I now know that a and b in the limits of the integrals equal 0 and 1. Additionally, I know that xi = i/n.
The first point I want to make is that, since we are essentially working backward to make a given sum take the form of a Riemann sum, there will not necessarily be only one possible answer (though the final answer, the value of the integral, will be unique); so it may not be possible to prove that your choices are the only ones possible. When I see a problem like this, I think of it not as finding the one way to do it, but as a case of trying things out and seeing if they work. If they do, fine. The proof is in the integral, you might say.
There is no claim that a series can be written as a Riemann series in only one way; in fact, if you think about it, we could use substitution to change the variable in many ways. Likely, though, there will be one “nicest” form, which would be the one you would happen to see. We only need to find an integral that can represent this series, not the “correct” one.
Thinking it through
So when you ask,
Firstly, how do I know what I should put as f(x)? In this case, I guess it is arctan, but how do I know it?
… maybe it would be possible to use a different function in the integral, such as arctan(2x) rather than arctan(x); but the latter seems natural, so that’s what we’ll use. Similarly, we don’t have to use the interval [0,1], but that seems natural. You don’t need to know; you just need to try it. If something didn’t work, we’d modify it.
There is nothing irrational about trying the obvious – as long as you don’t insist on it if things start to go wrong.
The presence of 1/n suggests strongly that we take Δx = 1/n, and the fact that the argument of arctan is (2i-1)/(2n), so that the difference between successive values is 2/(2n) = 1/n suggests that we use arctan(x) where x will vary from 0 to 1. These are the ideas you’ve expressed, and they are just what I would do.
At this point, everything seems to be fitting together, so we are encouraged. Until …
So we are led to write the integral ∫01arctan(x)dx, or something very much like it; but this doesn’t match your expectations, when you say:
Since ((2i-1)/2n) = (i/n) – (1/2n) = xi – 1/2n, I say f(x) = arctan (xi – 1/2n). However, if I am not mistaken, I want to find f(xi), not f(xi – 1/2n). When I say f(xi) I refer to the height of the rectangle in the interval [xi-1, xi]. Is the height equal to xi – 1/2n, but what is xi then?
First, we can think about whether this is really a problem. We’ll be taking a limit as n→∞, so that 1/(2n) will approach 0, and the value of x won’t be far off. Your problem isn’t too serious. But we do need to pay attention to details, and can’t just brush off the issue you see. What can we do?
Here is what we have so far, by taking \(\Delta x=\frac{1}{n}\), \(x_i=\frac{i}{n}\), and \(f=\arctan\):
$$\lim_{n\to\infty}\sum_{i=1}^n{\color{Green}{\frac{1}{n}}}{\color{Blue}\arctan}\left({\color{Red}{\frac{i}{n}-\frac{1}{2n}}}\right)=\\\lim_{n\to\infty}\sum_{i=1}^n{\color{Blue}\arctan}({\color{Red}{x_i-\frac{1}{2n}}}){\color{Green}{\Delta x}} = \int_0^1{\color{Blue}\arctan}({\color{Red}{x?}}){\color{Green}{dx}}$$
Close, but not quite!
Checking the definition
We need to look back at the definition of a Riemann sum. I’ve seen slightly different presentations, some not quite as careful as others; here is one from Wikipedia:
Note the asterisk. (Let me know if the definition you were given lacks this or some equivalent.) It’s saying that the argument of the function does not have to be xi itself; that would give us the right Riemann sum. The argument can be any point in the ith interval. This is where many problems of this type probably miss the generality of the definition, by sticking with right or left sums.
In the example I started with, we were given a formula that lacked the asterisks; it represented only the right Riemann sum. This seems to be common, unfortunately.
In general, though, the terms of the sum can be based on any random point in an interval; here is an example (for our function, stretched by a factor of 4 for visibility, with \(n=10\)) using an app that will be mentioned below:
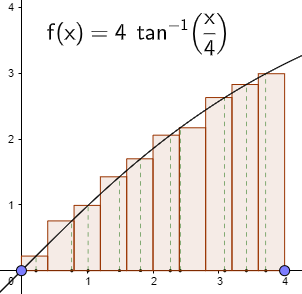
Notice how the heights vary irregularly; Alexander’s mention of “the height of the rectangle in the interval \([x_{i-1},x_i]\)” missed this point.
Here is what the right Riemann sum would look like for this function:
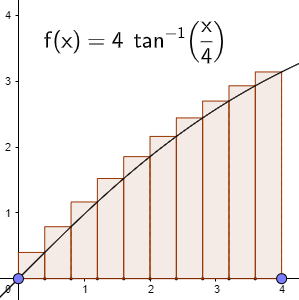
That’s what Alexander was expecting. But what does he actually have?
What the summation really is
So let’s just take the choices you’ve made, with xi = i/n. Our ith interval will be [xi-1, xi] = [(i-1)/n, i/n]. Our xi*, from the given summation, will be (2i-1)/(2n). Is that in this interval? Yes, because
(i-1)/n < (2i-1)/(2n) < i/n
is equivalent to
2(i-1) < 2i-1 < 2i
(multiplying by 2n), which is true. (In fact, it’s exactly in the middle, so it turns out this is the midpoint Riemann sum, rather than the right sum as you were expecting.)
To see easily that our expression is the midpoint of an interval, observe: $$\frac{2i-1}{2n}=\frac{i}{n}-\frac{1}{2n}=x_i-\frac{1}{2}\Delta x$$
Here is the midpoint Riemann sum:
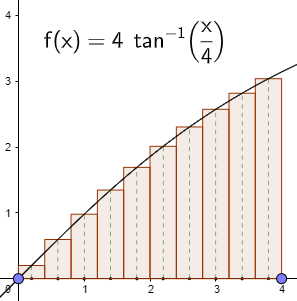
That’s what our sum represents. But the limit is the same either way.
So we can rewrite the given summation as
Σni=1 (1/n) arctan((2i-1)/(2n)) = Σni=1 arctan(xi*) Δx
which is a Riemann sum, and its limit is
∫01arctan(x) dx
So, as I suggested, we just had to take your natural suppositions, try them out, and see that they work out. Your only error, if we can call it that, is in assuming xi and xi* have to be the same thing, and therefore thinking you were wrong.
And it’s worth noting that they could have put other similar expressions into the argument of the arctan, and we’d get the same limit. The limit process irons out all sorts of little variations.
So now, taking $${\color{Green}{\Delta x}}={\color{Green}{\frac{1}{n}}},\\ {\color{Red}{x_i^*}}=x_i-\frac{1}{2}\Delta x={\color{Red}{\frac{2i-1}{2n}}},\\ {\color{Blue}f}={\color{Blue}{\arctan}},$$ we have
$$\lim_{n\to\infty}\sum_{i=1}^n{\color{Green}{\frac{1}{n}}}{\color{Blue}\arctan}\left({\color{Red}{\frac{2i-1}{2n}}}\right)=\\\lim_{n\to\infty}\sum_{i=1}^n{\color{Blue}\arctan}({\color{Red}{x_i^*}}){\color{Green}{\Delta x}} = \int_0^1{\color{Blue}\arctan}({\color{Red}{x}}){\color{Green}{dx}}$$
By the way, in looking for definitions, I found this textbook section that nicely shows the effect of varying xi*, including an app to play with that includes a random value option; the next section defines the Riemann integral as the limit. I’ll be interested to hear whether your instructor explains some or all of this.
We didn’t hear back, but I have a little more to say.
I observe that as a midpoint Riemann sum, this series should be a very good approximation of the integral, even for relatively small n. The integral, without showing details (I looked it up in an integral table), turns out to be $$\int_0^1\arctan(x)dx=\left[x\arctan(x)-\frac{1}{2}\ln(1+x^2)\right]_0^1=\frac{\pi}{4}-\frac{\ln(2)}{2}\approx0.438825,$$ while the sum for \(n=5\) is $$0.019934+0.058291+0.092730+0.122145+0.146563=0.439663,$$ which is pretty good. You can imagine how close it is for \(n=100\)!
Two more examples: basic and extreme
In searching for past questions and answers on this topic, although I found no answers to similar questions to share, there have been a couple questions, both from last year, about this kind of problem. (They didn’t lead to publishable discussions because in one case the student was trying a problem that was beyond him – he knew nothing of integration – and in the other, they never responded to a hint.)
The first is a simple one at the level of the first example above:
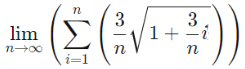
Here I would let \(x_i=1+\frac{3}{n}i\), so that \(a=1\) and \(\Delta x=\frac{3}{n}\), to get a right Riemann sum. But you could also just let \(x_i=\frac{i}{n}\), leading to a different interval, and even a different \(\Delta x\).
The second is considerably more complicated:
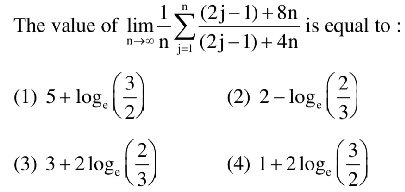
This one hardly looks like a Riemann sum at all! We’ll have to rewrite it considerably to make it match up; in particular, we’d like to see something containing \(\frac{j}{n}\), ideally only once, but possibly in several places (as the argument to a more complicated function), in order to recognize what \(x_j^*\) is. My first inclination is to start by simplifying the big fraction by changing it from an improper fraction to a mixed fraction:
$$\frac{(2j-1)+8n}{(2j-1)+4n}=\frac{[(2j-1)+4n]+4n}{(2j-1)+4n}=1+\frac{4n}{(2j-1)+4n}$$
Now j appears only once. To get it to appear in the form \(\frac{j}{n}\), we can divide numerator and denominator by n:
$$\dots=1+\frac{4}{\frac{2j-1}{n}+4}$$
This is almost good, except that \(\frac{2j-1}{n}\) would be an odd multiple of \(\Delta x=\frac{1}{n}\), and we would not have all \(x_i\). So something is not as we expect …
Let’s go back and divide, not just by \(n\), but by \(4n\):
$$\dots=1+\frac{1}{\frac{2j-1}{4n}+1}=1+\frac{1}{1+\frac{j-\frac{1}{2}}{2n}}$$
What happens if we let $$x_j^*=1+\frac{j-\frac{1}{2}}{2n}?$$ This suggests \(a=1\) and \(\Delta x=\frac{1}{2n}\), so that \(b=a+n\Delta x=1+n\frac{1}{2n}=\frac{3}{2}\). Then if $$x_j=a+j\Delta x,$$ $$x_j^*=1+\left(j-\frac{1}{2}\right)\Delta x$$
That \(j-\frac{1}{2}\) makes it clear that this \(x_j^*\) is midway between \(x_{j-1}\) and \(x_j\). So this is another midpoint Riemann sum!
So our sum has become $$\lim_{n\to\infty}\sum_{j=1}^n\left(1+\frac{1}{x_j^*}\right)\cdot 2\Delta x=\int_1^\frac{3}{2}2\left(1+\frac{1}{x}\right)dx=\\2\left[x+\ln(x)\right]_1^\frac{3}{2}=2\left[\frac{3}{2}+\ln(\frac{3}{2})\right]-2\left[1+\ln(1)\right]=\\3+2\ln\left(\frac{3}{2}\right)-2=1+2\ln\left(\frac{3}{2}\right)$$
which is option (4) in the problem.
Once again, the limit should converge relatively quickly, so let’s check. The claimed value is 1.81093; taking \(n=5\) the sum is \(0.390476+0.373913+0.36+0.348148+0.337931\approx1.810468\). That looks pretty good.

