In response to a recent request for information about implicit differentiation (hi, Brian!), let’s take a look at that topic. It happens to be distantly related to Friday’s topic, which was about implicitly defined curves. We’ll start with a thorough explanation, and then look at several specific examples, capping it off with a weird one.
Our first question is from 2001:
Implicit vs. Explicit Differentiation What is the exact definition of 'Implicit Differentiation'? I have a very hard time with math terms (please use layman's terms). What is 'Explicit Differentiation'? I don't even know what the words implicit and explicit mean! What is the difference between them? Which do you use when? Thank you for the help.
In everyday usage, “explicit” means something has been directly and clearly stated or shown (“I explicitly told you to clean your room!), while “implicit” means something has been implied indirectly. The mathematical meaning is similar.
Doctor Fenton answered:
Dear Meghan, Thanks for writing to Dr. Math. This is a good question, and it depends on remembering what we mean by a function. Recall that a function is a rule that assigns exactly one y-value to a given x. Another way of stating this is that a vertical line always intersects the graph of a function in only one point. A function defined in the form y = f(x) is said to be "explicitly" defined. That means that y = x^2 or y = sin(x) is explicitly defined.
Such a function definition explicitly tells you how to find y from a given value of x; you don’t have to figure it out by solving an equation.
Sometimes we have a graph given in a form that isn't, or perhaps can't be, solved for y. For example: x^2 + y^2 = 1 or y*e^y = x
Some we can write explicitly
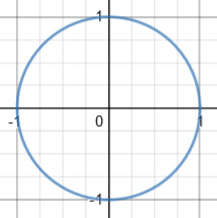
In the first case, you probably recognize the equation as the equation of a circle, centered at the origin, of radius 1. The whole graph is not a function because vertical lines between x = -1 and x = 1 hit the circle twice. In this example, we actually can solve for y: y^2 = 1 - x^2 so either y = + sqrt(1 - x^2) or y = - sqrt(1 - x^2) Both of these formulas define explicit functions: y = + sqrt(1 - x^2) is the upper half of the circle; and the other formula defines the lower half of the circle. Each semicircle IS the graph of a function, because vertical lines now hit the graph only once. We say that a function graph that is part of a larger graph (which may not be a function graph in its entirety) is "implicitly" defined by the larger graph or its formula.
Here is the graph of \(x^2+y^2=1\):
Here are the graphs of the two functions \(y=\sqrt{1-x^2}\) (green) and \(y=-\sqrt{1-x^2}\) (red):
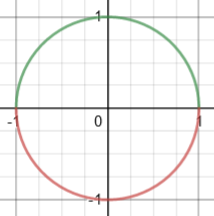
(Graphs here are made with Desmos, which does nicely with most implicit equations.)
Some we can’t
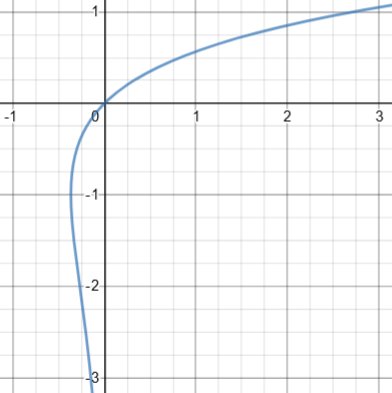
The second example gives a graph that IS a function graph, but there is just no way to rewrite it in the form y = f(x), so we say in this case, too, that y is "implicitly" defined by the equation (y*e^y = x in this case).
Here is a graph of \(ye^y=x\):
This, too, could be split into two functions, though we can’t write explicit equations for them:
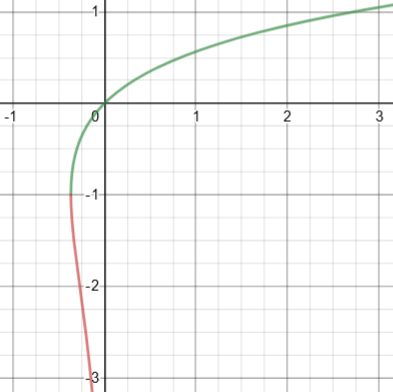
(This equation, on the other hand, does define x explicitly as a function of y; and we can differentiate that function explicitly. We’ll see equations below that lack this feature.)
Implicitly differentiating the circle
For implicit differentiation, we have a formula F(x,y) = 0 which we either can't or don't bother to solve for y. For example, the circle equation would be: x^2 + y^2 - 1 = 0 and the other equation would be: y*e^y - x = 0
Here we got 0 on one side just to match the general form \(F(x,y)=0\); that is not essential, and we won’t always do that here.
We can still compute derivatives, by using the Chain Rule whenever y occurs in the formula. In the circle example, the left side is a sum of three functions of x: x^2, y^2, and the constant 1. The derivative of a sum is the sum of the derivatives, so we differentiate with respect to x (which I will denote by an apostrophe, ') : (x^2)' + (y^2)' + (1)' = (0)' The first term is easy: (x^2)' = 2x The derivative of a constant is 0, so 2x + (y^2)' + 0 = 0
We usually use the apostrophe notation (read as “prime”) only on variables or function names (\(y’\) or \(f'(x)\)), but there is nothing wrong with using it more broadly, as here. It could have been written as $$\frac{d}{dx}x^2+\frac{d}{dx}y^2+\frac{d}{dx}1=\frac{d}{dx}0$$
And we can do this because if two functions are equal (the left side and the right), their derivatives are also equal.
Since we are thinking of y as being a function of x, even though we don't know its formula, we can use the Chain Rule:
d(y^2) d(y^2) dy
-------- = ------ * --
dx dy dx
= 2y * y' (where I am now writing y' for dy/dx)
The first term on the right is just 2y, because we are differentiating y^2 WITH RESPECT TO y, so our equation becomes:
2x + 2y*y' = 0
Using d/dx notation, we have $$2x+2y\frac{dy}{dx}+0=0$$ I find \(y’\) notation very convenient for this work.
What we ended up with is an equation in \(x\), \(y\), and \(y’\), which must be true at any point on the graph.
We now solve for y':
2y*y' = -2x
-2x
y' = ----
2y
-x
y' = ---
y
Notice that y occurs in the answer.
The presence of y is not a problem; in fact it is necessary in cases where y is not a function of x, so that there could be different values of y for the same x! The slope can’t depend only on x.
Remember how there were TWO functions defined by the circle equation:
y1 = + sqrt(1 - x^2)
and
y2 = - sqrt(1 - x^2)
We can differentiate these functions explicitly, and get
-x -x
y1' = ------------- and y2' = --------------
sqrt(1 - x^2) -sqrt(1 - x^2)
or
-x -x
y1' = -- and y2' = --
y1 y2
(Instead of canceling the - signs in the second derivative, I have left them in, to show that the single formula from implicit differentiation computes BOTH derivatives with one computation!)
Here we can see the two slopes at two points with the same x:
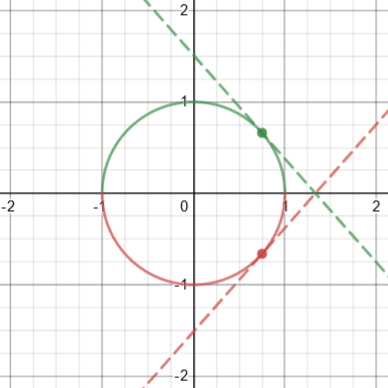
What about the other one?
For the second function, we would compute:
(y*e^y)' = (x)'
y'*(e^y) + y * (e^y)' = 1
(I used the Product Rule on the left)
y'*e^y + y*(e^y * y') = 1
(since by the Chain Rule,
d(e^y) d(e^y) dy
------ = ------ * -- = e^y * y' )
dx dy dx
Solving for y' gives
y' * (e^y + y*e^y) = 1
y' * e^y*(1 + y) = 1
1
y' = ---------
e^y*(1+y)
This answer again has the characteristic feature of implicit differentiation: y will appear in the answer.
Although we can’t solve for y, we can approximate the values. Here we see two points with the same x, and their tangents:
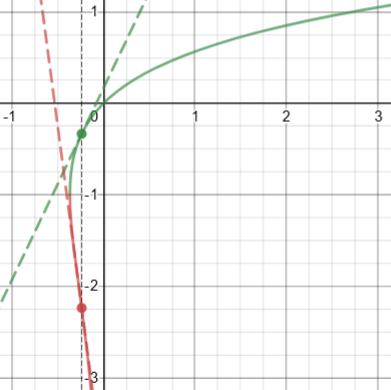
The green point is approximately \((-0.239, -0.333)\); the slope is $$\displaystyle y’=\frac{1}{e^y(1+y)}\approx\frac{1}{e^{-0.333}(1-0.333)}=2.09$$ The red point is approximately \((-0.239, -2.237)\); the slope is $$\displaystyle y’=\frac{1}{e^y(1+y)}\approx\frac{1}{e^{-2.237}(1-2.237)}=-7.57$$
And where is the tangent vertical? When the denominator, \(e^y(1+y)\), is zero, namely when \(y=-1\), and $$x=ye^y=(-1)e^{-1}\approx -0.368$$
Example 1: Radicals
We need more examples. We can start with one from 1996:
Implicit Differentiation How do I find dy/dx for: ((xy)^(1/2)) + ((x + 2y)^(1/2)) = 4
This can be written as $$\sqrt{xy}+\sqrt{x+2y}=4$$
Doctor Pete answered:
You wish to find dy/dx, that is, the rate of change in y as a function of x. Some functions aren't always expressible in the form y = f(x), as the above example shows. Rather, the best we can do is to write it as some f(x,y) = 0. But this doesn't mean that we can't find derivatives -- in the latter case, we see that the existence of f(x,y) means that x and y are related in some sense; changing x forces y to change as well. This is the idea behind implicit differentiation. If you understand the concept well enough, you should see that it is only a generalization of "regular" differentiation.
Again, though it can’t necessarily be solved for y, we assume that with some restrictions as we saw above, it can be turned into a function near a given point. (If it can’t, something will go wrong in the work.)
A similar example
Since the problem presented involved radicals, he demonstrated an example with a radical:
Here is an example: Find dy/dx if
f(x,y) = xy + x^2 - y^2 + Sqrt[x-y] = 0.
(Here, Sqrt[ ] is the square root function.) First find df(x,y)/dx; that is, take d/dx of the above (the right-hand side remains zero):
df(x,y) d
------- = ---- (xy + x^2 - y^2 + Sqrt[x-y])
dx dx
dy dy 1 1 dy
= x ---- + y + 2x - 2y ---- + --- --------- (1 - ----)
dx dx 2 Sqrt[x-y] dx
1 dy 1
= (x - 2y - -----------) ---- + 2x + y + ----------- = 0.
2 Sqrt[x-y] dx 2 Sqrt[x-y]
The product rule was needed for the first term, along with the chain rule; the last term was done by treating \(\sqrt{x-y}\) as \((x-y)^{1/2}\) and using the chain rule.
This was done by taking the derivative as usual, except when there was a y term, I wrote dy/dx. (Notice that d[y^2]/dx = 2y * dy/dx; this is actually from the chain rule.) The last step was simply collecting terms. So to find dy/dx, the rest is easy; simply move the terms without dy/dx to the other side, and divide by x - 2y - 1/(2 Sqrt[x-y]). The result is actually a new function g(x,y).
The derivative turns out to be $$y’=\frac{2x+y+\frac{1}{2\sqrt{x-y}}}{x-2y-\frac{1}{2\sqrt{x-y}}} = \frac{2(2x+y)\sqrt{x-y}+1}{2(x-2y)\sqrt{x-y}-1}$$
Here is the graph:
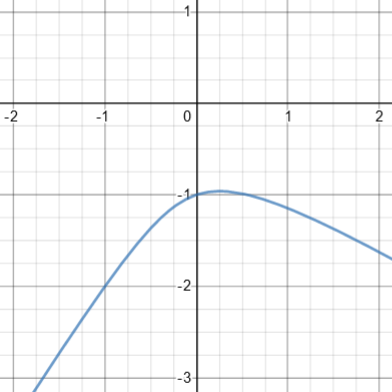
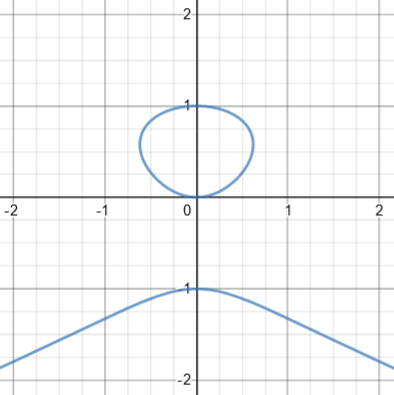
This time, y can be considered a function of x, though we can’t solve for it. Or is that true? If you examine the equation carefully, you see that (0, 0) also satisfies it; this would be an isolated point on the graph, which Desmos missed. Indeed, if you set \(x=0\) and solve to find the y-intercept(s), you find that \(y=0\text{ or }-1\); y is not a function of x! Here is the actual graph:
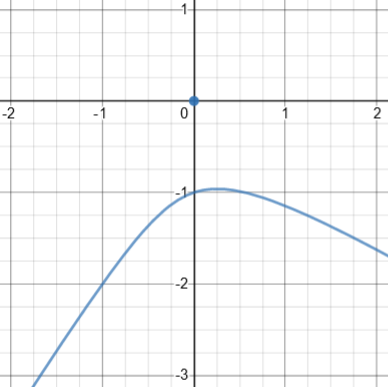
The requested problem
So I'll carry out the first few steps on your example, just to start you off:
d
---- (Sqrt[xy] + Sqrt[x+2y] - 4) = 0
dx
1 1 dy 1 1 dy
--- -------- ( x ---- + y ) + --- ---------- ( 1 + 2 ---- ) - 0 = 0
2 Sqrt[xy] dx 2 Sqrt[x+2y] dx
Now collect the dy/dx terms, move the other terms to the other side and solve for dy/dx.
Let’s carry that out: $$\frac{1}{2\sqrt{xy}}(xy’+y)+\frac{1}{2\sqrt{x+2y}}(1+2y’)=0\\ \frac{xy’}{2\sqrt{xy}}+\frac{y}{2\sqrt{xy}}+\frac{1}{2\sqrt{x+2y}}+\frac{2y’}{2\sqrt{x+2y}}=0\\ \left(\frac{x}{2\sqrt{xy}}+\frac{1}{\sqrt{x+2y}}\right)y’+\left(\frac{y}{2\sqrt{xy}}+\frac{1}{2\sqrt{x+2y}}\right)=0\\ y’=-\frac{\frac{y}{2\sqrt{xy}}+\frac{1}{2\sqrt{x+2y}}}{\frac{x}{2\sqrt{xy}}+\frac{1}{\sqrt{x+2y}}}=-\frac{y\sqrt{x+2y}+\sqrt{xy}}{x\sqrt{x+2y}+2\sqrt{xy}}$$
And here is a graph:
Example 2: A polynomial
Next, an example from 1998:
Differentiating Please help me differentiate (y^2) * cos (1/y) = 2x + 2y
Doctor Joe answered indirectly, as we prefer to do, solving a different problem:
Dear Stephen,
I shall not answer your question directly. I hope that you can do it yourself. What I shall do is to give you some advice while performing an example of this type of implicit differentiation.
Recall that if f is a function of y and y is also a function of x, then to differentiate f with respect to x, we need to apply the so-called chain-rule, right?
d d dy
-- f(y) = (-- f(y))* --
dx dy dx
which can also be written as:
df df dy
-- = -- * --
dx dy dx
For instance, differentiating y^3*sin(1/y^2) with respect to x gives:
{d/dy (y^3*sin(1/y^2))} * dy/dx
= {3y^2 * sin(1/y^2) + y^3 * cos(1/y^2) * (-2/y^3)} * dy/dx
That example of using the chain rule is meant to prepare Stephen for that part of his problem, which is harder than the example we’ll be doing.
Now we’ll do a simpler implicit differentiation:
In a more complicated example, the next thing you would do would be to group the terms that have a factor of dy/dx together. To show you another example: Differentiate with respect to x, x^2 + y^3 = y We start differentiating implicitly with respect to x: 2x + (3y^2 * dy/dx) = dy/dx => dy/dx * (3y^2 - 1) = -2x => dy/dx = 2x/(1-3y^2) After grouping the dy/dx terms together, we were able to isolate them on one side of the equation. Note that the final expression of dy/dx usually involves a quotient. In the last example that I gave, the denominator is (1-3y^2). Don't think that everything is fine. Sometimes you have to check to see whether your derivative makes sense at certain special points - in this case it is the value when y = sqrt(1/3) .
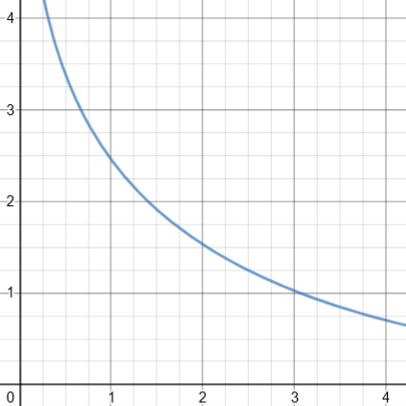
In this example (as in Stephen’s) it is possible to solve for x in terms of y: \(x=\pm\sqrt{y(1-y^2)}\). With some work, we can see that y can’t be greater than 1, or between \(-1\) and 0. And when we graph it, we see that those points where \(y=\sqrt{\frac{1}{3}}\approx 0.577\) are where the tangent is vertical, as we would expect:
(This is an algebraic curve like those we looked at Friday.)
Now you can solve the problem you posed using the same methods I illustrated in my examples. You will go through the following steps: 1) differentiate each term with respect to x (and use the chain-rule when a term has y's in it), 2) rearrange and group the terms to solve for dy/dx.
I won’t pursue the original problem, which was \(y^2 \cos\left(\frac{1}{y}\right) = 2x + 2y\), because it turns out that the graph is ugly and the derivative is not illuminating!
Example 3: Exponentials
Here is another question from 1998:
Implicit Differentiation I am a student who is very interested in calculus. I have some knowledge of how to differentiate functions in the form y = f(x). However, how do you differentiate an equation that cannot be expressed in terms of x or y? i.e. x + x^y = y^x I know this has to do with Implicit Differentiation, but I don't know how. Can you please help me?
Doctor Jerry answered:
Hi Roger, Assuming that the equation x + x^y = y^x can be solved for y in terms of x (this might require assumptions about allowable values of x), one thinks about y as a function of x and applies the chain rule. For example, if y is a function of x, then the derivative of x*y with respect to x is 1*y+x*y'. I just applied the product rule. Since I don't have y as an explicit function of x, I can only write y' for the derivative of y with respect to x.
If you think about it, this is the fundamental idea behind all of algebra: when you don’t know what something actually is, just write a symbol for it and keep going as if you did. (Of course, you don’t just pretend all the way, but at some point determine under what conditions it really does exist.)
After showing the example of the circle what we have already seen, he takes on the given problem:
For x + x^y = y^x, we have
x + e^(y*ln(x)) = e^(x*ln(y))
Differentiating,
1 + e^(y*ln(x))(y'*ln(x) + y/x) = e^(x*ln(y))(ln(y) + (x/y)y')
1 + x^y(y'*ln(x) + y/x) = y^x(ln(y) + x*y'/y)
You can now solve this expression for y' in terms of x and y. As you can see, the entire procedure rests on the chain rule.
Again, let’s carry out what Roger presumably did a couple decades ago:
$$1+e^{y\ln(x)}\left(y’\ln(x)+\frac{y}{x}\right)=e^{x\ln(y)}\left(\ln(y)+\frac{x}{y}y’\right)\\ 1+x^{y}\left(y’\ln(x)+\frac{y}{x}\right)=y^{x}\left(\ln(y)+\frac{xy’}{y}\right)\\ \left(x^{y}\ln(x)-y^{x}\frac{x}{y}\right)y’=y^{x}\ln(y)-x^{y}\frac{y}{x}-1\\ y’=\frac{y^{x}\ln(y)-x^{y}\frac{y}{x}-1}{x^{y}\ln(x)-y^{x}\frac{x}{y}}= \frac{xy^{x+1}\ln(y)-y^2x^{y}-1}{yx^{y+1}\ln(x)-x^2y^{x}}$$
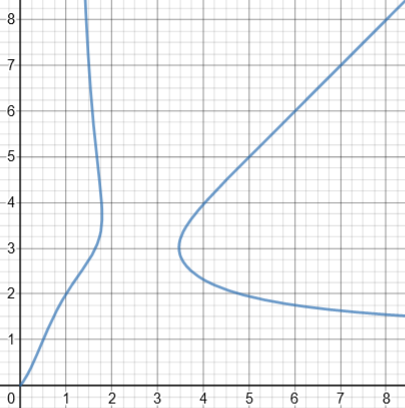
Here is the graph:
When things go wrong …
We’ll close with a problem showing one of the odd things that can happen. This is from 2001:
Implicit Differentiation We were given the equation 1 - xy = x - y. We found y' by implicit differentiation and got: y' = (1+y)/(1-x). However, if we solve the equation for y we get: y = -1 and so y' = 0. We have not been able to show that (1+y)/(1-x) = 0. We feel certain that solving for y first is a valid approach, but we're confused because we did not get the same value for y' both ways! Where have we gone wrong?
Let’s check that implicit differentiation: $$(1)’-(xy)’=(x)’-(y)’\\0-y-xy’=1-y’\\y’-xy’=1+y\\(1-x)y’=1+y\\y’=\frac{1+y}{1-x}$$
Looks good. I answered:
Hi, Gary. Actually, you haven't gone wrong; you just missed the last step. By implicit differentiation, you found that y' = (1+y)/(1-x). Then by solving the equation for y, you found that y = -1. That is, your equation is really just a horizontal line, and y' = 0. Now take your equation for y' and plug in y = -1. You get y' = 0, just as you wanted!
Recall that the formula we get for a derivative is only valid for \((x,y)\) that lie on the curve. So if we get two different formulas by different methods, they only need to agree for those pairs; they may be entirely different elsewhere. And having solved for y, we find that the derivative is really $$y’=\frac{1+y}{1-x}=\frac{1+-1}{1-x}=0$$ for all x.
But wait! There’s more!
Did you look at that last step and think, “But what if \(x=1\)?” If so, you are wise …
Actually, there's another dimension to this problem that you missed. When you solved for y, you really got
1-x
y = ---
x-1
which you then simplified by canceling x-1. But you can't do that if x = 1. A better solution would be
1 - xy = x - y
xy + x - y - 1 = 0
(x - 1)(y + 1) = 0
x = 1 OR
y = -1
So really your equation describes a pair of crossed lines, a horizontal line at y = -1 and a vertical line at x = 1. This has slope 0 on the former, and undefined slope on the latter. Note that y is nothing like a function of x, so solving for y doesn't accomplish everything you hoped for.
Now try plugging in x = 1 in your implicit derivative. Everything will work out just right.
I’ve mentioned before that when we solve an equation and find ourselves dividing by a quantity that could be zero, the better way is to factor, to avoid missing solutions. The same is true here. To check, if we replace x with 1 in the equation \(1 – xy = x – y\), we get \(1 – y = 1 – y\), which is true for all y; and if we replace y with \(-1\), we get \(1 + x = x + 1\), which is true for all x.
And when we set \(x=1\) in the derivative, we get \(\frac{1+y}{1-x}=\frac{1+y}{1-1}\) which is undefined, as expected for a vertical line.
We’ve seen a couple times when Desmos, which generally does a great job, missed something. Look at what it does for \(1 – xy = x – y\):
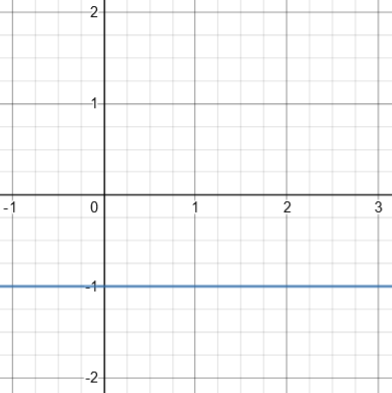
It made the same omission Gary did! As we’ve seen, the graph really looks like this:
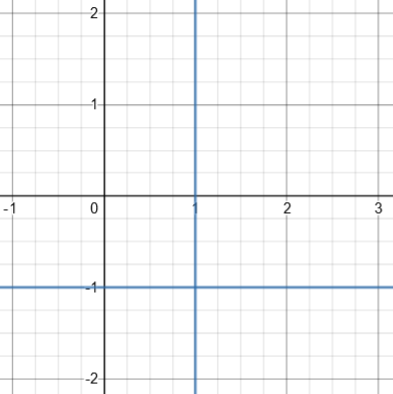
It's important to realize that when you take the derivative implicitly, it is assumed that x and y satisfy the original equation; when you plug in any pair that does, you will get the derivative at that point. Here, knowing only x = 1 or only y = -1 determines the point, and therefore the derivative. So your formula for the derivative did not have to equal 0 everywhere; it just had to be zero when y = -1, and undefined when x = 1, which is true.
So, what’s the bottom line? Implicit differentiation is not hard; but, as always, avoiding subtle errors requires careful attention. Don’t get complacent!

Pingback: A Surprising Route to a Differential Equation – The Math Doctors