(A new question of the week)
Some topics are hard to find information about at a basic level, because they are usually dealt with in advanced math courses, and yet the basic ideas can be understood without all the trappings. That is the case for the Affine Tangent Cone, which involves tangents to an algebraic curve, which are studied in Algebraic Geometry. I myself am not familiar with the topic, but we are fortunate to have a variety of Math Doctors who know math well enough to enjoy explaining it at whatever level is needed. I’ll be learning some things as I edit this! (And I get to play with some fascinating graphs.)
What is an affine tangent cone?
The question came from Andy in mid-January, who had been searching for accessible information about something he’d read:
Hello, I have a question about the number of tangents and affine tangent cone. Actually, someone said “If you draw the Affine Tangent Cone in the origin at the y2=x3+x2 then you can know that when there is singularity, you will intuitively understand why it is possible to figure out the number of tangents by considering from that point to the affine tangent cone.” So I wondered what number of tangents and affine tangent cone were related to. I drew picture of it, but I don’t know the relationship with the two elements.
We don’t know the context in which the subject arose; but some level of introduction was called for. What is an affine tangent cone, and how can it be used?
Algebraic curves
Doctor Jacques answered:
Hi Andy,
Given an algebraic curve f(x, y) = 0, if you want to investigate a possible singularity at the point (a, b) on the curve, it is easier to first move the point to the origin by replacing (x, y) with (x + a, y + b). We will assume that this has been done, and the point of interest is (0, 0), which is now on the curve.
Algebraic curves are defined, not, as we usually see in introductory algebra, as a function \(y=f(x)\), such as the polynomial function \(y=3x^3-2x-5\), but by a polynomial that may involve both variables on both sides, which can be rewritten with 0 on one side. Here are a couple examples of such curves that I found in MathWorld:
The bow curve, \(x^{4}=x^{2}y-y^{3}\), which crosses over itself, and has three tangents at the origin:
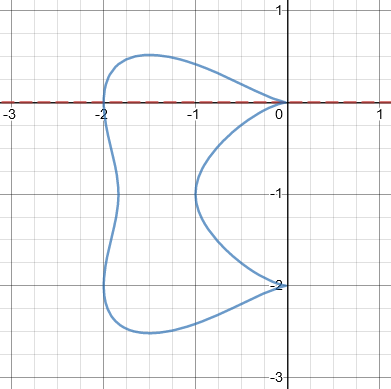
The bicuspid curve \(\left(x^2-1\right)\left(x-1\right)^2+\left(y^2-1\right)^2=0\), which has two “cusps”, or points: 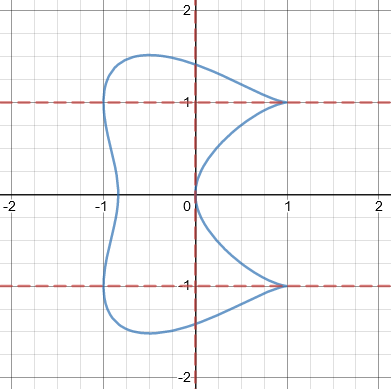
Here we see one tangent at the origin, and one at each of the cusps; to study the cusp at (1, 1), we would replace x with \(x+1\) and y with \(y+1\) to shift the graph left and down, to obtain \(\left(x+2\right)x^3+\left(y+2\right)^2y^2=0\):
Cusps and self-intersections are two kinds of “singularities”.
Finding the tangent cone
You should then separate f(x, y) into homogeneous components, i.e., rewrite the equation by collecting together the terms with the same total degree. Note that there will be no constant term, since (0, 0) is on the curve.
The affine tangent cone is then the homogeneous component with the lowest degree. If this has degree 1, it is simply the equation of the tangent at (0, 0), and the point is not singular.
A homogeneous polynomial is one in which the (total) degree of each term (the sum of the exponents) is the same, such as \(3x^2y-2xy^2+5y^3\), where each term has degree 3. For example, if we were given the equation \(x^3+3x^2-2xy^2-5x+y^2+7y=0\), collecting homogeneous components would yield \([x^3-2xy^2]+[3x^2+y^2]+[-5x+7y]=0\), with components of degree 3, 2, and 1. The component of lowest degree is \(-5x+7y\). Here, the equation of the tangent at the origin would be \(-5x+7y=0\). But we’re interested in more interesting cases.
For our unshifted bicuspid curve \(\left(x^2-1\right)\left(x-1\right)^2+\left(y^2-1\right)^2=0\), which can be expanded as \(x^4+y^4-2x^3-2y^2+2x=0\), the affine tangent cone is \(2x=0\), the vertical line shown in the graph above.
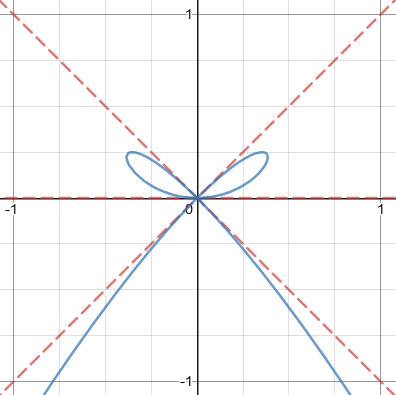
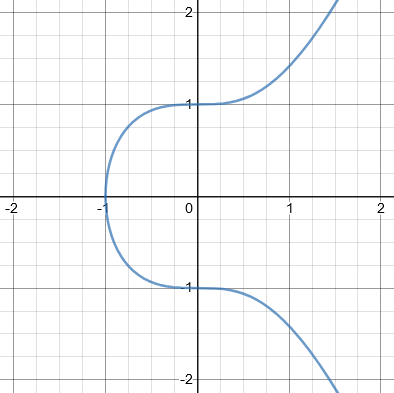
In your example, y² = x³ + x², we rewrite the equation as:
0 = (x² – y²) + x³
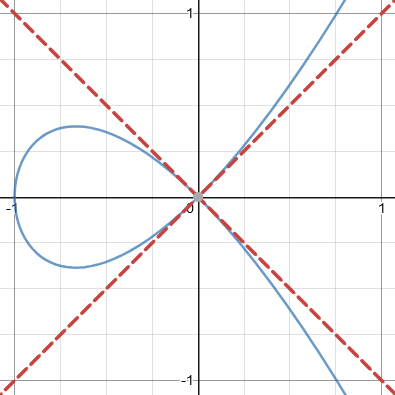
and the component of lowest degree is x² – y², which gives the equation of the tangent cone. The corresponding variety consists of the two red lines y = ±x; these are the two tangents at the origin:
The tangent cone is \(x^2-y^2=0\), which simplifies to \(y^2=x^2\), so that \(y=\pm x\). Just as a quadratic equation typically has two solutions, this equation consists of two lines. We’ll learn more about that later.
You may be wondering about the word “variety”. It’s just a word that covers curves, surfaces, and similar things of any dimension; by talking about algebraic varieties, we can talk about all those sorts of things at once. (You probably don’t want to read that link.)
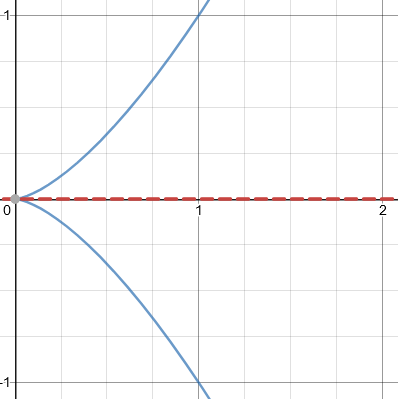
In general, the number of tangents at a singular point is at most equal to the degree of the affine cone. “At most” is important, because you can have a concept of multiplicity. For example, the curve y² = x³ has a cusp at the origin:
In this case, the affine tangent cone is y² = 0, which is simply the x-axis. You can consider this as a “double tangent”.
The name “tangent cone” comes from the fact that, since the equation is homogeneous by definition, if the point (a, b) is on the cone, then all points {(ka, kb) | k ∈ ℝ} are also on the cone.
So in this example, the two branches of the curve at the cusp share the same horizontal tangent, so although the degree is 2, there is only one tangent. Our shifted bicuspid above is similar.
You may have seen equations of literal cones; for example, the homogeneous equation \(z^2 = x^2+y^2\) represents a cone with its axis along the z-axis:
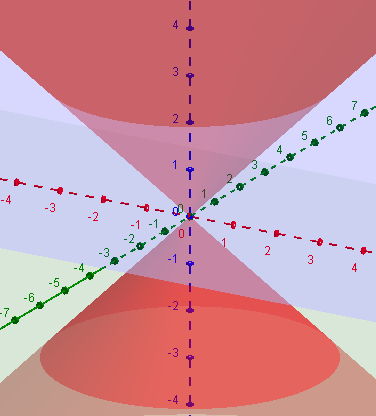
You can see some similarity between this 3-dimensional “cone” and the 2-dimensional “cone” represented by the tangents to our first equation.
Filling in the details
Andy replied,
Thank you for your answer!
Actually, I don’t understand well ‘the number of tangents at a singular point is at most equal to the degree of the affine cone.’
Could you explain this part in detail?
Doctor Jacques replied,
Hi Andy,
Let us start with the notations.
We have a curve given by a polynomial equation f(x, y) = 0, and that curve passes through the point (0, 0). We write the equation as:
f(x, y) = g(x, y) + h(x, y) = 0
where g(x, y) is the homogeneous component of lowest degree and h(x, y) contains all the terms of higher degree. Let us say that g(x, y) has degree n. We have n ≥ 1, because, as the curve contains (0, 0), f(x, y) has no constant term.
No tangents: n = 0
For example, the equation \(x^3-y^2+1=0\) has a degree-0 component 1 (a constant term), and is not satisfied by (0, 0). Its tangent cone would be \(1=0\), which is nonexistent:
So we aren’t going to see that happen. The component \(g(x,y)\) will always have at least degree 1.
One tangent: n = 1
g(x, y) = 0 is the equation of the affine tangent cone. If n = 1, g(x, y) = ax + by, and this is simply the equation of the tangent line.
For example, \(x^2-2y^3+2x-y=0\) has tangent cone \(2x-y=0\), or \(y=2x\), which means one tangent line:
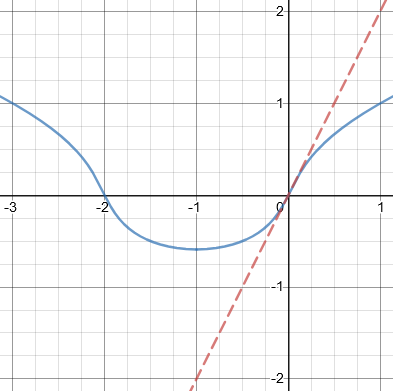
With one tangent, the origin here is not a singular point.
At most n tangents
If n > 1, we have a singular point, and there may be more than one tangent, or no tangent at all. Each tangent is described by a linear equation ax + by = 0, and (ax + by) is a factor of g(x, y). Obviously, if g(x, y) has degree n, it cannot have more than n linear factors: the number of tangent lines is at most n. This is what I meant with the statement in question.
This is like the fact that a polynomial equation may have any number of solutions up to its degree; a quadratic equation may have two solutions (corresponding to two distinct factors), or only 1 (if both factors are the same), or none (if it can’t be factored).
Exactly n tangents
If g(x, y) factors completely into distinct linear factors, there will be exactly n tangents, corresponding to these factors. This is what happened with the first example: we had g(x, y) = x² – y² = (x + y)(x – y), and the two tangents (shown in red on the graph) are given by the equations x + y = 0 and x – y = 0.
Recall that first graph:
For another example, consider the trifolium, with equation \(\left(x^2+y^2\right)^2=2\left(x^3-3xy^2\right)\):
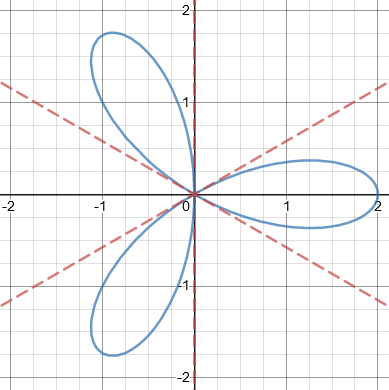
Expanding the equation to \(x^4+2x^2y^2+y^4-2x^3+6xy^2=0\), we see that the tangent cone is \(-2x^3+6xy^2=0\), with degree 3, which factors as \(2x(3y^2-x^2)=0\), so the tangents are \(x=0\) and \(\displaystyle y=\pm\frac{x}{\sqrt{3}}\).
Fewer than n tangents: repeated factors
On the other hand, you can have fewer than n tangents. Two things can happen.
First, you can have repeated factors. Those factors correspond to a single tangent. This is what happened in the second example: we had g(x, y) = y², but the equation y² = 0 is equivalent to y = 0 (the x axis). In this case, g(x, y) has degree 2, but there is only one tangent. In some sense, that tangent is counted twice.
Here is that second graph:
Fewer than n tangents: no factors
It may also happen that g(x, y) does not factor completely into linear factors. The irreducible factors of degree greater than 1 do not describe tangents. Consider, for example, the equation f(x, y) = x² + y² – y³:
Although this is not immediately obvious, the point (0, 0) belongs to the curve, as f(0, 0) = 0. This is an isolated point. In this case, the equation of the tangent cone is g(x, y) = x² + y² = 0, but the only solution of that equation is the single point x = y = 0. There are no tangents at the isolated point, which agrees with the intuition.
Note that, although x² + y² is irreducible over ℝ, over the complex numbers ℂ, we have the factorization x² + y² = (x + iy)(x – iy). In this case, you could say that there are two imaginary tangents; these are, of course, not visible on the graph.
You can also have both problems present in the same curve.
The correct statement is that the number of tangents is equal to the number of distinct linear factors of g(x, y); this is at most equal to the degree of g(x, y).
Andy was now satisfied. Clearly there is a lot more that could be said – that whole course in algebraic geometry that I never took, for example, not to mention that we haven’t proved anything here. But I hope this has whetted someone’s appetite for some graphing that goes far beyond the parabolas you learn in algebra class.
Your turn
Just for fun, let’s close with the knot curve, \(\left(x^2-1\right)^2=\left(y-1\right)^2\left(1+2y\right)\):
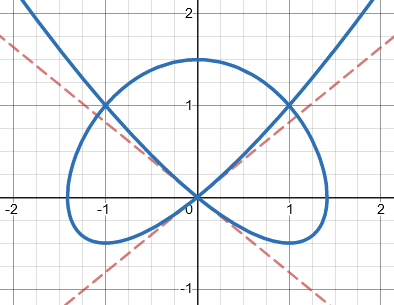
Can you find the tangent cone? How about if we shift it to \(x^2\left(x+2\right)^2=y^2\left(3+2y\right)\):
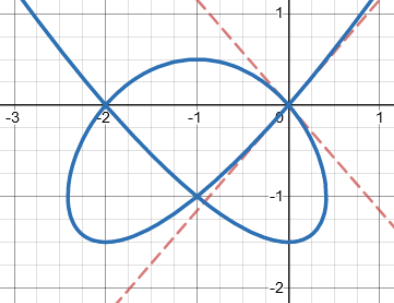

Pingback: Implicit Differentiation: Explanation, Examples, and a Surprise – The Math Doctors