Having recently helped some students (in person) with the rules of differentiation, I’m reminded to do so here, starting with the chain rule. It is easy to make this topic look harder than it really is; the two main ways to state the rule are often confusing, and different approaches fit different problems. We’ll try to untangle it.
Confused by u’s
We’ll start with a question from 1997:
Calculus Chain Rule I can't understand the chain rule. Every time I ask someone to explain it they use y's and u's, etc... could you give me the chain rule in easy terms, like how to do it, not just give me a formula like y=(U)^2? Thanks. Stu
A full statement of the chain rule tends to need lots of letters and tangled expressions. The short form Stu probably saw looks like $$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$ This says that if y is a function of u, and u is a function of x, then the derivative of the composite function y with respect to x is the product of the derivative of y with respect to u, and the derivative of u with respect to x.
What this says is simple, and almost intuitive. For example, suppose your altitude, h, is a function of the distance, s, along a road, and your distance along the road is a function of time, t. The road has a certain slope at any time, which is the rate of change of altitude with respect to distance, \(\frac{dh}{ds}\) meters up per meter forward; and your car has a certain speed, which is the rate of change of distance with respect to time, \(\frac{ds}{dt}\) meters per second. How fast are you going up? Every second you are moving \(\frac{ds}{dt}\) meters forward, and therefore \(\frac{dh}{ds}\cdot\frac{ds}{dt}\) meters up. That’s the derivative of the composite function \(h(t)\).
But often we don’t have a “u” in the problem, or any other variable – just one big expression like \(\cos(\tan(5x-3))\). Then what?
Doctor Scott answered:
Hi Stu! Good question. I was just skimming an excellent Calculus book written by Paul Foerster where this very question was addressed. His suggestion was that you should think of the chain rule as a process rather than a rule with a lot of du/dx and dy/dx's. So, here goes....
It’s like using muscle memory rather than written instructions.
Understanding composite functions
Remember that the chain rule is used to find the derivative of *compositions of functions* - that is, functions that have functions inside of them. For example, the function sin(x^2) can be thought of as a composition of two other functions, sin x and x^2, with the x^2 being INSIDE the sin function. Similarly, the function (x^2 - 5x + 8)^(1/2) is also a composition of two other functions, (x^2 - 5x + 8) and x^(1/2), with the first function being INSIDE the second. One more example? The function cos(tan(5x-3)) is the composition of three functions, 5x - 3 inside of tan x, inside of cos x. So the chain rule gets applied when there is some function INSIDE of another function.
We’ll be working all three of these examples.
We traditionally represent composite functions as boxes connected by “plumbing” (or, if you prefer, “links in a chain”, the reason for the term “chain rule”):
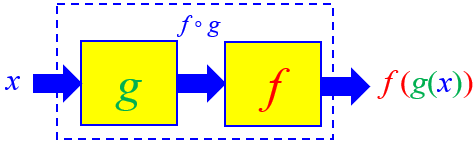
In particular, for our first example, we might think of it this way:

This sort of diagram has to be read backward; the first function named in the expression is the last one in line. I like to think of it this way instead, which reads more naturally:
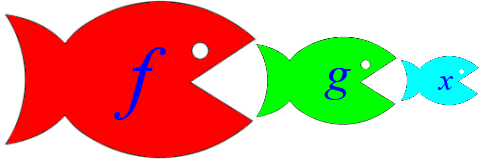
Each function/fish “eats” the one in front of it, producing “meat” that is eaten by the one behind. Then, we have fish inside fish:
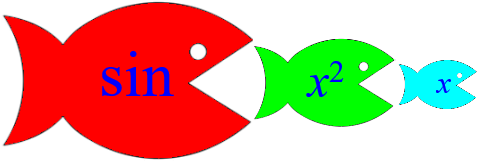
We can see this in the expression: $$\require{AMSmath}y=\boxed{\sin\left(\,\boxed{x^2\strut}\,\right)}$$
And we’ll apply the chain rule by following the “food chain” from the outside in.
Understanding the chain rule
The stuff that people have been telling you probably goes something like this: If y = sin(x^2), then we can write this function as the composition of y = sin u and u = x^2. (Again, notice that the x^2 is INSIDE of the sin function.) Then, dy/dx = dy/du * du/dx. So, we have dy/dx = cos u * 2x; but u = x^2, so we have dy/dx = 2x cos(x^2).
Here, u is just a temporary name we’re giving to the result of the inside function, like this:

This approach works fine when we are given named variables (as we’ll see later), but it gets in the way for problems like ours, where the function is written as one big expression.
But we don’t need names; we can just do it:
How about another way? Let's think of the chain rule as a process. The derivative of a composite function is the DERIVATIVE OF THE OUTSIDE FUNCTION TIMES the DERIVATIVE OF THE INSIDE FUNCTION. In practice, here's how it works. Consider y = sin(x^2). The outside function is a sine function; its derivative is cosine, so we have (so far) cos(x^2). Now, INSIDE the sine function is x^2. Its derivative is 2x, so now we have 2x cos(x^2). Notice that there is no other function "inside" the x^2, so we are done.
The key idea is that we have to keep the same thing inside the derivative that was inside the function itself. I like to think of it like this, putting a box (or at least imagining it) around the inside function and thinking of it as a single entity (as if it were a variable):
$$y=\boxed{\sin\left(\,\boxed{x^2\strut}\,\right)}$$
$$y’=\cos\left(\,\boxed{x^2\strut}\,\right)\cdot\boxed{x^2\strut}\,’=\cos\left(\,\boxed{x^2\strut}\,\right)\cdot2x$$
To differentiate “sine of something”, we multiply “cosine of something” by the derivative of “something”.
Let's look at a couple more examples: y = (x^2 - 5x + 8)^(1/2). The OUTSIDE FUNCTION is basically a power rule problem, so we have 0.5(x^2 - 5x + 8)^(-1/2) using the power rule. The INSIDE FUNCTION is x^2 - 5x + 8; its derivative is 2x - 5, so we have y' = (2x - 5)(.5)(x^2 - 5x + 8)^(-1/2).
Here we have
$$y=\boxed{\left(\,\boxed{x^2-5x+8\strut}\,\right)^{1/2}}$$
$$y’=\frac{1}{2}\left(\,\boxed{x^2-5x+8\strut}\,\right)^{-1/2}\cdot\boxed{x^2-5x+8\strut}\,’\\=\frac{1}{2}\left(\,\boxed{x^2-5x+8\strut}\,\right)^{-1/2}\cdot(2x-5)$$
This could also have been written as $$y=\boxed{\sqrt{\,\boxed{x^2-5x+8\strut}\,}\,}$$
$$y’=\frac{1}{2\sqrt{\,\boxed{x^2-5x+8\strut}\,}\,}\cdot\,\boxed{x^2-5x+8\strut}\,’\\=\frac{2x-5}{2\sqrt{\,\boxed{x^2-5x+8\strut}\,}\,}$$
I generally rewrite radicals as fractional powers, rather than memorize separate formulas for radicals.
y = cos(tan(5x-3)). The outermost function is a cosine, so its derivative is negative sine: -sin(tan(5x-3)). Inside the cosine is a tan function; its derivative is sec^2, so we now have sec^2 (5x-3) * (-sin(tan(5x-3)) Finally, inside of the tan function is 5x-3; its derivative is 5. So, FINALLY, we have 5 * sec^2 (5x-3) * (-sin(tan(5x-3)) Or, simplifying, we get y' = -5 sec^2 (5x-3) sin(tan(5x-3))
This has three layers (outside, middle, and inside):
$$y=\boxed{\cos\left(\,\boxed{\tan\left(\,\boxed{5x-3\strut}\,\right)}\,\right)}\\\\y’=-\sin\left(\,\boxed{\tan\left(\,\boxed{5x-3\strut}\,\right)}\,\right)\cdot\boxed{\tan\left(\,\boxed{5x-3\strut}\,\right)}\,’\\
=-\sin\left(\,\boxed{\tan\left(\,\boxed{5x-3\strut}\,\right)}\,\right)\cdot\sec^2\left(\,\boxed{5x-3\strut}\,\right)\cdot\boxed{5x-3\strut}\,’\\=-\sin\left(\,\boxed{\tan\left(\,\boxed{5x-3\strut}\,\right)}\,\right)\cdot\sec^2\left(\,\boxed{5x-3\strut}\,\right)\cdot5$$
So, it helps a lot to think of the chain rule as: The derivative of the outside TIMES the derivative of what's inside!
Confused by function notation
Consider this question from 1999, using another notation, which is technically more precise, but even more confusing to read:
Chain Rule Notation I'm trying to figure out these questions: Formula : (f◦g)'(x)= g'(x) · f'[g(x)] 1) f(x) = 2x+6 g(x) = 3x-4 (f◦g)'(x) = 3 · 2 = 6 I know that g'(x)= 3 but how about f'[g(x)]? How does 2 come about? I don't understand how it's done. 2) g(x) = 2x^2 + 5 h(x) = x^4 (g◦h)'(x) = 4x^3 · 4x^4 = 16x^7 It's the same here. I know how to differentiate h(x) but I got stuck on g'[h(x)]. How does 4x^4 come by? Please help me, Thanks.
The notation in the question means exactly what we’ve been doing. I prefer to write it in this order: $$(f\circ g)'(x)=f'(g(x))\cdot g'(x).$$ This means that the derivative of a composite function \(h(x)=(f\circ g)(x)=f(g(x))\) is the derivative of the outside function, f, applied to the inside function, g, times the derivative of the inside function, g.
The way I like to think about it, using the idea we saw above, is
$$\require{AMSsymbols}\boxed{f\left(\square\right)}\,’=f\,’\left(\square\right)\cdot\square\,’.$$
In the examples here, we are given the two functions separately (but with the same variable x, rather than an intermediate variable u). In the first question, functions were written as a single composite expression; in that form, respectively, these would be \(2(3x-4)+6\) and \(2(x^4)^2+5\). In this form, the inside functions could be marked like this: $$2\left(\,\boxed{3x-4\strut}\,\right)+6$$ and $$2\left(\,\boxed{x^4\strut}\,\right)^2+5$$
Doctor Mitteldorf answered, recommending the u formulation we avoided above:
Dear Eric, The chain rule can be taught in such a way that it's quite transparent, or it can be made utterly mysterious with bad notation. It looks as if you've been a victim of the latter. The chain rule is about taking the derivative of a function of a function. Instead of f being a function of x, we have f is a function of g, and g is a function of x. In this notation, the chain rule can be written: df/dx = df/dg · dg/dx It seems almost obvious when you write it that way. Just "cancel out" the dg's in the numerator and denominator.
In defense of the function notation form, that makes it explicit that the derivative of f is applied to \(g(x)\), not to x; and it emphasizes that the derivative is a new function f ‘, not a new variable. And this form is the most suitable for these problems, in which functions are named.
Doctor Mitteldorf here used g not only as a function name, but also as a variable representing its output. He did this, presumably, to avoid bringing in another variable (the u that was confusing above) to represent \(g(x)\). And many authors prefer to avoid the d notation precisely because it looks so “obvious”, as if you are just canceling in a fraction. (See What Derivative Notations Mean.) The latter notation is very useful as a reminder of this rule, but mathematicians are uncomfortable talking as if that is all there is to it. (See What Do dx and dy Mean?)
In your example (1), f(x) = 2x+6 g(x) = 3x-4 The teacher gave you a notation that's deliberately confusing. You have to remember that the x in these equations is a dummy variable. The top equation just says f is a function that takes its argument, multiplies it by 2, then adds 6. The x is there just as a placeholder. You can replace it with a or b or theta or phi and the equation says exactly the same thing.
This is important: The x‘s in the two function definitions will represent different numbers. So giving them different names helps to differentiate them (no pun intended).
But in this case, you want to replace it with g: f(g) = 2g+6 Is it obvious why I want to replace the x by a g? It's because f◦g means "f composed with g," or "the function f taken of the function g."
Distinguishing the variables called x is essential.
Coming back now to problem 1, let's do it two ways. First, we'll actually find f*g and differentiate it. Second, we'll use the chain rule. Then we'll be in a position to check that the two answers are the same. First, f(g) = 2g+6 g(x) = 3x-4 Substituting the second equation into the first, you have f(x) = 2(3x-4)+6 = 6x-2 It's obvious, then, that f'(x) = 6.
This process of expanding the composite function can be time-consuming; the chain rule is usually a time-saver. The point here is that it is not a necessity! It gives the same result as direct differentiation.
Second, we'll use the chain rule:
df/dx = df/dg · dg/dx
= 2 · 3 = 6
Hence, we get the same answer both ways.
This was a particularly simple example, where both derivatives are constant.
Powers of trig functions
Certain functions can make this harder. Here is a question from 1998:
Trigonometry and the Chain Rule I have three questions that have me stumped. I need to differentiate the following: y = 2 csc^3(sqrt(x)) y = x/2 - (sin(2x))/4 y = (1 - cos(x))/sin(x)
Doctor Santu answered, solving his own examples so Amanda could learn by doing her own homework:
Amanda: These all have to do with the Chain Rule. Here's the basic idea. Suppose: y = sin(x^3 + tan(x)). How do you find the derivative? Think of x^3 + tan x as a big BLOB. So we really need to find the derivative of: y = sin(BLOB) Well, the rule says that the derivative of sin(BLOB) is simply cos(BLOB) multiplied by the derivative of the BLOB itself. A word on notation: I'm going to write y' for the derivative of y (instead of dy/dx).
The BLOB idea is the same as my “something” or my boxes. I’ve been known to use the same word.
Now, in this case: y' = cos(x^3 + tan(x)) * (3x^2 + sec^2(x)) because BLOB is x^3 + tan(x), and the derivative of the BLOB is 3x^2 + sec^2(x).
Move the exponent
Now we come to something important: When we write a power of a trig function by putting an exponent on the function name (which, as I explained here, is a notation left over from before general function notation was introduced, as is permission to omit parentheses), we hide the fact that the power is the outside function, and the trig the inside:
Let's try another example: y = sin^3(x^3 + tan x) This is really: y = [ sin(x^3 + tan x) ]^3 Using our previous terminology, the derivative of (blob)^3 is simply: 3(blob)^2 * (the derivative of blob itself). In this case: y' = 3[sin(x^3 + tan(x))]^2 * (derivative of sin(x^3 + tan(x))) = 3[sin(x^3 + tan (x))]^2 * cos(x^3 + tan(x)) * (derivative of x^3 + tan(x)) = 3[sin(x^3 + tan(x))]^2 * cos(x^3 + tan(x)) * (3x^2 + sec^2(x))
By writing the exponent on the outside, we make it easier to see that the sine is the inside function.
In my formulation with boxes, this is $$y=\boxed{\,\left(\,\boxed{\sin\left(\,\boxed{x^3+\tan(x)}\,\right)}\,\right)^3}\\\\y’=3\left(\,\boxed{\sin\left(\,\boxed{x^3+\tan(x)}\,\right)}\,\right)^2\cdot\boxed{\sin\left(\,\boxed{x^3+\tan(x)}\,\right)}\,’\\
=3\left(\,\boxed{\sin\left(\,\boxed{x^3+\tan(x)}\,\right)}\,\right)^2\cdot\cos\left(\,\boxed{x^3+\tan(x)}\,\right)\cdot\boxed{x^3+\tan(x)}\,’\\=3\left(\,\boxed{\sin\left(\,\boxed{x^3+\tan(x)}\,\right)}\,\right)^2\cdot\cos\left(\,\boxed{x^3+\tan(x)}\,\right)\cdot\left(3x^2+\sec^2(x)\right)$$
Although the exponent is after the parentheses, we can see it clearly as on the outside, which wasn’t obvious originally.
Peeling the onion
In the chain rule, the basic idea is to peel the onion from the outside. You want to take the derivative of a function within a function within a function. You take the derivative of the outermost function relative to the stuff that's inside it, then multiply that by the derivative of the inside expression, relative to the expression inside the expression, and so on, all the way down to the tiniest little x all the way inside. (And some people even stick a "1" on at the end, because the derivative of an x is just 1. I think that's overdoing it a bit.) The Chain Rule needs quite a lot of imagination to see these formulas as expressions within expressions, and ideally you should have a friend sit by you and point out how to "peel the onion" layer by layer.
I’ve skipped a couple examples; he closed with an example five layers deep:
One final example:
y = sin(tan(sin^2(x^7 + 3x)))
y' = ...?
You must first take the derivative of sin (expression), relative to the expression that's inside. You multiply that by the derivative of the tan (inside expression). You multiply that by the derivative of [sin (x^7 + 3x)]^2, because sin^2 (x^7+3x) means [sin(x^7+3x)]^2. That, in turn, will contain the derivative of sin(x^7 + 3x), which in turn will contain the derivative of (x^7 + 3x), which is 7x^6 + 3.
It's important to put the proper expression inside the various partial expressions. So:
y' = cos(tan ...) * sec^2(sin ...) * 2[sin ...] * cos(x^7 + 3x) *
(7x^6 + 3)
You have to know what I have left out, and you must know how to put it in. I suggest you complete the derivative of that derivative just above, inserting all the expressions that would take the place of the ...s, then try the problems you're interested in. (All of us at Dr. Math had to practice these too.)
The function can be seen as $$y=\boxed{\sin\left(\,\boxed{\tan\left(\,\boxed{\left(\,\boxed{\sin\left(\,\boxed{x^7+3x\strut}\right)}\,\right)^2}\,\right)}\,\right)}$$
$$y’=\cos\left(\,\boxed{\tan\left(\,\boxed{\left(\,\boxed{\sin\left(\,\boxed{x^7+3x\strut}\right)}\,\right)^2}\,\right)}\,\right)\\\cdot\sec^2\left(\,\boxed{\left(\,\boxed{\sin\left(\,\boxed{x^7+3x\strut}\right)}\,\right)^2}\,\right)\\\cdot2\,\boxed{\sin\left(\,\boxed{x^7+3x\strut}\,\right)}\\\cdot\cos\left(\,\boxed{x^7+3x\strut}\,\right)\\\cdot\left(7x^6+3\strut\right)$$
Exponential functions
We’ll close with this, from 2004:
Chain Rule Applied to Exponential Functions At a time t hours after it was administered, the concentration of a drug in the body is f(t) = 27 e^(-0.14t) ng/ml. What is the concentration 4 hours after it was administered? At what rate is the concentration changing at that time? I got lost finding the derivative of the problem to find the rate of change. Part 1. f(4) = 27 e^(-0.14(4)) = 27e^(-0.56) = 15.42 ng/ml Part 2. Chain rule = f'(g(x)) x g'(x) = 27'(e^-0.56) x (e^-0.56) I get lost after that. I don't know if I am going in the right direction and I think the derivative of 27 = 0, so the whole first half of the problem would equal 0.
This is not really a hard application of the chain rule, but the notation is a little awkward. (A major error is in replacing t with 4 before differentiating, so there is no variable left!)
Doctor Mike answered:
Hi Brendan, The derivative of a constant times a function is just that constant, times the derivative of the function. So, the derivative of 27 e^(-.14t) is 27 times the derivative of e^(-0.14t) . So, let's just concentrate on the derivative of e^(-0.14t) and you can put it all together later. OK?
We can think of the 27 as representing an outer function \(a(x)=27x\), whose derivative is 27; but it’s easier just to let it pass through the process.
People often have problems with the Chain Rule applied to exponentials, because of not being clear of what is the "outside" function and what is the "inside" function. That's why I like to use the notation exp(x) in place of the notation e^x when we do problems like this. Also, let's give a function name "h" to what is in your original exponent. That is, define it like h(t) = -0.14t . Then, e^(-0.14t) can be written as exp( h(t) ) which clearly shows that the exponential is the outside function, and what we have called "h" is the inside function.
So we have the function \(f(t)=\exp(h(t))\), where \(\exp(x)=e^x\) and \(h(t)=-0.14t\).
What do we do with this now? To use the Chain Rule you have to know how to differentiate both functions that are involved. The exponential function is its own derivative. exp'(t) = exp(t). You should have seen this already. For the other one, h'(t) = -0.14 . That you should have seen a long time ago. Right? So, to use the Chain Rule on exp( h(t) ) you get exp'( h(t) ) * h'(t) which is exp( h(t) ) * (-0.14) . In this last expression, exp( h(t) ) is the derivative of the outside function evaluated at the inside function, and (-0.14) is the derivative of the inside function.
We don’t have to do this renaming, as long as we see the exponent as the inside function: $$f(t)=e^{\boxed{-0.14t}}$$ If you find the “exp” function helpful, use it: $$f(t)=\exp\left(\,{\boxed{-0.14t}}\,\right)$$
The general notation for differentiating f(t) = g( h(t) ) with the C.R. is simply f'(t) = g'( h(t) ) * g'(t) . If you spend some time to get your function expressed in that way, then the rest will be easier.
Carrying out the process, we have $$\boxed{27\boxed{e^{\boxed{-0.14t}}}}’\\=27\boxed{e^{\boxed{-0.14t}}}’\\=27e^{\boxed{-0.14t}}\cdot\boxed{-0.14t}’\\=27e^{\boxed{-0.14t}}\cdot(-0.14)$$

Pingback: How to Think About the Product and Quotient Rules – The Math Doctors
Pingback: Implicit Differentiation: What to Do When It’s “Wrong” – The Math Doctors
Pingback: Proving the Chain Rule: Details Matter – The Math Doctors