I am always interested in problems that can be solved in different ways, particularly because this can give a student a chance to be creative, as well as learning from experience that you don’t have to do it “the teacher’s way”. Here we’ll use trigonometry, and two different ways to add lines to a figure for a geometrical solution.
The question is from Amia, in mid-November:
Hi Dr math,
I need hint to solve this question:
Thank you in advance.
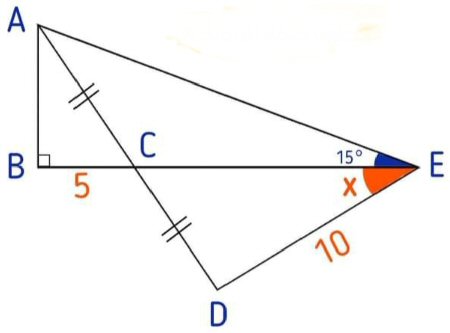
Clearly we are to find the value of angle x; all the required information is indicated in the picture: AB is perpendicular to BE; point C, on BE, bisects AD; the lengths of BC and DE are, respectively, 5 and 10; and the measure of \(\angleAEB\) is 15°.
A trigonometric solution
I answered first, giving a hint and an overall approach:
Hi, Amia.
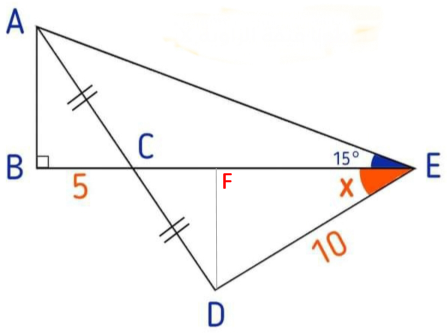
I used trig, with the auxiliary line DF shown:
The answer is a very nice number, so there may well be a geometrical solution.
But be careful not to assume angle CDE is a right angle; it isn’t.
The warning is related to what I said in What Role Should a Figure Play in a Proof?
Since we’ll be pursuing geometrical solutions, I’ll show my work here (though it will be a spoiler as to the actual answer).
I’ve constructed F as the foot of the perpendicular from D to BE. This results in similar right triangles \(\triangle ABC\) and \(\triangle DFC\); so the length of CF is 5, and \(|AB|=|DF|\).
From right triangle \(\triangle DFE\), we find that $$|DF|=10\sin(x)\\|EF|=10\cos(x)$$
Therefore, $$|BE|=10+10\cos(x)$$
From right triangle \(\triangle ABE\), $$|AB|=|BE|\tan(15^\circ)=(10+10\cos(x))\tan(15^\circ)$$
But since \(|AB|=|DF|\), we see that $$(10+10\cos(x))\tan(15^\circ)=10\sin(x)$$
Dividing by 10, and temporarily letting \(t=\tan(15^\circ)\) (though we could actually calculate its exact value if we wanted, as half of 30°), we have the equation $$(1+\cos(x))t=\sin(x)$$
Expressing \(\sin(x)\) as \(\sqrt{1-\cos^2(x)}\), this becomes $$t+t\cos(x)=\sqrt{1-\cos^2(x)}$$
Temporarily letting \(c=\cos(x)\), and squaring both sides, we have a quadratic equation in c: $$(tc+t)^2=1-c^2$$ Now we just have to solve this for c: $$t^2c^2+2t^2c+t^2=1-c^2\\(t^2+1)c^2+(2t^2)c+(t^2-1)=0$$
Applying the quadratic formula (though we’ll see we could actually have factored this!), $$c=\frac{-2t^2\pm\sqrt{4t^4-4(t^2+1)(t^2-1)}}{2(t^2+1)}\\=\frac{-2t^2\pm\sqrt{4t^4-4t^4+4}}{2(t^2+1)}\\=\frac{-2t^2\pm2}{2(t^2+1)}\\=\left\{\begin{matrix}\frac{-2t^2+2}{2(t^2+1)}=\frac{1-t^2}{1+t^2}\\\frac{-2t^2-2}{2(t^2+1)}=-1\end{matrix}\right.$$
But if \(\cos(x)=-1\), then \(x=180^\circ\), which is clearly an invalid solution; while the other solution is $$\cos(x)=\frac{1-\tan^2(15^\circ)}{1+\tan^2(15^\circ)}=\frac{1-\tan^2(15^\circ)}{\sec^2(15^\circ)}=\cos^2(15^\circ)-\sin^2(15^\circ)=\cos(2\cdot15^\circ)=\cos(30^\circ)$$
Therefore, \(x=30^\circ\).
That is the “very nice number” I mentioned.
If I had given this answer, others might have planned a geometrical solution expecting to double the given angle; as it is, we’ll see two independent solutions based only on my hint (or not).
A geometrical hint
An hour later, Doctor Rick made a suggestion:
Hi, Amia, I’m joining in.
I liked the line Doctor Peterson constructed, DF perpendicular to BE, because (1) it creates a pair of congruent triangles, which are always good to see; and (2) it creates a second line segment of length 10.
It would be very nice to have two sides of length 10 in the same triangle! I found a way to construct such a triangle. There may be a more elegant solution (I ended up constructing a total of four line segments), but this one worked for me!
We’ll see his solution below.
First geometrical solution
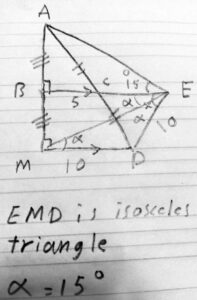
Two days later, Amia showed us a solution using a different construction:
Here is my attempt:
This is not explained, but the markings make the intention clear.
I replied:
I like it.
You’ve presumably found the answer, though you didn’t state it, and the drawing suggests that you could prove it if asked. I imagine this is either Doctor Rick’s solution, or the more elegant one he expected to exist. (It’s also the result I got by my utterly inelegant trigonometry.)
Amia has first constructed point M, by reflecting A in line AE, so that \(BM\perp BE\) and \(BM\cong AB\):
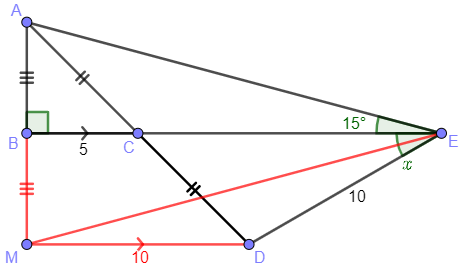
We see that triangles \(\triangle ABC\) and \(\triangle AMD\) are similar, by SAS, with similarity ratio (scale factor) 1:2, so that \(|MD|=10\). and \(MD\parallel BC\).
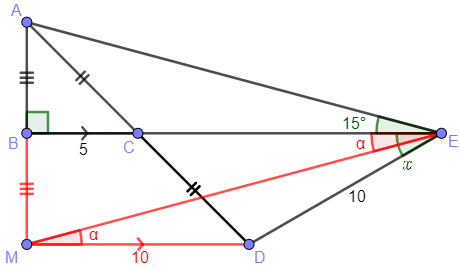
Since ME is a transversal of these parallel lines, we have a pair of alternate interior angles, \(\triangle DME=\triangle BEM=\alpha\):
But since triangle \(\triangle MDE\) has equal sides \(|MD|=|DE|=10\), it is isosceles, and its base angles \(\angle DME\) and \(\angle DEM\) are congruent (again, \(\alpha\)):
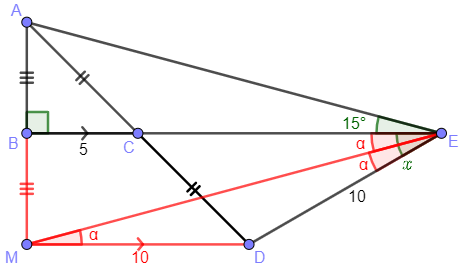
Finally, right triangles \(\triangle ABE\) and \(\triangle MBE\) are congruent, so angles \(\angle AEB\) and \(\angle MEB\) are congruent. This implies that \(\alpha=15^\circ\), and \(x=2\alpha=2(15^\circ)=30^\circ\).
Second geometrical solution
Now Doctor Rick finished:
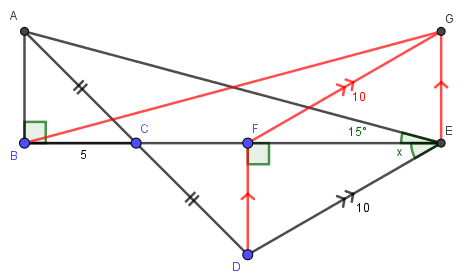
My proof was different but related to yours; I think yours is nicer. Here is my figure:
ΔBEG is congruent to ΔEBA, and triangle BFG is isosceles, so that ∠GFE = 2∠GBE; but ∠FED = ∠GFE, and ∠GBE = ∠AEB = 15°. Thus ∠FED = x = 30°.
As I interpret this, he has constructed G so that EG is parallel and congruent to DF; as a result, FG is parallel and congruent to DE, which has length 10. Since BF also has length 10, triangle \(\triangle BFG\) is isosceles. And because BA is similarly parallel and congruent to DF, angles \(\angle GBE\) and \(\angle AEB\) are congruent, namely 15°. The rest follows, after using the fact that exterior angle \(\angle EFG\) is the sum of the other interior angles \(\angle FBG+\angle FGB\).:
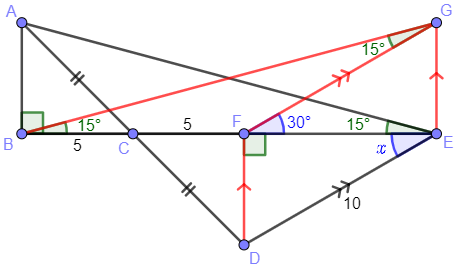
This example illustrates the value of a carefully chosen auxiliary line, while also showing that there can be more than one such line. (The two proofs have a lot in common.)
I imagine there are other geometrical solutions, too. Ideas are welcome.